基于FTM方法的二维Kelvin-Helmholtz不稳定性数值模拟

2018-09-06，，，，

计算力学学报 2018年4期

，，，，

(南昌大学机电工程学院，南昌 330031)

1 引言

K-H(Kelvin-Helmholtz instability)[1]不稳定性是自由剪切流的无粘不稳定性。一般认为，不互溶的混合流体中，上层流体与下层流体间的速度差异足够大时，界面上存在的微小扰动会使界面变形，出现Kelvin-Helmholtz不稳定性。

K-H不稳定性的数值研究一直是计算流体力学的经典问题。晶格-玻尔兹曼方法LBM[2-5]LBM(Lattice -Boltzmann Method)能通过耦合分子间的相互作用正确地模拟界面的运动，其与界面运动和瑞利-泰勒不稳定性[6]的研究类似，对于不混溶的两相混合层的研究，LBM多相流模拟有良好的前景。

Lee等[7]用具有高分辨率和高精度的相场法(Phase-field Method)模拟多组分流体的K-H不稳定性，并研究了韦伯数、密度比和速度差对K-H不稳定性的影响。相场法的优点在于无需进行显性界面追踪，并且能自动处理多相物理界面拓扑结构的改变，计算的时间步长也可以更大，在处理多组分流体时有独特优势，然而传统相场法计算的精度却有待提高。

Shadloo等[8]用平滑颗粒流体动力学(SPH)方法模拟K-H不稳定性，并研究了理查德森数和密度比的影响，发现K-H不稳定性的增长主要受理查德森数的影响，而不仅是稳定力的作用。Tryggvason等[9]利用涡片单元法[10-12]研究了相对薄的涡量层K-H不稳定性的大振幅阶段。在对非常薄的涡量层K-H不稳定性的大振幅演化求解中，将无粘性、正规化的涡片单元模型和全粘性纳维斯托克斯求解方案进行比较。结果表明，非粘性模型的零正规化标度的极限、极限的高雷诺数和较小的初始厚度的粘性计算基本一致。

FTM[13-14]通过显示跟踪相分界面，具有以高精度高分辨率捕捉界面结构拓扑变化的优点。本文利用该优点模拟了二维下流体的K-H不稳定性，通过选取不同的速度梯度层厚度、速度差、边界条件和理查德森数研究了K-H不稳定性的界面形态演化的过程。此外，将Neumann边界条件和Dirichlet边界条件下的涡量分布进行对比，从而判断两种边界条件对涡量分布的影响程度。

2 数值方法和数学模型

2.1 控制方程

使用显式的有限差分方法求解控制方程，二维不可压缩流动的动量方程为

σκδ(x-xf)

(1)

式中xf为界面位置,ρ和μ分别为非连续的密度场和黏度场,κ为平均曲率,δ只有在界面上时才不为0,其他参数遵循习惯约定。

2.2 密度场和黏度场重构

不互溶、不可压缩的流体在界面两侧保持各自的特性，因此在界面上存在物性阶跃。FTM算法中，通过赋予界面一定厚度的过渡区，让流体的特性在这个区域内实现平滑过渡。当界面移动时，界面上的密度和黏度分布随之发生变化，故引入Heaviside函数[15]来表征这种变化，

(2)

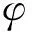
(3)

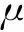
(4)

2.3 界面追踪

界面的运动通常是与固定网格结合在一起，采用双线性插值法实现界面与网格间的信息交流，其表达式为

(5)

2.4 表面张力

界面上表面张力的计算表达式为

Fσ=σκnδ(x-xf)

(6)

式中δ(x-xf)为狄拉克函数，在界面上为1，其余都为0。

取单位面元上的表面张力为研究对象，对于二维流动有

κn=∂t/∂s

(7)

因此得到单位界面元上的表面张力为

(8)

式中t为界面上的切向量，s为界面元，l为界面上的节点。

2.5 数值模型

h(x,y;a,y0,ampl,ε)= tanh{[y-y0-

ampl*sin(aπx)]/ε}

(9)

扰动形式为由函数A=A0e- i k x +n t赋予界面一个初始扰动，其中k为波数，t为时间，当考虑重力和表面张力时，根据文献[1]的结果，可表示为

(10)

式中若等号右侧第二项的结果为非负数，扰动稳定，否则，扰动将会随时间而增长。当扰动不稳定时，等号右侧第二项可以写为

(11)

经过简单的数学变换，可以得到式(12)，Ri为理查德森数，在物理学中，理查德森数用于表征流体势能与其动能的比值，势能包含了重力项和表面张力项。

(12)

图1 流体布局示意图

Fig.1 Schematic on fluid layout

(13)

(14)

3 数值模拟结果及分析

3.1速度梯度层厚度的影响

在不考虑速度梯度层的厚度时，上下两种流体的速度相等，即|u1|=|u2|，实际过程中界面交界处存在速度的过渡区，从而会产生速度梯度层，速度梯度层的厚度会影响K-H不稳定性的发展，如图2所示。ε=0.10时，受速度梯度层的影响，界面向内发展的趋势明显受到抑制，更多的是向右发展，涡量分布也比较散。随着ε减小，速度梯度层变薄，对K-H不稳定性的影响减弱，K-H不稳定性发生的时间也提前。当ε≤0.04时，界面形态和涡量分布已经非常相似，由速度梯度层厚度造成的影响基本可以忽略。因此本文在余下的数值模拟中，均选取ε=0.02时的速度梯度层厚度为基准。

3.2 速度差的影响

在不考虑切向剪切力的情况下，界面平衡时，剪切力和表面张力满足

μ(∂u/∂y)=σκ

(15)

式中μ为流体粘度,κ为表面界面曲率，在本节中初始条件为

u(x,y)=h(x,y;2,0.5,0.01,0.02)

v(x,y)=0

(16)

不考虑梯度层的厚度，上下两种流体的速度大小相同，使用2×|u|来衡量速度梯度的大小。从式(14)可知，当界面处的速度梯度不足以破坏表面张力维持的稳定时，界面的稳定将不会打破。图3分别为t=2.0 s时刻速度梯度为2×|0.4u|， 2×|0.8u|， 2×|1.2u|和2×|1.6u|四种情况下界面的形态(a,b,c和d)和流场涡量(a1，b1，c1和d1)分布。可以看出，速度差越大，界面上的剪切力越大，当剪切力的作用大于表面张力和重力的作用时，界面上的扰动就会发展为K-H不稳定性。对比图3的四种情况可以发现，界面的不稳定发生的时间会因为速度梯度的增加而提前，并且同一时刻的界面变形及涡量的扩散强度均会随着速度梯度的增大而增大。

3.3 边界条件的影响

对比两种边界条件的影响，得到图4的界面形态的演化和图5涡量随时间的变化，两种边界条件的初始条件均如式(16)所示。

K-H不稳定性是由界面上的扰动引起的，一般有三个发展方向，分别为向上、向内和向右(由U1的速度方向决定)，而最明显的是向内发展，图4 的结果也印证了这点。两种边界条件下，尽管初始条件相同，同一时刻Neumann边界下界面的变形和卷曲程度明显比Dirichlet边界下的剧烈，随着界面上扰动的增长，这个现象愈加明显。Neumann边界条件下，K-H不稳定性非常明显，表现为界面向内卷的圈数更多，卷起的液膜更薄，而在Dirichlet边内卷起的圈数明显减少，卷起的液膜也变厚。受边界条件的影响，抑制最明显的是界面向内发展的过程，然而界面形态的演化过程却非常相似，这表明边界条件并不能完全抑制K-H不稳定性的发展。

图2t=2.0 s时刻不同速度梯度层厚度的界面形态和涡量分布

Fig.2 Interface pattern and vorticity distribution with different thickness of velocity gradient layers whent=2.0 s

不同边界条件的涡量随时间的变化如图5所示，初始时刻的涡量均匀分布在两种流体的界面上，在方向相反的初始速度的推动下，上层流体主动向下运动，下层流体主动向上运动，涡量逐渐卷入中心，两种流体互相渗透形成漩涡，随着涡量在中心的堆积，界面开始变得陡峭，扰动的振幅也逐渐增长，界面形态的转变与涡量变化一致。Neumann边界条件下，涡量向两边扩散得比较少，在方向相反的初始速度作用下迅速向中心聚集形成漩涡，当漩涡达到一定强度时，涡量才开始往两边扩散；而在Dirichlet边界条件下，涡量在K-H不稳定性发展的初期已经开始往两边扩散，因此界面中心形成的漩涡强度更弱，使得K-H不稳定性向内的发展受到很大影响。