基于BP神经网络的井筒连续流量计启动速度预测

陈科贵,毛晨飞,董军,陈愿愿,黄长兵,王小准

(1.西南石油大学地球科学与技术学院,四川 成都 610500;2.中国石油集团测井有限公司华北分公司,河北 任丘 062550;3.中国石油集团川庆钻探工程有限公司地球物理勘探公司,四川 成都 610213;4.中原油田勘探开发研究院,河南 郑州 450000;5.中国石油集团测井有限公司长庆分公司,陕西 西安 710100)

0 引 言

在油田的长期开发过程中,储层状态往往会产生较大的变化,油气水的分布状况会变得愈加复杂[1]。为了更加准确地分析判断油田产液剖面形状,必须要进行产出剖面测量[2]。在产出剖面测量中,连续涡轮流量计由于其结构简单、体积较小、上限排量高的优点得到了广泛地应用[3-4]。一般情况下,首先获取电缆上下移动时的测井速度和与之对应的涡轮流量计响应数据,再利用最小二乘法或最优化法确定涡轮流量计启动速度。2005年,李鹏举等[5]对连续涡轮流量计的响应方程进行了深入研究,并提出了2种连续涡轮流量计的定量解释方法。在依赖于响应方程的流体视速度的求取方法中,涡轮启动速度的精确性起着至关重要的作用[6]。2007年,陈科贵等[7]对产液剖面流体视速度求取方法的适用条件进行了研究。根据实际应用情况,通常采用上下混合测量最小二乘法和上下分测刻度法确定涡轮启动速度[8]。在中、高产油水两相井中上下混合测量最小二乘法和上下分测刻度法均适用,而在低产油水两相井中,上下分测刻度法更为适用[7]。涡轮启动速度受到流量、流体黏度、混合流体密度以及涡轮流量计顶尖与轴承摩阻特性等因素的综合影响[9-10]。

上述2种求取涡轮启动速度的方法在实际应用中由于忽略了这些因素的影响,其求取的涡轮启动速度存在较大误差,且会出现一些异常情况[11]。降低误差且对这些异常启动速度进行预测校正成为准确求取流体视速度的关键问题。

本文通过分析连续流量计涡轮启动速度与各影响因素之间的关系,以××油田10口井的大量测量数据为基础,应用BP神经网络[12-14]建立了综合考虑流量、流体黏度和混合流体密度等因素的连续流量计涡轮启动速度预测模型。

1 连续流量计启动速度的影响因素

连续流量计的实际应用中,涡轮转动必须满足的条件是涡轮的驱动力矩大于轴承的静摩擦阻力距[15]。将连续流量计的涡轮克服静摩擦阻力距转动时,通过涡轮流通截面的最小流量值称为该连续流量计的启动流量阈值Qmin,此时通过涡轮流通截面的流体所具有的平均速度称为启动速度vmin[16]。根据连续流量计的基本原理,并进行分析推导后可知,在涡轮启动时,其启动速度为[7]

(1)

式中,vmin为电缆速度为0时连续流量计的涡轮启动速度;Qmin为连续流量计涡轮的启动流量阈值;T2为机械摩擦阻力矩;ρ为流体密度;C1为与仪器结构相关的常数;A为流道面积。

从式(1)中可以得出,涡轮的启动速度受到井筒内流体流量、混合流体密度和机械摩擦阻力矩的影响。虽然从连续流量计的工作原理中已推导出涡轮启动速度的计算公式,但公式中的机械摩擦阻力矩T2难以得到,因此无法通过式(1)定量求解启动速度和流量、密度和机械摩擦阻力矩之间的响应关系。

在前人对连续流量计涡轮受到的摩擦阻力矩进行的研究分析的基础上可知,涡轮摩擦阻力矩主要由流体黏滞性摩擦阻力矩T1和机械摩擦阻力矩T2组成[16]。其表达式为

T1=C1ηQ+C2ρQ2

(2)

式中,C1和C2为与流型有关的比例常数;η为流体的黏度;ρ为混合流体的密度;Q为流量。

(3)

式中,T0为无负荷时的机械摩擦阻力矩;μ为轴承的摩擦系数;d0为轴承中滚珠的直径;α为涡轮叶片的倾斜角度。

从式(2)和式(3)中可知,机械摩擦阻力矩T2是流体黏度和混合流体密度的函数。因此可以通过研究流量、流体黏度、混合流体密度和启动速度之间的映射关系准确地求解涡轮启动速度。

2 BP神经网络基本原理

BP神经网络类似于一个非线性原件[17-19],其具有多个输入节点,在经由隐含层加权计算后,将误差反向传播,对非线性结构不断进行优化,从而将复杂的输入参数和输出参数之间的非线性映射关系简化,最终实现输入参数和输出参数之间的完美映射[20]。该网络的运行过程主要分为3部分,信号输入后逐层加权计算并向前传输,将输出值与期望值对比计算误差,最后再将误差逐层反馈调整计算权值[21-22]。信号向前传输的过程中,每个输入信号都要经过隐含层的加权计算。逐层处理时,每层的神经元输出结果只会受到上一层神经元输出结果的影响。输出值与期望值对比后的误差如果大于设置的目标误差,则将误差再逐层反馈,根据反馈的误差对网络权值进行不断的调整,使误差不断减小[23],直到误差小于设置的目标误差或达到最大运算次数,则网络运行结束[24]。BP神经网络的拓扑结构如图1所示。

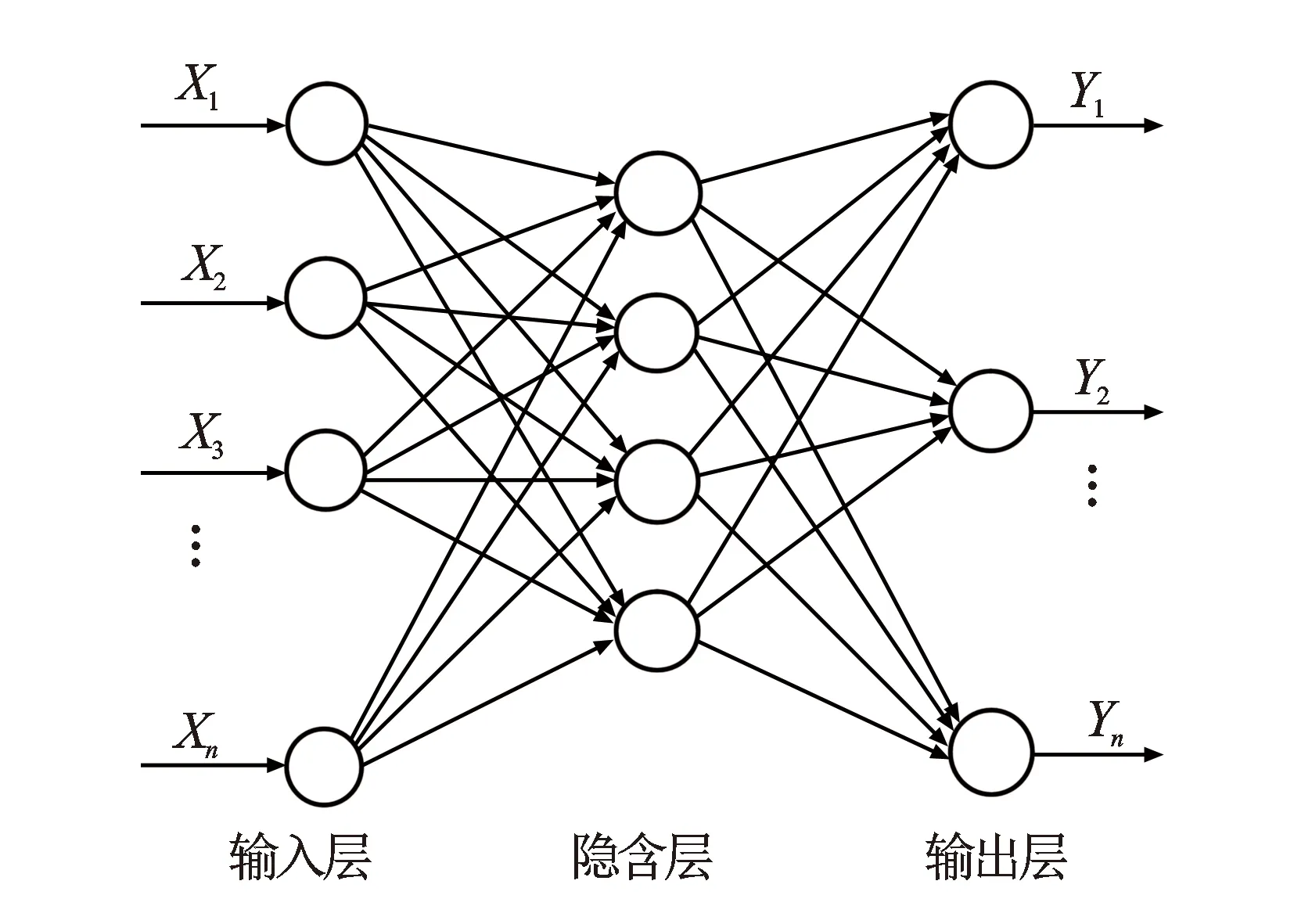
图1 BP神经网络拓扑结构图

3 连续流量计启动速度预测模型

将BP神经网络用于非线性函数拟合时,具体过程可以分为建立网络结构、训练网络单元和预测结果对比3步[25]。本文利用3层神经网络构建连续流量计涡轮启动速度预测模型,将流量、流体黏度和混合流体密度作为输入层的神经元节点,将连续流量计涡轮启动速度作为输出层的神经元节点,隐含层节点数设置为8,对BP神经网络进行训练并进行启动速度的预测。BP神经网络启动速度预测模型的结构如图2所示。

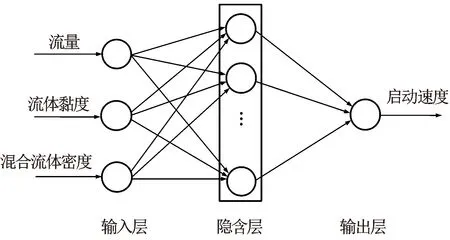
图2 启动速度预测神经网络结构图

3.1 样本数据

××油田处于低产量中含水开发阶段,研究区块的井普遍存在脱气现象,导致井筒内流型变化复杂,在井筒内流体流型改变的同时,流体的黏度和混合流体的密度将伴随流型的改变而产生相应的变化,并且井筒内流量较低,涡轮转速较小。不同测速、不同流量的测量条件下,仪器响应相关性较差,常常为非稳态响应。根据流量测井资料,采用上下分测刻度法求取流体视速度时,启动速度异常和截距异常现象往往会同时且频繁出现[7]。本文以××油田10口井中的50组流量测井资料为依据,对BP神经网络进行训练与预测,进而对启动速度进行预测,最终实现对异常启动速度的校正。

3.2 样本数据训练与预测

本文BP神经网络预测模型的构建主要用到newff函数(BP神经网络参数设置函数)、train函数(BP神经网络训练函数)和sim函数(BP神经网络预测函数)。为防止数据本身的差异对计算结果造成影响,需要对样本数据进行归一化处理,因此在输入样本数据时还调用了归一化函数mapminmax,其数据分布在[-1～1]之间。网络训练的目标误差为0.000 1,将学习率设为0.01,限定最大循环次数为500次,BP神经网络预测模型的结构为3×8×1。为了使样本的输入顺序对预测结果不会产生影响,本文从表1中的50组输入数据中随机抽取40组数据作为网络训练数据,剩余的10组数据作为网络测试数据。

将BP神经网络参数设置完毕后,根据表1对其进行训练,训练收敛之后,对该神经网络模型进行分析。总体拟合优度为0.917,该模型具有很好的拟合优度(见图3)。

BP神经网络预测模型经过训练后,将该模型所得的实际输出与期望输出进行对比,相对误差见图4。该模型预测结果的最大相对误差为2.0%。以上结果说明,针对连续流量计涡轮启动速度预测所建立的BP神经网络模型可以很好地反映出连续流量计启动速度和流量、流体黏度以及混合流体密度之间的内在联系和相关规律。

由图4可知,通过BP神经网络所得到的连续流量计启动速度具有很高的可靠性,且该方法具有很强的实用性。对于不同研究区块内,不同条件下的流量测井,只需根据研究区内各种条件下的实际观测值对BP神经网络预测模型进行重新训练,便可建立适用于各种条件下的预测模型来预测连续流量计启动速度,并且预测结果具有很高的准确性,也可对其他方法求取的异常启动速度进行有效校正。

综上所述,BP神经网络在解决连续流量计启动速度预测的问题时,具有很强的可行性和实用性。在实际的流量测井解释中,可根据实际测量到的产量,再与流体黏度和混合流体密度相结合,通过训练好的BP神经网络预测模型,对整个流量层的启动速度进行预测并校正异常启动速度,最终提高流体视速度的求解精度。

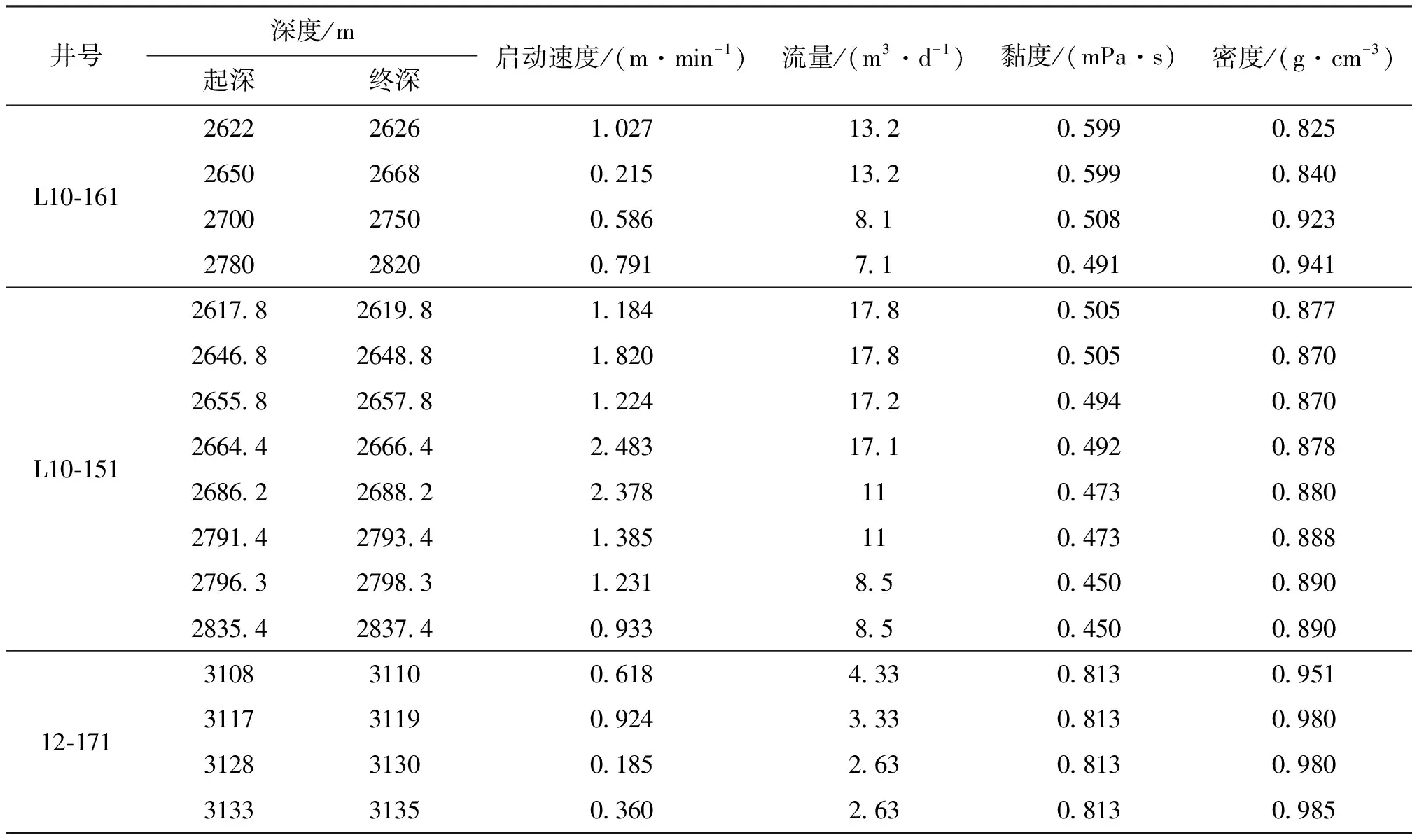
表1 样本数据(部分)

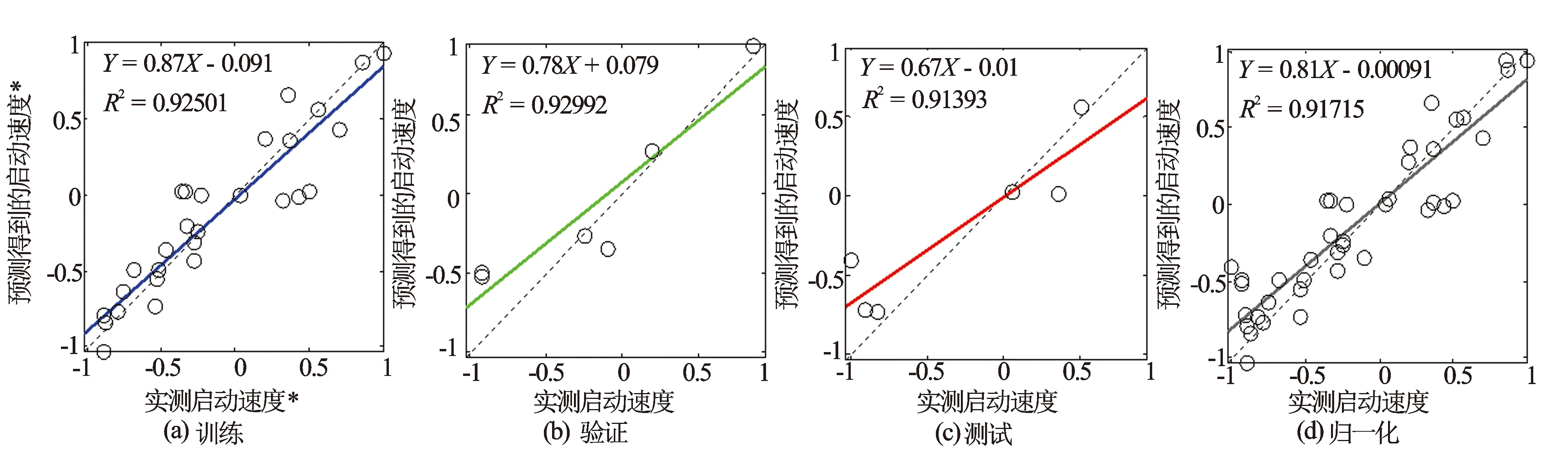
图3 BP神经网络回归分析图*数据归一化处理后分布在[-1～1]之间

图4 连续流量计启动速度预测结果误差百分比

4 结 论

(1) 对连续流量计启动速度的主要影响因素为流量、流体黏度和混合流体密度等,并以此为基础建立了预测连续流量计涡轮启动速度的BP神经网络模型。

(2) 用BP神经网络解决连续流量计启动速度的预测,经验证是可行且可靠的。BP神经网络连续流量计启动速度预测模型的总拟合优度为0.917,最大相对误差为2.0%。这说明该预测模型对连续流量计启动速度的预测具有较高精度。使产液剖面的解释更加准确,可进一步提高油田采收率。

(3) 油田实测的地面流量、流体黏度和混合流体密度是建立BP神经网络预测模型的基础,对于不同研究区块,不同测量条件,可应用不同区块的实测值建立相应的BP神经网络预测模型,该方法具有很强的适用性。