分数阶Willis环脑迟发性动脉瘤时滞系统混沌分析∗
2018-09-06高飞胡道楠童恒庆王传美
高飞 胡道楠 童恒庆 王传美
(武汉理工大学理学院,武汉 430070)
(2018年2月2日收到;2018年4月16日收到修改稿)
1 引 言
Willis环脑动脉血管瘤是一种高致死率疾病[1],治疗过程中有可能会因基于植入血流导向装置[2−4]和支架联合弹簧圈[5]等治疗方式引起不明原因的迟发性动脉瘤破裂[6].动脉瘤的延迟性破裂危害巨大,一旦出现将严重危及病人生命.
生理上动脉瘤破裂与否与血流速度密切相关,故以血流速度为主要研究对象,以血流动力学相关原理建立的脑动脉血管瘤动力学模型系统[7−10]在临床及理论研究中发挥了重要作用.动脉瘤破裂表现为血流速度的巨大改变,亦即出现“尖峰”,虽然不是所有尖峰都会引起动脉瘤破裂,但是没有尖峰意味着血流流速稳定,病情稳定,系统表现为稳定状态;反之,存在尖峰的系统则表示为混沌状态.
最初的Willis环脑动脉血管瘤系统(Willis aneurysm system,WAS)由Austin[11]利用实验模拟得到,现有研究多以整数阶阻尼项脑动脉瘤系统[12]为基本模板,对其进行混沌理论分析[13−15]和模型改进[16,17].在模型改进方面,近年来主要有基于药物的整数阶WAS模型[16]和基于血液软物质性[18]、黏弹性[19]特性的分数阶WAS[17]等.但是,对于不明原因引起的迟发性动脉瘤破裂,也就是系统中尖峰延迟出现的情况(即“时滞”),上述模型并不能给出合理的描述和解释.
近年来,分数阶微积分作为一种有用的数学工具被广泛应用于生物及医学方面[20,21];而时滞一直存在于现实中并影响着系统的动态,故分数阶时滞系统引起了学者们的广泛研究和关注[22,23].时滞加入后,会破坏原来系统的稳定性并影响着系统动力学行为,使系统变得更加复杂,而临床上脑动脉瘤里血管内情况亦是错综复杂.现有WAS的相关机理及理论滞后于临床现实,因此,研究带有时滞的相关模型,将在一定程度上为脑动脉血管瘤的临床诊断给出理论指导.
鉴于此,本文构造了分数阶Willis环脑迟发性动脉瘤时滞系统(fractional Willis aneurysm system with time-delay,FWASTD)并对其进行了数值仿真和理论分析:通过与非时滞分数阶Willis环脑动脉血管瘤系统(fractional Willis aneurysm system,FWAS)做对比,验证了其时滞有效性;用传统动力学方法验证系统混沌,探究了时滞给系统带来的丰富动力学行为;利用分数阶时滞稳定性原理实现了FWASTD的混沌控制和自同步混沌控制.本文为脑动脉瘤系统研究和临床诊断提供了相应的理论基础和相关参考.
2 理论知识
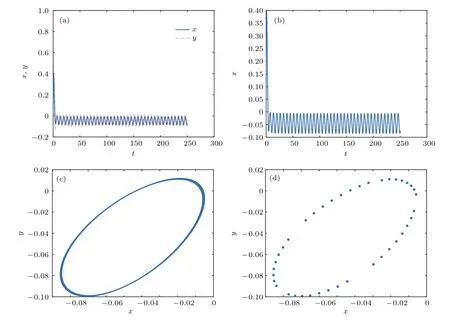
定义1[24]设α是一个正实数,令n−1 6 α 定理1[25]对于带初值的时滞系统 定理2[26]对于分数阶时滞非线性系统,Dαx(t)=f(x(t),x(t−τ)),当分数阶微分阶次0< α<1,f(x(t),x(t−τ))满足Lipschiz条件时,若存在正定矩阵P和半正定矩阵Q,对于任意的状态变量分数阶时滞非线性系统仍然满足 则分数阶时滞非线性系统是Lyapunov稳定的. 从文献[17]可知,FWAS如下: 其中,x和y分别为血流变化率和变化率的加速度;F和µ作为重要的生理参量,分别代表脉冲压和血流阻力;ω,α,β,γ是涉及到心率和血管的生理参量指数,在病理上与动脉瘤状况息息相关[14];q1和q2作为分数阶次可以精细刻画脑动脉瘤系统. 由于临床中血流速度呈现上下波动、不断改变的状态,说明血流加速度存在于血流运动变化中并起着推动血流速度改变的重要作用.一旦血流有显著变化,最开始的病变一定是从血流加速度开始,故引言中提到的尖峰延迟的根源应在血流加速度上,而表现在血流速度上.取时滞因子为τ,将其加入到血流加速度中,构造时滞系统FWASTD如下: 本节用FWAS(系统(1))与FWASTD(系统(2))做对比来说明FWASTD的时滞有效性.根据参考文献[17],取FWAS在混沌状态下的系数,即:α=0.9,β=3,γ=2,F=0.1,µ=0.1,ω=1,q1=1,q2=0.95,对于时滞τ,尝试性地取为1,设FWAS与FWASTD的血流速度分别为x1和x2,利用Matlab 2015b进行仿真,用修正的Adams-Bashforth-Moulton方法[27,28]分别求解FWAS与FWASTD的血流速度,得到两者血流速度的时间序列图如图1所示. 图1 血流速度x1和x2的时间序列图Fig.1.Time course of blood speed x1and x2. 从图1可以看出,x1和x2在区间[700,2000]内几乎重合,但从第2000个时间点左右开始,相比于x1,x2的尖峰值出现延后,延后的时间点大约为800个时间点,从该时间点后,x1和x2仅有部分重合.从引言部分可知,尖峰延后意味着动脉瘤有延迟性破裂的可能.由此可见,FWASTD可以描述不明原因引起的迟发性动脉瘤破裂,也证明了FWASTD的时滞有效性. 3.3.1 FWASTD的分数阶次取值 FWASTD的分数阶次是整数阶次的推广.分数阶算子本身具有记忆性而优于整数阶算子,符合刻画系统生理病情的需要.为了观察分数阶次取值对于系统状态的影响,以期得到最佳刻画混沌状态的取值,现分别取两组组合,第一组组合中固定q1取值分别为0.8,0.975和1,得到关于q2的分岔图和最大Lyapunov指数图;第二组组合中固定q2取值分别为0.75,0.95和1.15,得到关于q1的分岔图和最大Lyapunov指数图.具体结果如图2所示,其中,图2(a)、图2(c)、图2(e)对应第一组组合,图2(b)、图2(d)、图2(f)对应第二组组合,其他参数参照3.2节进行取值. 从图2整体来看,在q1和q2的所有组合里,时滞系统FWASTD均通过倍周期分岔道路通往混沌,分岔图形基本一致,只是取值范围不同,故可从图2得出描述混沌的最佳取值区间,从而解决分数阶次取值问题.图2(c)和图2(d)取值区间类似,其最大值均逼近1,在分岔图中刚好互为固定参数,本文选其组合(q1=0.975,q2=0.95)为下文所用. 3.3.2 FWASTD的时滞取值 为了研究时滞对于系统(2)的影响,给出关于时滞的分岔图,目的是研究时滞可能的取值范围等问题,为后续研究做铺垫.取α=0.9,β=3,γ=2,F=0.1,µ=0.1,ω=1,q1=0.975,q2=0.95,变动时滞参数τ,可以得到hτ(h=0.05为步长)的分岔图,如图3所示. 从图3(a)可知,随着时滞的增加,FWASTD系统(2)从混沌到稳定.为了更细致地研究时滞的区间段,图3(a)里混沌部分被放大得到图3(b),从图3(b)可以看出,混沌主要集中在hτ=0.05和hτ=0.1这两个点上,其他地方并未出现散点,这说明FWASTD仿真的时滞点是离散点,由此可以确定混沌状态下的时滞τ的具体数值分别为τ=1和τ=2,即这两个值是产生系统混沌的关键.之后进行的关于FWASTD仿真的取值点将从这两个点中选取. 3.3.3 FWASTD的仿真 FWASTD作为整数阶WAS的推广,亦能刻画迟发性脑动脉瘤系统的混沌状态,下面针对FWASTD(系统(2))进行仿真验证.取τ=2,α=0.9,β=3,γ=2,F=0.1,µ=0.1,ω=1,q1=0.975,q2=0.95作为参数,可以把FWASTD(系统 (2))写为 图4为系统(3)在时滞状态的时间序列图、相图和Poincaré截面. 图2 系统在给定初值下,q1=(a)0.8,(c)0.975,(e)1时q2的分岔图和最大Lyapunov指数图以及q2=(b)0.75,(d)0.95,(f)1.15时q1的分岔图和最大Lyapunov指数图Fig.2.With a given initial value,bifurcation and largest Lyapunov exponent(LLE)diagram of system versus q2 when q1=(a)0.8,(c)0.975,(e)1;bifurcation and largest Lyapunov exponent diagram of system versus q1when q2=(b)0.75,(d)0.95,(f)1.15. 图3 时滞影响下系统的分岔图 (a)hτ∈[0,3];(b)hτ∈[0.03,0.12]Fig.3.Bifurcation diagram of the system with time-delay:(a)hτ∈[0,3];(b)hτ∈[0.03,0.12]. 从图4(a)和图4(b)可以看出,血流速度紊乱,频频出现尖峰,说明系统呈现出混沌状态;从图4(c)可以看出,其轨迹无规律;再结合图4(d)中系统(3)的Poincaré截面里具有层次结构且成片密集的点,亦证明了系统(3)处于混沌状态,说明阶次为分数的FWASTD也可刻画系统的混沌状态. 图4 系统在给定初值下,(a)x-t,y-t的时间历程图,(b)x-t的时间历程图,(c)相图,(d)Poincaré截面Fig.4.The system with a given initial value:(a)Time course of x-t,y-t;(b)time course of x-t;(c)phase diagram;(d)Poincaré section. 在系统(2)中分别把脉冲压F和血流阻力系数µ作为变量,其他参数参照系统(3)保留不变,得到关于脉冲压和血流阻力系数的分岔图和最大Lyapunov指数图,如图5所示. 多数文献[14,16,17]把研究的重点放在生理参量脉冲压F上,控制也是从脉冲压这一生理参量入手,但从图5(a)分岔图结合最大Lyapunov指数可以看出,其最大Lyapunov指数一直处于0以上,系统持续处于混沌状态. 图5 (a)系统随脉冲压F变化的分岔图和最大Lyapunov指数图;(b)系统随血流阻力系数µ变化的分岔图和最大Lyapunov指数图Fig.5.(a)Bifurcation and largest Lyapunov exponent diagram of versus pulse pressure F;(b)bifurcation and largest Lyapunov exponent diagram of versus coefficient of blood f l ow dampingµ. 从图5(b)分岔图可以看出,随着血流阻力µ的增大,系统从开始处于混沌状态逐渐变为分岔,直至稳定.结合µ的最大Lyapunov指数图可证实系统会随着血流阻力的增加而稳定,临床上亦有促进血栓形成来辅助治疗的记载[14],以上种种均说明时滞状态下研究血流阻力系数对于临床诊断具有重大意义. 由于FWASTD的混沌状态表现为迟发性脑动脉瘤破裂,第一要义是避免动脉瘤破裂,控制混沌.故本节将根据分数阶时滞系统稳定性定理对FWASTD进行控制并实现同步控制. 下面将证明具有初值条件的FWASTD存在惟一解且满足Lipschitz条件. 定理3 构造具有初值条件的系统如下: 其中, 则含有初值条件的FWASTD(4)存在惟一解. 证 明 取|·|和∥·∥分 别 为 向量范 数 和 矩阵范数. 令F2(X(t)).对于∀δ>0,区间连续并有界.取有 则因区间[X0−δ,X0+δ]连续有界,α,β,γ是有范围的生理参数,因此L1是个常数,于是对于有 故G(t,X(t))除t外所有变元满足Lipschitz条件,根据已知条件G(t,X(t))在给定初值的邻域内连续,所以G(t,X(t))满足定理1,即具有初值条件的FWASTD存在惟一解.定理3证毕. 取和系统(3)相同的参数,得到有初值条件的FWASTD如下: 从图4的仿真结果可以看出相图轨线无规律,Poincaré截面具有一定层次结构和形状,因此具有初值条件的系统(5)不处于稳定状态. 对系统(5)设计线性控制器: 定理4 当k1>0.5,0 6 k26 0.9,k3>1.95时,系统(5)稳定. 根据定理2,系统(6)是Lyapunov稳定的. 取k1=0.5,k2=0.9,k3=1.95,系统(6)仿真结果如图6所示. 从图6(a)和图6(b)可以看出,x,y随着时间增长在[−0.2,0.1]波动,仿真结果证明,该控制器可以把FWASTD控制在一个比较稳定的范围之内,虽然有周期性波动,但是波动振幅小(上下不超过0.1),满足混沌控制需要.图6(c)和图6(d)也说明了具有线性控制器的FWASTD处于比较稳定的状态,体现在实际中表现为血管中血流速度和加速度基本保持稳定,病情处于可控状态.近年来,在血管内使用血流导向装置成为治疗脑动脉瘤的一种主流办法.血流导向装置可以通过改变血流速度和加速度等血流动力学因子来改善动脉瘤内部的血流情况从而达到治疗疾病的目的,但现有的血流导向装置在设计和材料使用上仍有缺陷[29],本文为其提供了相关的设计参考. 下面考虑FWASTD同步控制,把FWAS作为驱动系统: 图6 (a)x-t曲线,y-t曲线;(b)时间历程;(c)相图;(d)Poincaré截面Fig.6.(a)Curves of x-t and y-t;(b)time course;(c)phase diagram;(d)Poincaré section. 把带控制器的FWASTD作为响应系统: 误差系统为 数值仿真验证时,取τ=2,α=0.9,β=3,γ=2,F=0.1,ω=1,q1=0.975,q2=0.95,µ=0.1,k1=−0.5,k2=−2.1,k3=1.1,t表示时间,误差系统仿真结果如图7所示. 图7 (a)e1随时间的变化;(b)e2随时间的变化Fig.7.(a)Curve of e1with time change;(b)curve of e2with time change. 从图7(a)和图7(b)可以看出,其误差逐渐趋于0,由此可见,FWASTD和FWAS可以实现同步.实际治疗中,由于许多生理参数无法确定等原因,时滞系统FWASTD无法得到像4.2节那样精准的混沌控制,然而从自同步控制过程可以看出,其控制参数主要依赖于血流阻力参数,控制变量少且易得,而FWAS可以通过脉冲药物等进行控制,操作简单可控,更符合实际. 鉴于治疗过程中有可能会因治疗方式等不明原因引起迟发性动脉瘤破裂的实际情况,本文提出FWASTD,经过与非时滞系统的对比,说明了时滞的有效性,通过理论证明和数值仿真,论证了其丰富的混沌性质并分析了时滞对系统造成的影响.其中尤为重要的是,研究表明FWASTD系统在一定条件下随血流阻力的增加而稳定,与临床上的促进血栓形成来辅助治疗[10]形成较为明确的对应关系,说明血流阻力系数研究对于临床诊断具有一定意义. 同时,利用分数阶时滞系统的稳定性理论设计了合适的线性控制器以对FWASTD进行有效控制及同步控制.本文提出的FWASTD对脑动脉瘤里的时滞研究提供了理论基础,在一定程度上为脑动脉血管瘤的临床诊断和治疗提出了理论指导.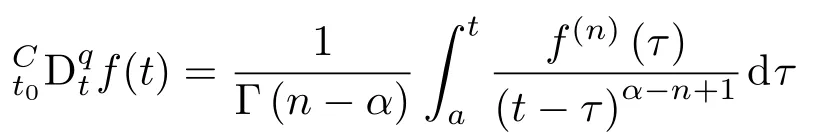



3 FWASTD及其性质
3.1 建立FWASTD


3.2 FWASTD的有效性

3.3 FWASTD的取值和仿真
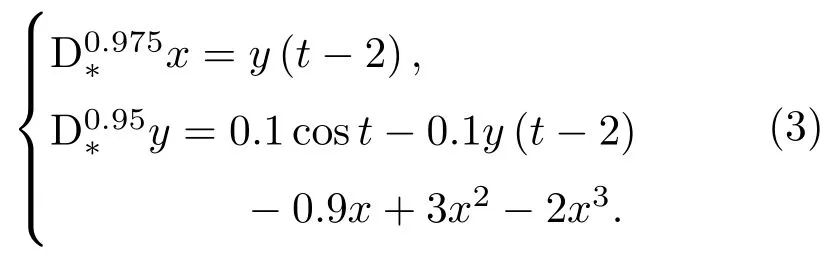


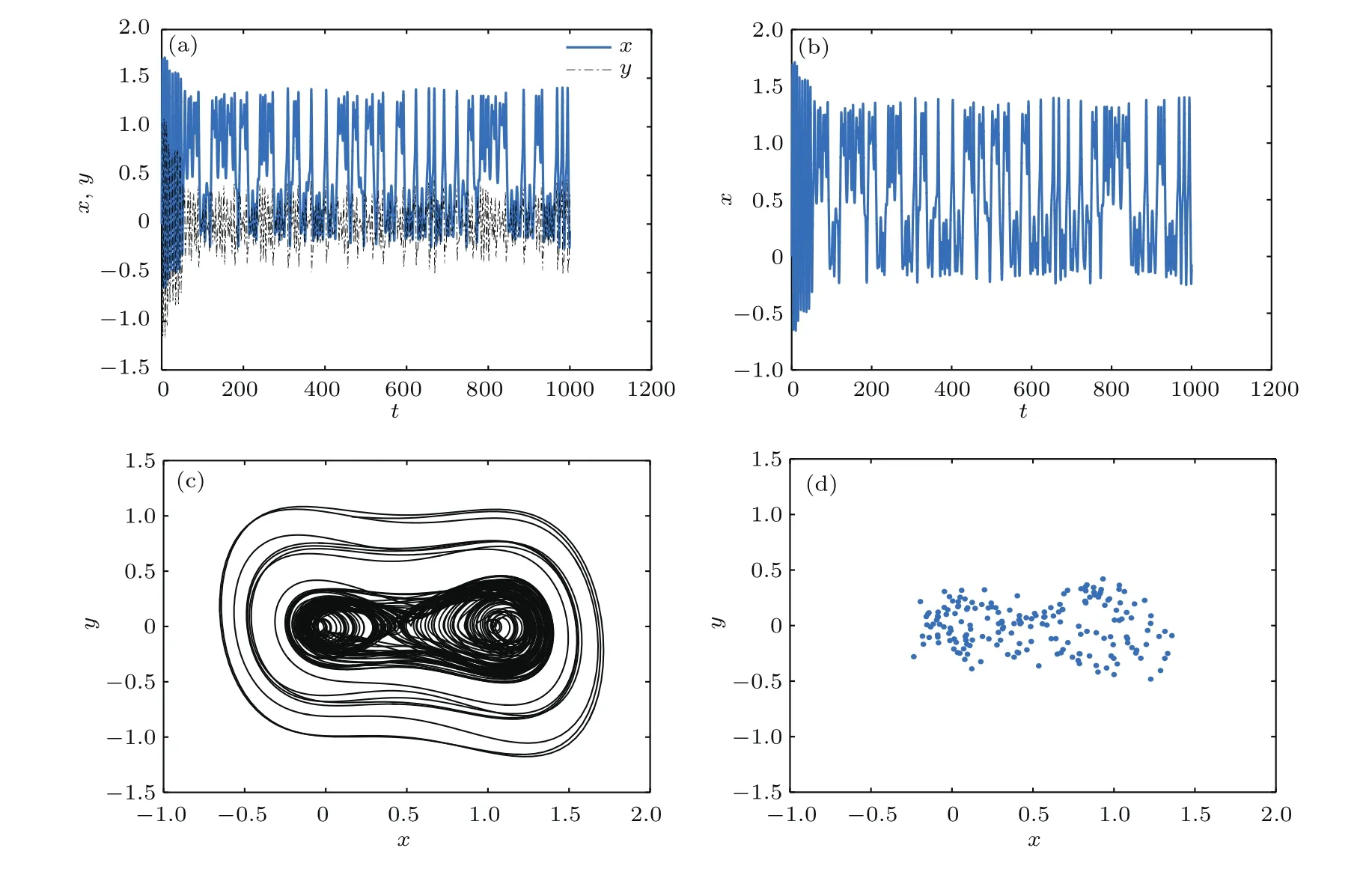
3.4 FWASTD中脉冲压和血流阻力系数对系统的影响

4 FWASTD的控制
4.1 时滞系统解的惟一性分析


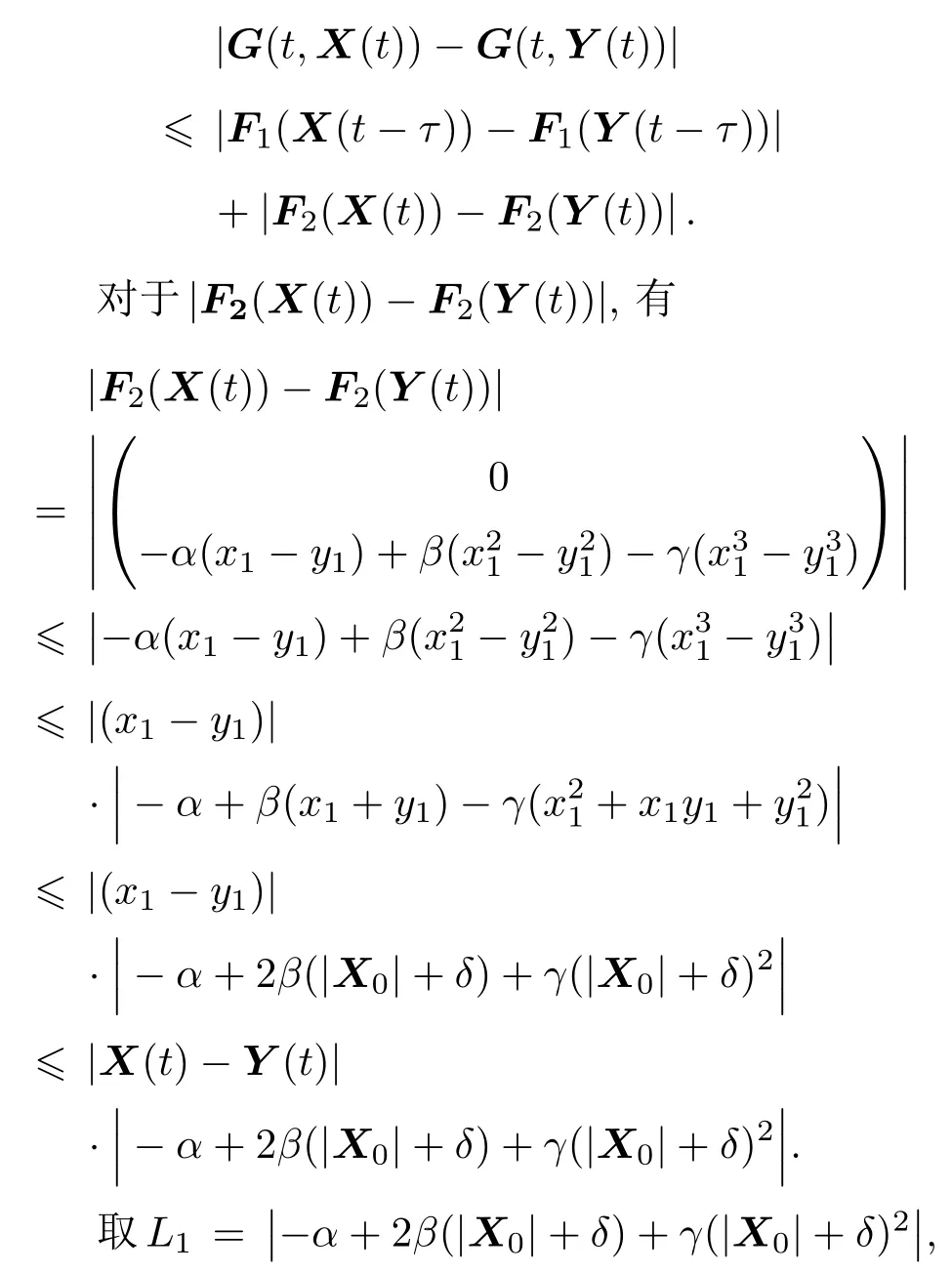
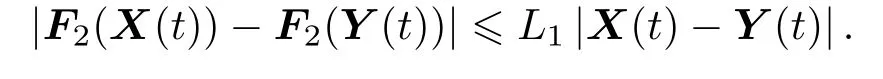
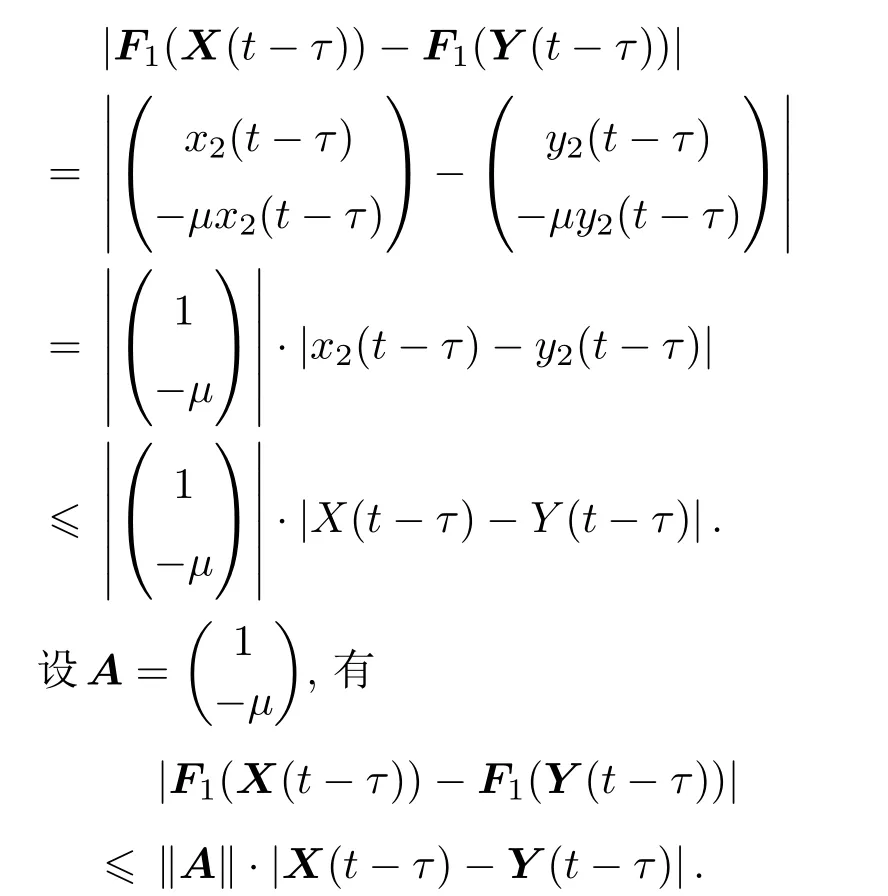
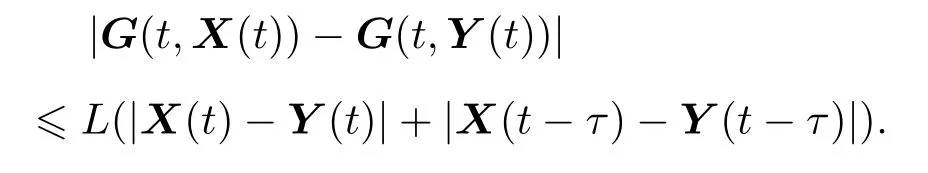
4.2 FWASTD的混沌控制



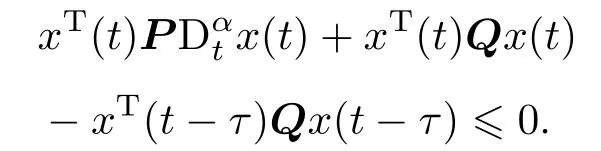
4.3 FWASTD的同步控制

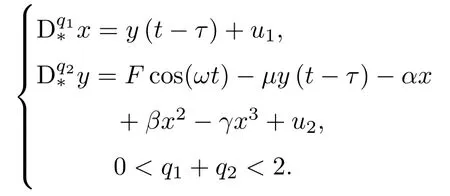
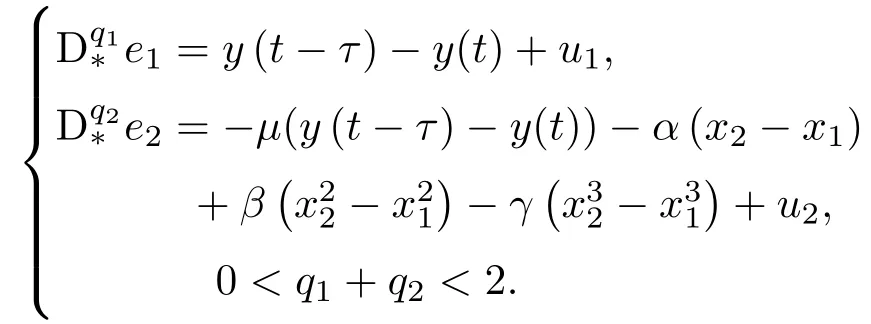



5 结 论
