运动目标激光微多普勒效应平动补偿和微动参数估计∗

郭力仁 胡以华 董骁 李敏乐

(国防科技大学电子对抗学院,脉冲功率激光技术国家重点实验室,合肥 230037)(2017年12月28日收到;2018年4月26日收到修改稿)

1 引 言

运动目标都会存在由于发动机振动、旋翼转动等引起的相对于整体平动而言的微运动.这些微动会对探测信号造成多普勒效应外的附加频率调制,产生微多普勒效应[1].不同目标的微动特征具有惟一性,开辟了探测和识别的新途径.现有的微多普勒研究主要用于目标分类,但通过对目标运动和微动参数的精确估计,再结合充足的目标先验信息,还可开创性地实现对同类目标的精细识别.实际的遥感目标振动幅度在微米量级,如汽车、飞机发动机运转引起的表面振动等.微波探测对此类微多普勒效应并不敏感,但采用波长更短的激光探测手段,可以得到更为显著的微多普勒频移[2],具有更高的灵敏度和分辨率,有利于提高参数估计及目标识别的准确性.

目标运动产生的多普勒效应一般可用多项式相位信号(PPS)进行建模,而目标微动广泛采用正弦运动模拟,其回波是典型的正弦调频(SFM)信号[3,4].两者在回波中形成PPS-SFM混合信号,这在目标探测的工程应用中普遍存在[5].但是,目前多数对目标微多普勒特征的研究只考虑回波为SFM模型[6],忽略了目标整体运动的影响.对于混合信号,传统的适用于纯SFM信号或PPS的估计算法都不再适用.而现有的针对混合信号参数估计的研究又存在估计误差大、计算过程复杂的不足.一般而言,直接估计平动微动混合信号参数难以实现,实际操作中往往先将两项分离再分别进行估计.分离方法可大致分为两类[7],即基于时频分布类和基于信号模型变换类.前者对信号进行时频分析,提取信号的瞬时频率特征[8,9],利用多项式拟合补偿平动分量,再对剩余微动分量进行参数估计[10,11].该类方法有利于直观地观测信号调频特征及各步处理效果,但对信噪比要求较高,且受限于时频分布分辨率、峰值提取准确度、多项式拟合精度等多重影响,存在多层误差传递,估计精度和时效性较差,甚至会出现运动阶数的错误估计.后者则根据两类信号的不同特性,利用高阶模糊函数[6]和延时共轭相乘法[12,13]逐阶消去信号中多项式相位,只保留SFM再进行参数估计,但都需要目标运动阶数这一先验信息,且运算过程复杂.此外还有通过粒子滤波(PF)[14]、广义周期[15]法从信号层面对混合信号进行估计,但只考虑了固定载频的情况,相当于匀速运动产生的一阶PPS,模型比较简单,不适合目标实际运动情况.

在激光探测的微多普勒信号参数估计中,由于探测波长短、采样率高,对SFM部分参数估计时将产生较微波探测非线性程度更高的代价函数[16],密集的局部峰值极易使传统的迭代类方法、统计类方法不收敛或错误收敛[17],同时计算量也会随参数数量的增加而呈指数上升.现有的SFM变换[18]和循环自相关[19]等参数估计方法都只针对两参数的简化模型,不适合处理实际的多参数信号.对于以上的混合信号分离和微动参数估计问题,本文提出基于分数阶傅里叶变换(FrFT)的平动补偿方法,通过设计FrFT参数域的带宽搜索方法,可以从混合信号中精确估计平动参数,实现平动和微动的分离.对补偿后的信号,通过改进的静态参数PF方法估计其中的微动参数,所提方法不受噪声类型限制,可同时估计多个参数,避免误差传递的影响,而且估计参数数量的增加并不会过多地增加算法的计算量.利用累积残差定义新的权重函数,并用马尔可夫-蒙特卡罗(MCMC)保持粒子多样性,保证了静态参数模型下PF的快速有效收敛.通过对算法估计性能进行仿真和实验分析,本文方法可实现对平动和微动混合信号参数的准确估计.

2 基于FrFT的平动参数估计

2.1 运动目标微多普勒信号模型

利用点散射模型对微多普勒效应进行建模[1],经过后续化简和整合,各类微动的点散射模型都具有SFM信号的基本形式.若考虑目标微动特征平稳,信号处理中一般只需要一到两个周期的信号长度就可以实现对微动参数的估计.实际目标的微动

频率多在百赫兹量级甚至更高,所以要求处理的信号时长很短.对于平动,人们常采用PPS进行模拟,在较短的时间内,平动相对于微动是缓变量,用匀加速运动的模型可完全满足对平动的模拟,这时信号平动引起的多普勒效应表现为线性调频(LFM)信号的形式.所以运动目标微多普勒效应回波基带信号可表示为

式中,ν表示目标运动初速,a表示加速度,λ表示激光波长,Dv表示目标微动幅度,fv表示目标微动频率,ρ0为微动初始相位,f0和µ0分别对应目标的速度和加速度项,fmD表示微多普勒频率项,为简便起见,模型中考虑散射点振动方位角和俯仰角及目标相对于雷达的方位角和俯仰角为.θ0为信号初始相位,noi(t)为信号噪声.

目前对微多普勒效应的研究大多只针对微动引起的SFM模型展开,而不考虑平动对微动特征的影响.事实上,未补偿平动或只用测速数据粗略补偿的信号都是一个LFM-SFM的混合形式,平动分量的存在会破坏微多普勒特征的周期性,导致现有微动参数估计方法的失效.而且平动还会使频谱展宽,对采样率和探测器带宽都提出了更高的要求,对于同样时长的信号,需要处理的数据点数会极大地增加,导致运算量剧增,所以有必要先对平动参数进行精确估计和补偿.

2.2 平动参数估计原理

FrFT可看作是在一组正交的LFM信号基上展开信号[20].所以,一个确定的LFM信号可以在FrFT的某一阶次上得到最好的能量聚集效果[21].定义信号s(t)的p阶FrFT为

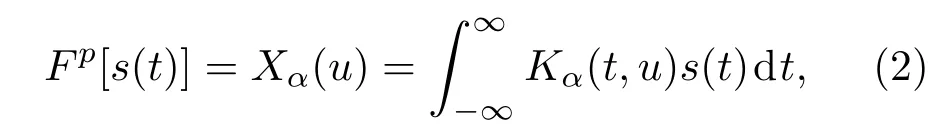
式中阶次p可以为任意实数,角度α=pπ/2;Kα(t,u)为FrFT的变换核,可表示为

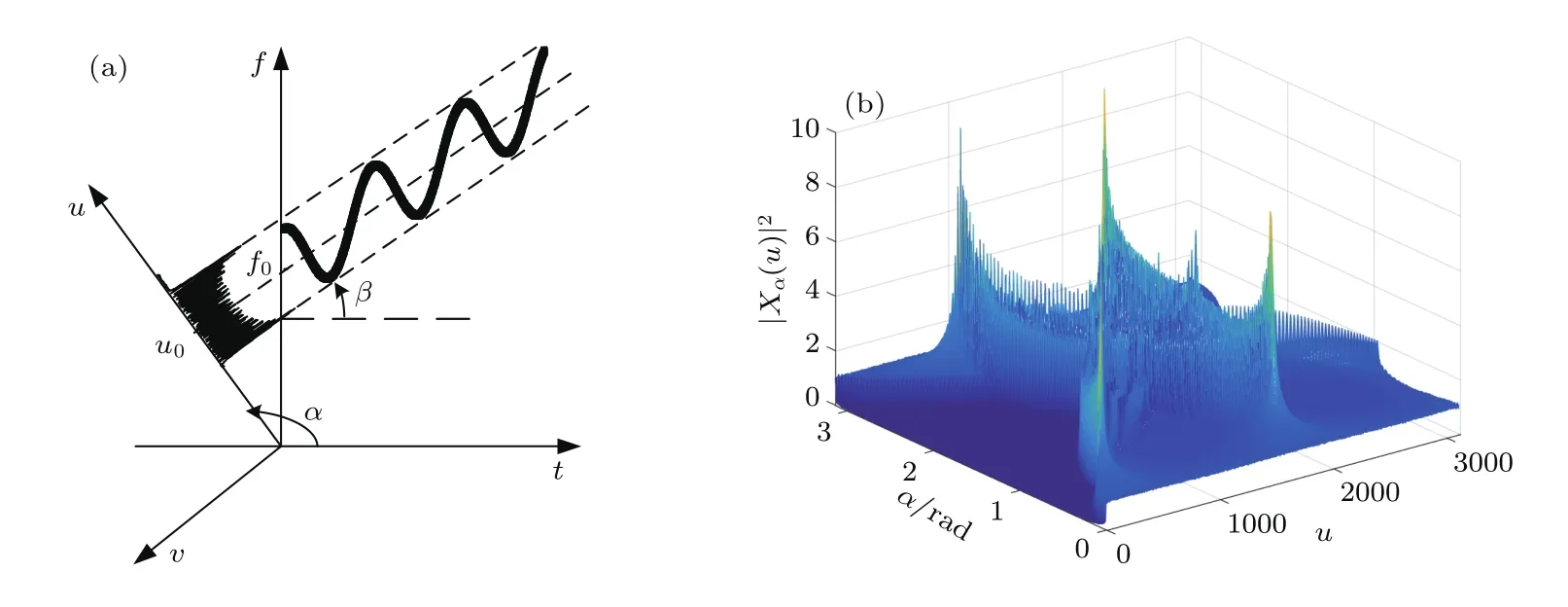
图1 LFM-SFM信号FrFT示意图 (a)能量聚集原理;(b)(α,u)域分布Fig.1.FrFT on LFM-SFM signal:(a)Energy accumulation principle;(b)FrFT distribution in parameter f i eld.

本文研究的运动目标微多普勒信号表现为LFM-SFM混合的信号形式,经过FrFT的结果如图1所示.

从图1可以看出,对于混合信号进行FrFT在对应的α下不是向单纯的LFM信号一样聚集到一点,而是在u域有最窄的带宽,从图1(b)可以看到继续采用传统的最大值搜索法来确定LFM项参数显然已经不再合适.这里提出双向阈值搜索法来精确计算各u域的带宽.用M×N维矩阵F表示FrFT参数域分布,其中M为对α离散化扫描的次数,与步进长度成反比;N为信号长度.

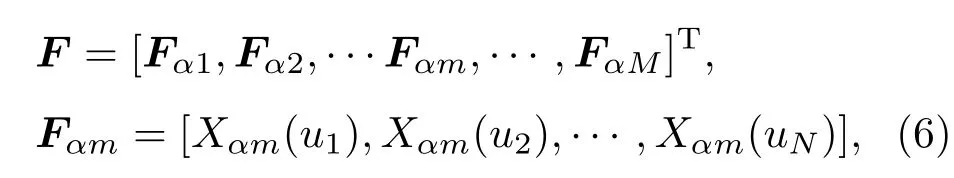
式中,Fαm表示FrFT在第m行的分布向量,对每行的Fαm取均值作为该行的阈值th(αm).带宽搜索原理如图2.

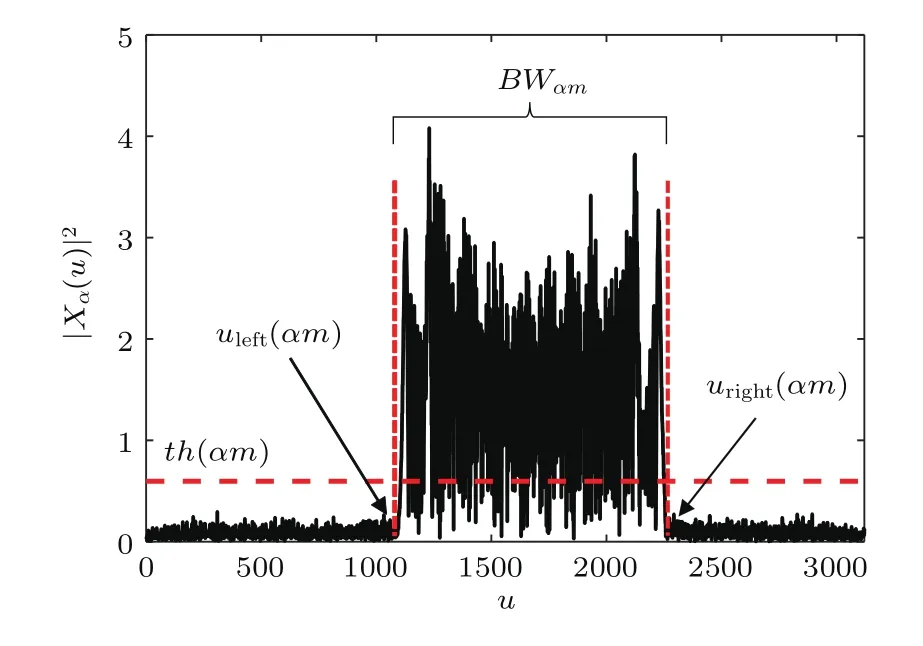
图2 双向阈值搜索法u域确定带宽Fig.2. Bandwidth determination by bidirectional threshold searching method.

图2中首先对Fαm行进行正向搜索,将第一次出现大于阈值的u作为带宽的左边界,有然后再对进行反向搜索,确定带宽的右边界其中表示对括号中的向量进行左右反转操作. 此时第m行的u域带宽等于所以通过搜索矩阵F各行最窄的带宽,再代入(5)式就可以确定平动参数,注意此时这里应注意阈值的选择应与信号信噪比关联,当信噪比较低(<10 dB)时,为避免噪声对带宽边界搜索的干扰,阈值可取为均值的两倍.

得到平动参数后重构相应的多普勒分量sD(t),并将其从混合信号中去除,实现平动补偿,此时剩余信号中只包含微多普勒效应.

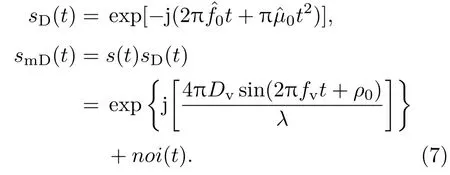
3 基于静态参数PF的微动参数估计

3.1 静态参数PF模型

基于PF的参数估计方法不受信号模型的限制,可实现多参数同时估计,避免误差传递,保证每个参数的估计精度.SFM参数估计在PF中属于静态参数估计问题,以(7)式中的补偿结果smD(t)作为系统的观测方程,微动参数作为状态方程,有

式中Yt为t时刻观测值,Xt为t时刻粒子状态,t时刻第i个粒子可写为对于静止参数模型,粒子多样性不会增加,只能在初始化形成的粒子组中寻找最优解,无法保证正确收敛,所以需要加入抖动vt,来维持粒子的多样性.此时,vt相当于粒子状态的更新量,当vt过大时,粒子更新幅度也较大,不利于参数的精细搜索,容易出现无效的迭代计算;当vt太小时,粒子每次的更新幅度也较小,需要大量迭代才能收敛,效率较低.所以vt决定了整个算法的效率.本文采用MCMC[22]算法更新粒子状态,算法的建议分布方差就等效于模型中添加的抖动vt,效果相当于在随机更新的基础上加入了方向的选择,使粒子始终向真值方向更新,有效减少了收敛所需的迭代次数.

3.2 多维参数权值计算

根据序贯重要性采样方法[23],重要性密度函数取此时各粒子权重可化简为

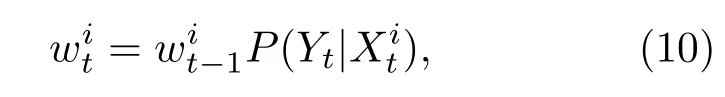
3.3 粒子状态更新

对于多参数情况,同时产生所有参数的候选状态时,由于各参数粒子间随机匹配,难以得到高权值的粒子组合,这会导致极低的接收概率,粒子可能长时间得不到更新,不仅对改善粒子多样性没有任何帮助,还会降低运算效率.对此,本文提出自适应方差Gibbs算法来具体实现,虽然增加了单次抽样的计算量,但接收概率更高,整体上是加快了收敛,具有更高的效率.

自适应方差是指根据实时的估计误差来调整算法建议分布的方差,在初始时,粒子往往与真值差距较大,这时选用较大的方差来提高候选状态在整个支撑域上的搜索范围,以便于快速更新到真值附近,相当于粗搜索;当几次迭代搜索之后,残差变小,则减小方差,使其在真值附近精细搜索,提高样本接受概率和参数估计精度.自适应方差法可表示为

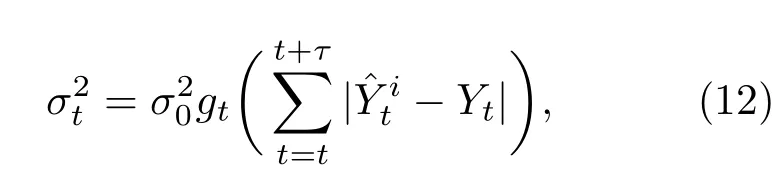
3.4 静态参数PF参数估计流程

PF前首先要解决多维参数初始化的问题.对于未知参数值,一般在取值范围内随机产生初始值,这需要大量的粒子数目来提高产生优质初始粒子的概率,但过多的粒子会导致后续繁重的计算量.对此提出变粒子数目的PF方法:首先设置较大的初始粒子数目,计算各粒子组的权重,只保留权重较高的少数粒子作为之后迭代的初值.该方法可提高初始值的质量,并避免在低权重的粒子上进行无谓的计算,优化了算法效率.应当说明的是,算法只在初始化后进行一次减少粒子数的操作.

PF的终止条件可通过设置累积误差阈值Rstop来进行判断.本文利用静态参数PF进行目标微动参数估计的流程图如图3.

具体的算法步骤可以总结为:

1)确定参数范围,设定粒子数为Np,初始化粒子迭代次数t=0;

5)根据(12)式确定建议分布方差,采用MCMC算法更新粒子状态,保持多样性;

图3 静态参数PF算法流程图Fig.3.Flow chart of static parameter PF algorithm.

4 仿真分析与实验验证

4.1 仿真信号参数估计

4.1.1 平动补偿

设目标为4缸发动机的汽车,发动机转速为3000 min,每缸点火一次产生一次振动,根据发动机工作原理,对应的振动频率为fv=3000×2/60=100 Hz,目标表面振动幅度Dv为5µm,振动对信号调制的初始相位ρ0为π/6 rad,激光波长为1.55µm,信噪比为20 dB.设目标平动引起的多普勒参数为f0=104Hz(认为是初步的平动补偿后的残余分量),µ0=4×106Hz,对应的加速度为3 m/s2,仿真信号的时频分布如图4所示.

图4中LFM-SFM信号的瞬时频率特征为两者的融合,两者相互影响破坏了两种信号原有的时频特征,传统的针对单纯的SFM或LFM信号特征的提取方法已不再使用.根据2.2节所提方法对平动参数进行估计,得到FrFT参数域分布及带宽搜索结果如图5所示.

图5(a)中颜色较亮的区域对应能量聚集区域,两侧亮暗交界线即对应各旋转角下的u域带宽.当α与信号中LFM对应的瞬时频率曲线垂直时,信号在u域有最好的能量聚集,此时带宽最窄.图5(b)为双向阈值搜索法估计出的带宽随α的变化趋势,与图5(a)中的亮暗交界线包络的变化趋势一致,证明了带宽估计方法的正确性.确定带宽最小时的α值,代入(5)式计算LFM参数,并和目前典型的基于时频特征多项式拟合的平动参数估计方法进行对比.

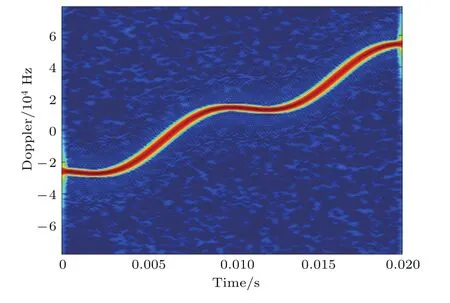
图4 LFM-SFM混合信号时频分布Fig.4.Time-Frequency distribution of LFM-SFM signal.

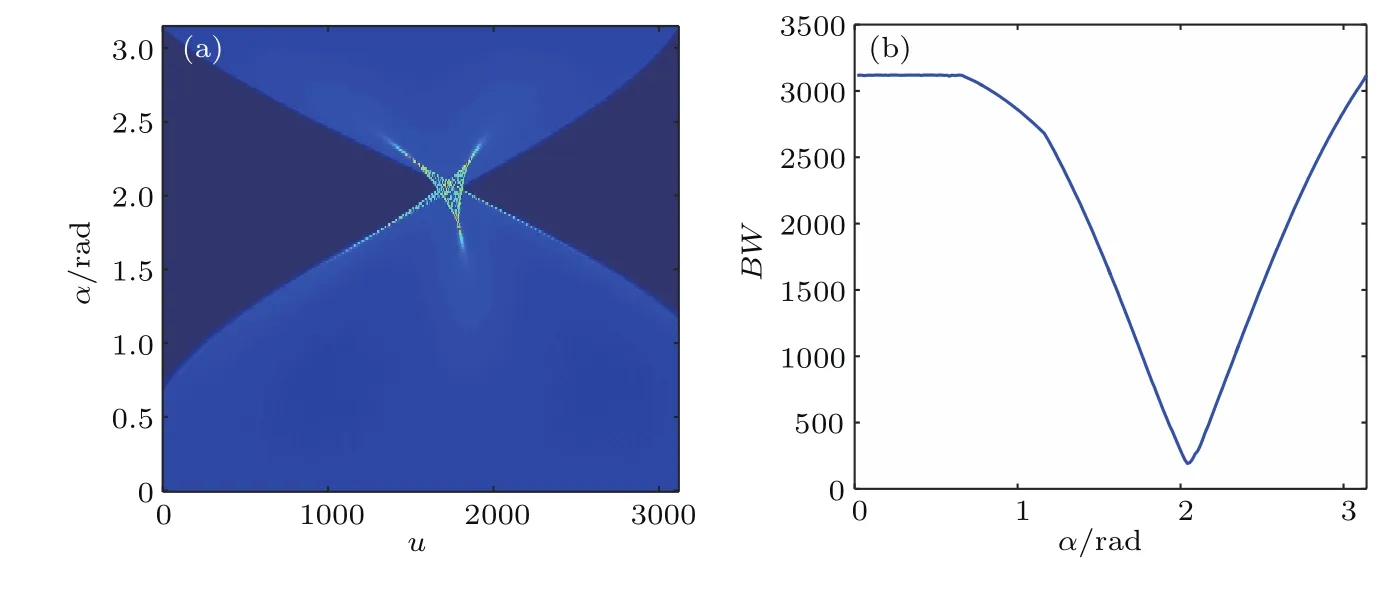
图5 FrFT对混合信号处理结果 (a)FrFT在(α,u)域投影;(b)u域带宽随α的变化Fig.5.FrFT results of LFM-SFM signal:(a)Projection on(α,u)domain;(b)bandwidth changes with α.

表1 平动参数估计结果对比Table 1.Comparison of translational parameter estimation results.

表1中处理的信号时长为两个微动周期,可以看出拟合法得到的参数估计精度受微动时频特征初始相位影响极大,这可通过图1(a)进行解释,不同的初相导致瞬时频率曲线的起始位置和中心频率之间距离不同,而这个距离会直接影响拟合的结果.当初相为π/2时,起始点恰和中心频率重合,不存在拟合误差,所以此时平动参数估计精度最高,而在其他相位下,估计结果会存在不同程度的误差,且远高于本文参数化方法的估计结果.相比之下,本文采用了基于投影原理的参数估计方法,不受信号初相的影响,具有稳定的估计精度.

对目标平动的补偿效果会直接影响到后续微动参数的估计精度.这里用平动补偿后信号与实际SFM信号的相位波形相似度作为标准对LFM参数的估计精度提出要求.定义波形相似度为图6为真实SFM相位和经过平动补偿后的信号相位在γ=0.9999时的波形对比.图7为波形相似度随LFM参数估计相对误差的变化情况.

从图6可以看出,γ=0.9999时两波形基本重合,此时可以认为后续的微动参数估计不受影响.图7中γ随参数相对误差的增加逐渐降低,通过对γ的限制可以确定可容忍的LFM参数估计精度.从图7可以看到,在时,要求REf0<10%就可保证γ>0.9999,而本文方法求出的REf0=0.45%,完全满足要求,而拟合法只有在微动初相为π/2时才能满足要求.当然,通过增加处理信号的长度可以减小拟合法的误差,结果列于表2.

表2中,T=1/fv表示一个微动周期的信号长度,Tope表示算法运行时间.可以看出,随着信号长度的增加,估计误差不断降低,这是因为信号越长,端点的误差对拟合的影响越小.但过长的信号也增加了时频分析算法的运算时间.而文中提出的FrFT方法只需两个周期长的信号就可实现更低误差的参数估计,而且运算时间远低于相同条件下的时频分析拟合方法.

图6 γ=0.9999时的相位波形对比Fig.6.Waveform comparison at γ=0.9999.

图7 γ随LFM参数相对估计误差的变化Fig.7.Relation between γ and relative error.

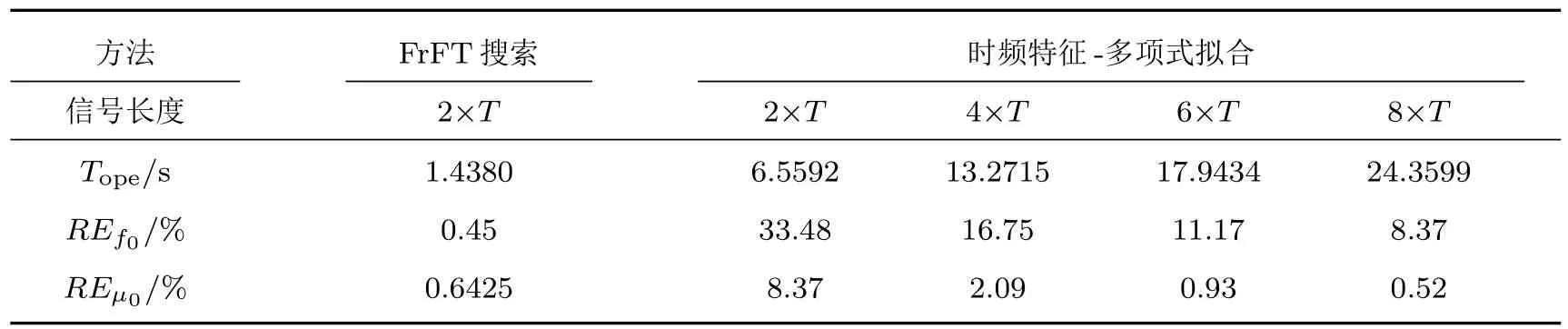
表2 不同信号长度估计结果对比Table 2.Comparison of estimation results under dif f erent signal lengths.

4.1.2 微动参数估计

令初始时粒子数Np为400,计算各粒子组的权重,只保留权重较高的400个粒子作为下一次迭代的初值.残差累积长度为200个采样点,将观测估计值的相对误差连续稳定且小于0.001作为迭代结束的条件.

首先分析粒子初始化对算法结果的影响,对于未知参数,根据经验设置初始化范围:[50,150]Hz,Dv∈ [2,10]µm,ρ0∈ [0,π/2]rad.不同初始粒子数下的仿真结果如图8.

从图8(a)可以看出,对于多维参数而言,较少的粒子数不足以产生优质的初始参数组合,所有粒子的累积残差都处在一个较大的水平(>350).当粒子数增多时,在相同的参数取值范围下,多维参数组合的多样性增加,产生接近真实值的概率也随之增加,如图8(b),出现了残差小于200的初始粒子.根据3.4节的变粒子数初始化方法,只取权值高的部分粒子进行PF,并与图8(a)代表的固定粒子数方法进行对比,用估计残差反映估计参数和真实值的近似程度,得到图8(c).图8(b)代表的变粒子数方法只在第一次迭代时处理较多的粒子,计算量较大,之后迭代的计算量与传统方法相同,两算法整体计算量几乎一致,但从对比结果可见前者的估计残差明显低于固定粒子数方法,且不到1次迭代就实现了收敛,而固定粒子数方法则由于初始值质量较差,PF过程中残差一直处于较高水平,不能确保正确的收敛,仿真结果体现了本文初始方法的有效性和必要性.

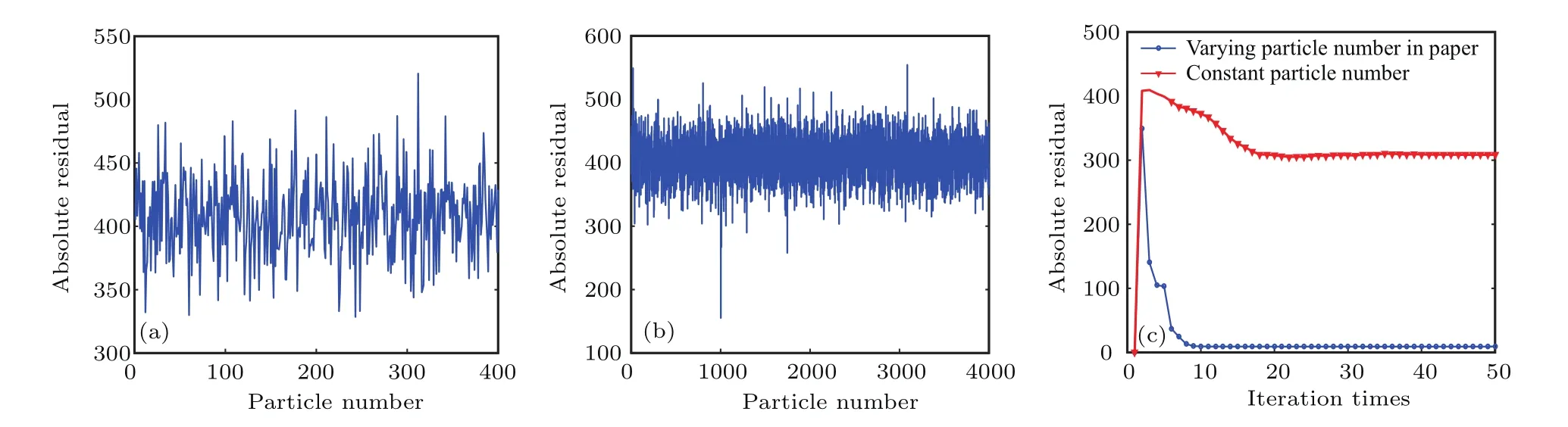
图8 初始化值影响 (a)Np=400;(b)Np=4000;(c)不同初始值的估计结果对比Fig.8.The inf l uence of the initial value:(a)Np=400;(b)Np=4000;(c)etimation results of dif f erent initial values.

考虑到算法的收敛效率与建议分布σ2的取值密切相关,在参数估计前,应先确定方差σ2.根据3.3节对方差的分析,本文对方差和算法效率之间的关系进行了仿真,并与常用Metropolis-Hastings(MH)算法的性能进行了对比.最高迭代次数设为100,对各σ2值进行100次蒙特卡罗仿真取平均.由于不同参数对应方差不同,这里主要对进行自适应部分的方差进行仿真,它对各参数的作用相同,可以概括地反映方差与迭代次数的关系,结果如图9所示.

图9 方差与算法迭代次数的关系Fig.9.Relationship between variance and iteration times.

仿真中用算法稳定所需要的迭代次数反映算法效率,从图9可以看出,相比于文献[14]中采用的MH算法,在同样条件下本文方法实现收敛的迭代次数更少,说明本文方法效率更高.MCMC建议分布方差存在最优选择获得最佳的算法效率,对于本文设置的参数,最优方差在10−12.当方差逐渐大于最优值时,算法仍可收敛,但迭代次数增加,因为大的方差导致粒子候选状态的接受概率降低,但至少在范围上可以覆盖真值;当方差逐渐小于最优值时,算法甚至在100次的迭代中无法实现稳定,这是因为状态更新幅度太小,粒子需要大量迭代才能接近真实值.

从图10可以看出,本文所提算法采用了变粒子数、Gibbs多维更新算法和自适应方差后,只用了不到10次迭代便使估计值收敛至真值,而只采用传统MH算法去实现PF,需要40次左右的迭代才能实现收敛.如果未使用最佳σ2进行估计,算法效率将更低,需要更多次迭代才能实现收敛[14].下面对比两种方法单次迭代运算的时间复杂度.本文方法为其中τ为通过累积残差计算粒子权重时设定的累积时间长度(具体分析见3.1节);p为估计参数个数;第二项表示重采样带来的时间复杂度;第三项表示状态更新的时间复杂度.经典的MH算法一次迭代的时间复杂度为两者差别主要体现在多维粒子状态的更新运算上.记录算法每次迭代的运行时间,其中本文方法为0.0353 s,MH方法为0.0211 s,综合考虑算法收敛所需的迭代次数,前者耗时0.353 s(1次迭代),后者0.844 s(4次迭代),本文方法整体上用时更少,效率更高.从计算复杂度的角度来看,即使待估计参数的数量增加,也并不会过多地增加本文算法的计算量.

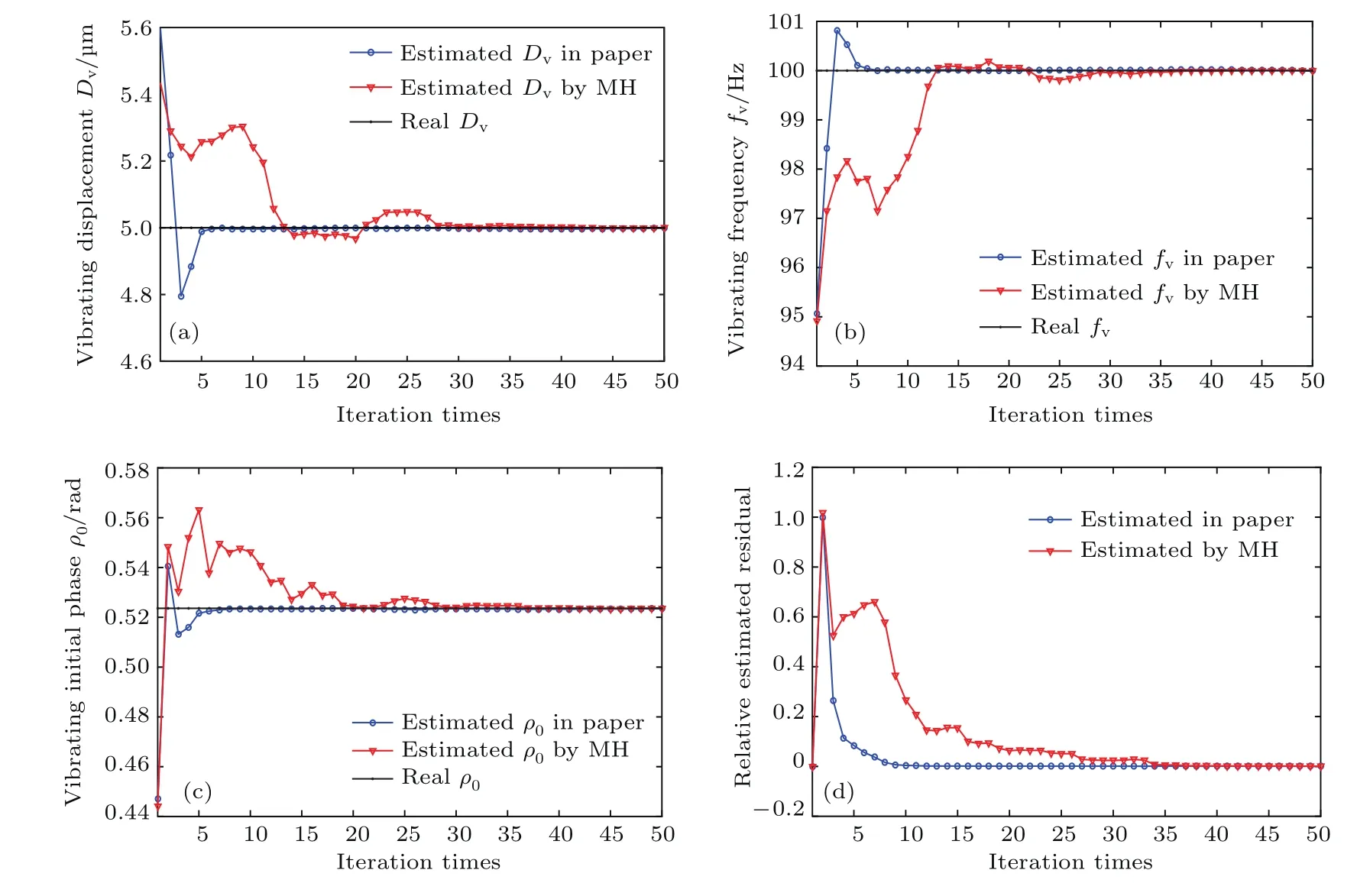
图10 参数估计结果随迭代次数的变化 (a)振动幅度;(b)振动频率;(c)振动初相;(d)相对误差Fig.10.Estimation results changing with the iteration times:(a)Vibration amplitude;(b)vibration frequency;(c)vibration initial phase;(d)relative estimated residual.

4.2 实验数据参数估计

对实验数据进行处理估计目标微动参数来验证算法有效性.实验设置如图11所示.

实验装置为全光纤结构,采用波长1550 nm连续波激光器,输出功率40 mW,线宽小于0.1 kHz.激光器输出光通过保偏光纤分束器,分为90%和10%两路.其中光强强的一路作为信号光,经过口径为20 mm的光纤准直器照射到目标上;光强弱的一路则经过可调衰减器,作为本振光.信号接收采用口径为80 mm的透射式望远镜,将接收信号光和本振光通过2×2保偏光纤耦合器后输入带宽为80 MHz的InGaAs平衡探测器.输出的中频电信号由12 bit的A/D采集卡采集,采样率在10—500 MHz可调.目标为振膜扬声器模拟微动目标,扬声器驱动信号的振动频率设为256 Hz,振幅约60µm,振动初始相位由截取信号的时刻决定.利用本文算法对回波信号微动参数进行估计,结果如图12所示.

图11 实验系统结构图Fig.11.Structure diagram of experiment system.

图12 实验数据参数估计结果 (a)振动幅度;(b)振动频率;(c)振动初相Fig.12.Parameter estimation for experiment data:(a)Vibration amplitude;(b)vibration frequency;(c)vibration initial phase.

图13 时频分布IRT方法参数估计结果 (a)回波信号时频分布;(b)IRT变换结果Fig.13.Parameter estimation results of IRT:(a)Time-frequency distribution;(b)IRT results.

图14 重构信号与实验信号对比 (a)IRT方法;(b)本文方法Fig.14.Comparison of reconstructed signal and experiment signal:(a)IRT;(b)proposed method.

从图12(a)—(c)可以看出,在经过约30次迭代后,本文算法对实验数据微动参数的估计开始收敛,实现了对目标微动参数的估计.与传统的基于时频分布逆Radon变换(IRT)的方法[24]进行对比,验证本文的参数估计效果.

从图13的IRT结果可以看出,基于时频分布的参数估计只能把微动参数的估计定位到一个大致区域,并不精确到具体值,这难以保证估计精度.而且,IRT定位的参数区域大小严重依赖于时频分布的分辨率,会存在严重的误差传递影响.图14为利用估计参数重构的信号和实验测得信号的对比,从图14(a)可以看到,IRT估计的参数重构信号与实验观测信号差别较大,而图14(b)中本文方法得到的两波形基本重合.用两者波形相似度γ和平均绝对误差来对比参数估计的性能,结果列于表3.

从表3中可看出,参数化的PF方法在两个评价标准上都优于基于非参数化时频分析的IRT,体现了所提方法在参数估计精度上的优势(STFT表示短时傅里叶变换).

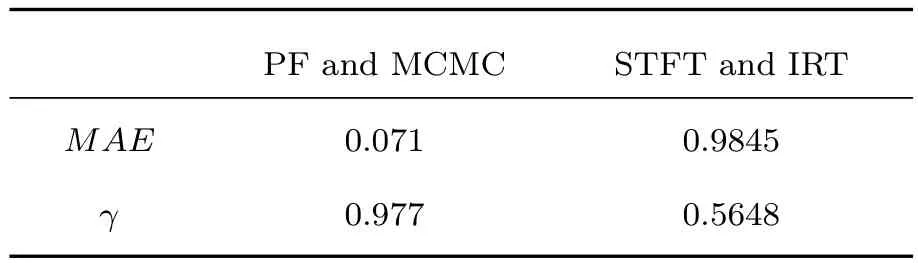
表3 估计性能对比Table 3.Estimation performance comparison.

实验结果验证了算法对微动参数估计的正确性.实际估计的微动频率在257 Hz附近,与设置值256 Hz有差别,这是由于驱动源自身的误差和扬声器自身对信号存在的响应误差,导致了实际振动频率和设定频率有微小差距.

5 结 论

本文以基于微多普勒特征参数的目标识别这一新应用为研究背景,对实际运动目标探测中遇到的平动和微动混合信号模型提出了一种精确的分离和参数估计方法.通过定义平动补偿信号与理想微多普勒信号波形相似度参数,给出了对平动参数估计精度的要求.利用FrFT理论结合参数域最窄带宽搜索,可以实现满足精度要求的平动参数估计,完成对LFM-SFM混合信号的精确平动补偿.以累积残差为基础定义权重计算函数,再结合MCMC采样方法对补偿后的信号进行静态参数PF,实现了多维参数的同时估计,避免了误差传递影响,而且算法收敛效率较传统MH方法有明显提高.仿真和实验结果都证明了算法的有效性,体现了该算法对微动参数的精确估计能力,这有利于对微弱振动幅度目标的探测以及对微动参数接近的目标微动特征进行分辨.实际中往往存在多目标或多散射点产生的多分量混合信号,下一步将在此基础上针对多分量混合信号的参数估计开展研究.