基于声信号的饰面砖外墙面空鼓检测研究

胡媛馨 ，高建卫，孔 戈，徐春艳，薛伟明，张旭清，高蕴琪（.上海众材工程检测有限公司，上海009；.上海海事大学 海洋科学与工程学院，上海 006；.上海海事大学 信息工程学院，上海 006）

建筑外墙饰面层的空鼓、脱落不仅影响建筑物的视觉外观，还严重影响公共安全。对建筑物外墙饰面层进行检测，排查空鼓墙面，是一件急需解决的事情。本文运用声波振动测试样本采集方法，对饰面砖外墙面进行敲击信号采集，利用梅尔频率倒谱系数对采集样本进行特征提取和分析，并将隐马尔可夫模型应用于建筑外墙面饰面层空鼓检测中，实现声信号识别方法在外墙饰面层黏结空鼓缺陷上的应用。

1 声信号检测原理和模型

1.1 敲击声信号的预处理

墙饰面层敲击信号的声信号识别，需经过预加重、分帧、加窗和端点检测等几个预处理步骤，将声信号转变成数字信号，实现声信号的特征提取。

预处理过程及详细步骤见文献[1]。

1.2 梅尔频率倒谱系数

声信号分析主要是对提取的特征参数进行处理，得到体现信号本质的特征参数。本文采用梅尔频率倒谱系数（Mel-Frequency Cepstrum Coefficients，简称 MFCC）对建筑外墙敲击声信号进行分类，利用声音的音调特性进行特征提取，计算听觉主观频率上频谱的倒谱。MFCC 特征参数从本质上而言即为各个频带对应的能量特征[2-6]。

1.3 隐马尔可夫模型

隐马尔可夫模型（Hidden Markov Model，简称HMM），是由 Markov 链发展而成的。它可用一个五元组数来描述，即，将5个参数分别作如下定义[1]：

(1) N：隐马尔可夫模型的状态数，在实际中设定为固定值。设 N 个状态 θ1，θ2，……，θN，则 n 时刻 Markov链所处状态为 qn，qn∈(θ1，θ2，……，θN)。

(2)m：每个状态对应的可能观察值数目。记m 个观察值为 V1，V2，……，VM，t 时刻观察到的观察值为 Ot，Ot∈(V1，V2，……，VM)。

(3) π：初始状态概率矢量。π = (π1，π2，…，πN)，其中 πi= P(q1= θi)，1≤i≤N，πi表示 t =1时刻处于状态 θi的概率，并满足 ∑tπi= 1。

(4) A：状态转移概率矩阵。A=(aij)N×N，其中，aij=P(qt+1=θj│qt=θi)，1≤i,j≤N,aij为从状态 i 到状态 j 的概率，aij≥ 0，³i,j 且 ∑jaij= 1,³i。

(5) B：可观测序列概率分布矩阵。B=(bjk)N×M，其中，bjk=P(Ot=Vk│qt=θj)，1≤i，j≤N,1≤k≤N。

在计算过程中，N 和m 的值均保持不变，针对识别问题、解码问题和训练问题，隐马尔可夫模型分别有前向、后向、前向-后向算法，Viterbi 算法和 Baum-Welch 算法3种算法。根据墙体敲击声信号特征参数序列是随时间变化的，试验分析中采用的 HMM 模型为可以模拟时间序列的左-右模型。

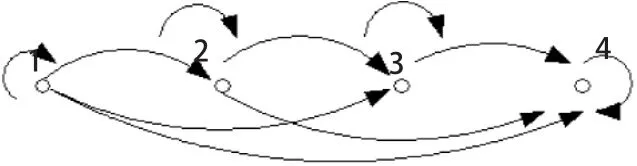
图1 HMM 左-右模型

2 试 验

2.1 试验目的

采集饰面砖外墙面敲击声信号，对其进行预处理和特征提取，建立饰面砖正常与空鼓状态的模型数据库，将已知的敲击声信号数据对 HMM 模型进行测试。敲击声信号识别系统框架如图2所示。

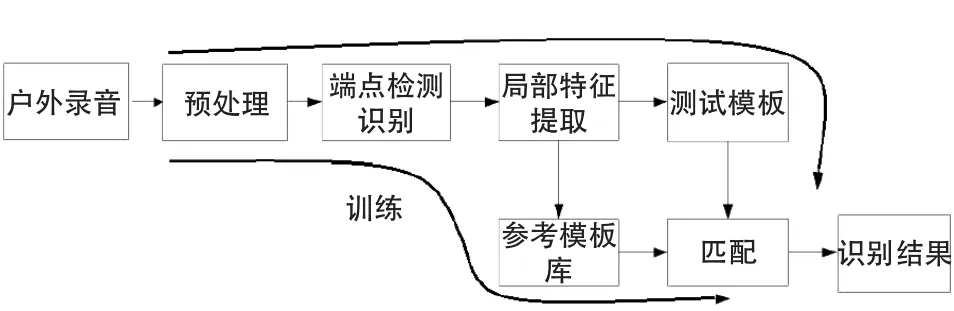
图2 敲击声信号识别系统框架图

2.2 试验概况

试验场地、仪器设备由上海众材工程检测有限公司提供。

2.2.1 试验设备

上海其高电子科技有限公司研发的 SignalPad 2016 测控软件、Type MP 40 声音传感器、USB-2405 凌华数据采集卡、敲击力锤、计算机。信号采集流程如图3所示。

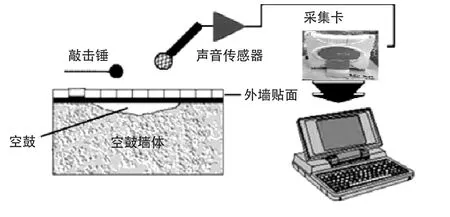
图3 信号采集流程

2.2.2 试验模型

试验模型及示意图如图4所示，参数见表1。

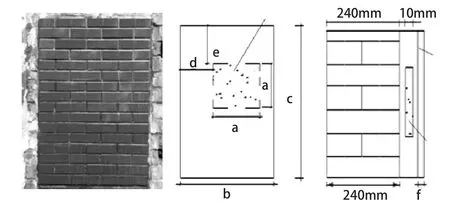
图4 饰面砖外墙试验墙及示意图

图4中，a 为空鼓缺陷尺寸长度；

b、c 为试验墙体的长度和宽度；

d 为试验墙体左边界距空鼓左边界的尺寸；

e 为试验墙体上边界距空鼓上边界的尺寸；

f 为饰面砖厚度。

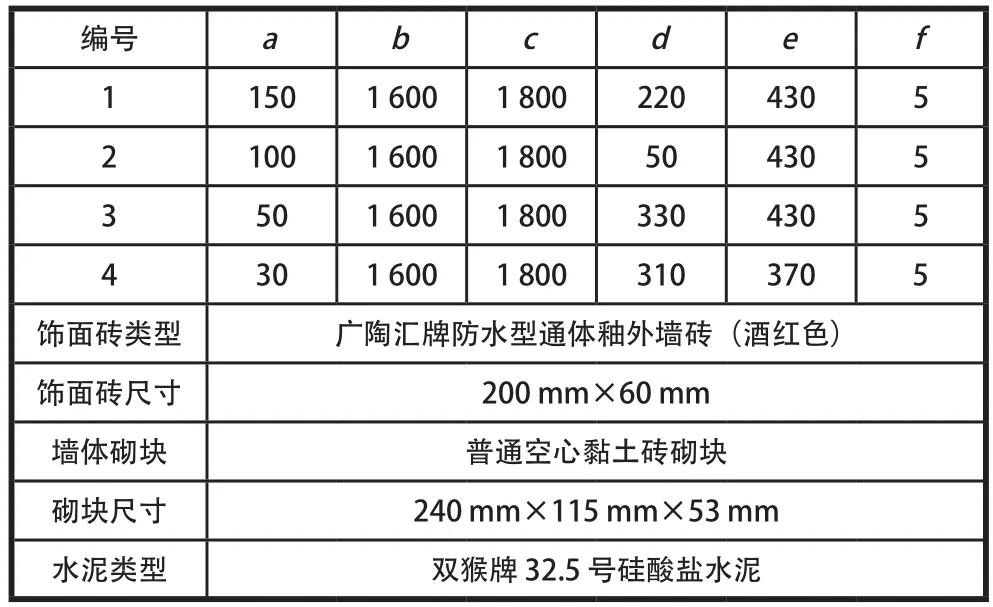
表1 饰面砖试验墙体参数 mm

2.2.3 试验方案

(1) 敲击点的位置分别位于空鼓中心、空鼓边缘及空鼓中心与边缘之间。空鼓区域具体的敲击位置如图5所示。

(2) 试验墙体饰面层黏结完毕之后，由于施工工艺、外界环境等因素产生的不规则空鼓，同样算作试验空鼓缺陷。

图5 饰面层空鼓区域敲击点

2.3 试验结果

敲击振动信号分为2类，第1类为正常饰面砖的敲击振动信号，第2类为空鼓饰面砖的敲击振动信号。

2.3.1 时域波形及频谱图

饰面层敲击分析结果如图6～图9所示。

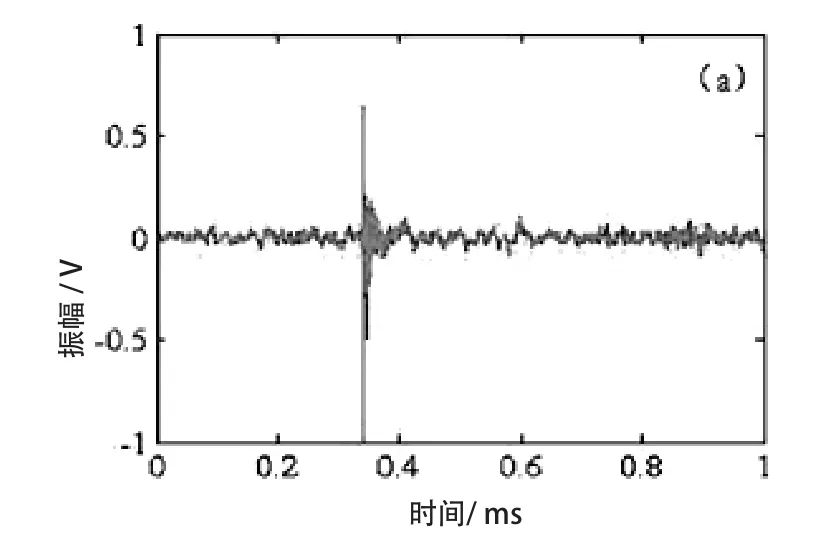
图6 正常饰面砖时域波形图

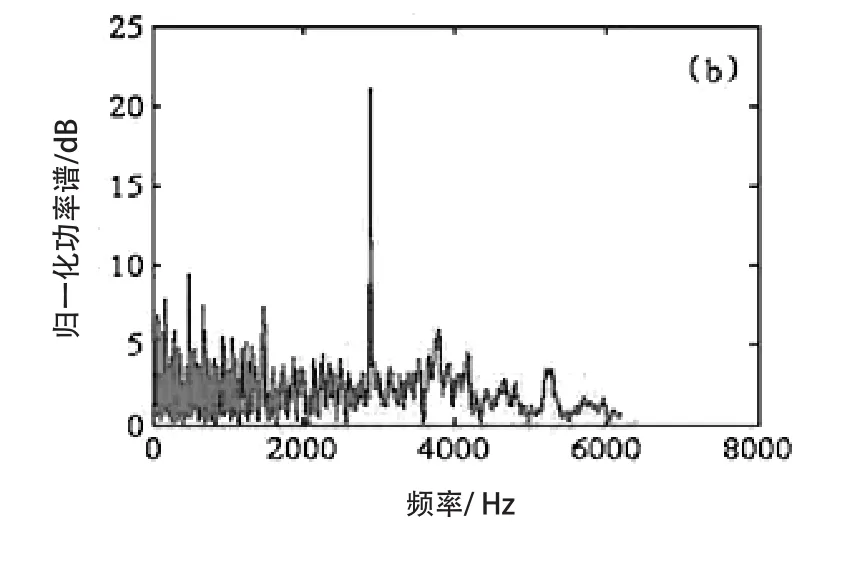
图7 正常饰面砖频谱图

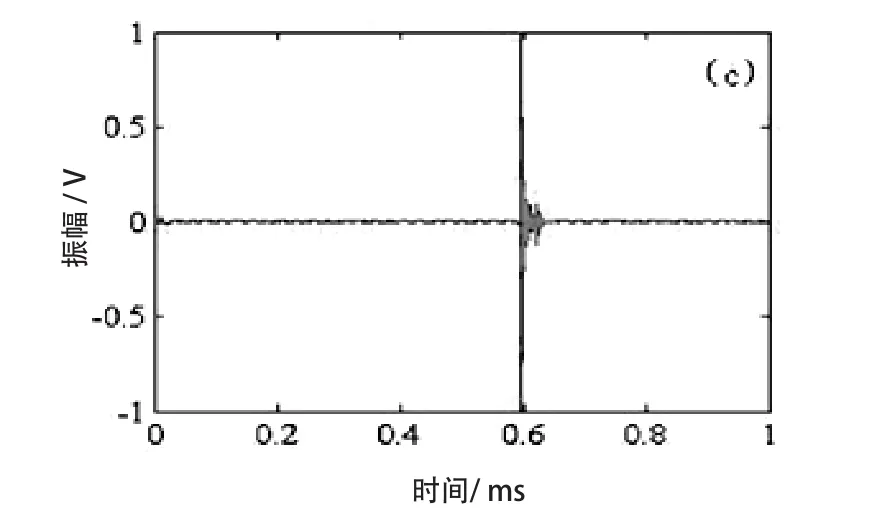
图8 空鼓饰面砖时域波形图

图9 空鼓饰面砖频谱图

正常饰面砖与空鼓饰面砖的时域波形图和频谱图明显不同：正常饰面砖的低频段能量所占比例较小，在 3000 Hz左右存在较高的能量，而空鼓饰面砖在 0～2000 Hz 存在较高的能量。

2.3.2 特征提取

采用 24 维特征参数对面砖饰面层敲击声信号进行特征提取，得到正常和空鼓饰面砖的 24 维 MFCC 特征参数矩阵三维图(图10、图11)。

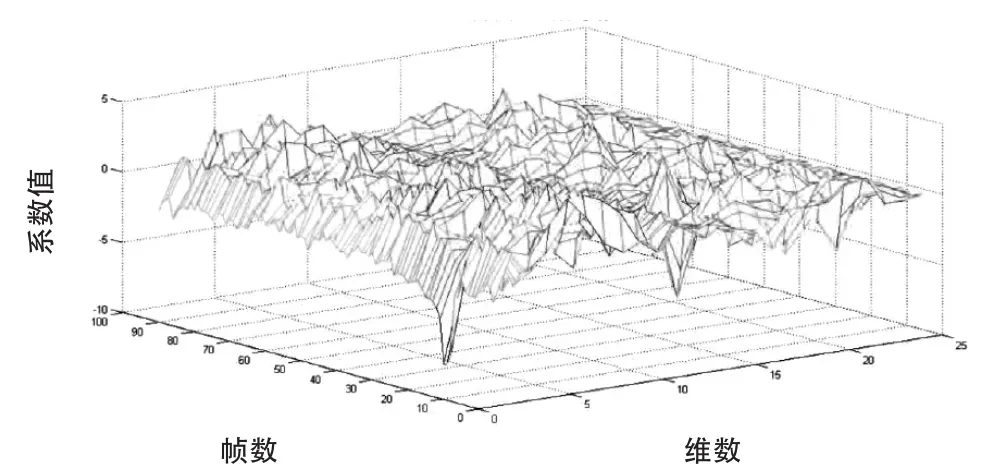
图10 正常饰面砖 MFCC 特征参数

图11 空鼓饰面砖 MFCC 特征参数

可以看出，正常饰面砖与空鼓饰面砖的 MFCC 特征矩阵在相同的帧数所对应的特征向量取值有较大的差异。该区别在模式识别算法中是将不同特征的声信号区分开来的依据。由此可见，MFCC 作为墙体敲击声信号识别的特征参数是可取的。

2.3.3 基于 HMM 的声信号识别分析

模式识别中，参考样本的数据量越大，样本所包含的特征信息越丰富，但实际检测时，在保证识别率的情况下，应尽量减少训练模型时需要的样本数据量。本文通过试验验证得到，HMM 模型的参考样本数与模型识别率之间的关系如表2 所示。

表2 HMM 模型识别率与参考样本数量的关系 %

取参考样本个数固定时对应的识别率的平均值为平均识别率，则 HMM 模型声信号平均识别率与参考样本个数的关系如图12所示。

图12 平均识别率与参考样本个数的关系根据 HMM 模型识别率

根据 HMM 模型识别率与样本个数的关系可知，样本个数> 20 时，识别率保持在 90% 以上。本文试验将 20 作为参考样本个数。

采集正常与空鼓饰面砖样本数据各 20 组，对采集的饰面层敲击信号进行预处理，提取敲击声信号的 MFCC 特征参数，再以敲击声信号的特征参数对隐马尔可夫模型进行训练，获得 HMM 模型。另采集正常和空鼓饰面砖样本数据各80 组，计算 HMM 模型产生相应样本观察值序列的概率，并利用 MATLAB 计算得到 HMM 模型的识别效率，结果如图13、图14、表3 所示。

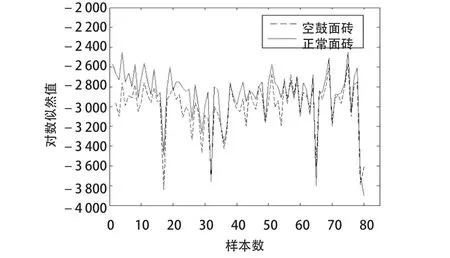
图13 正常饰面砖 HMM 识别结果

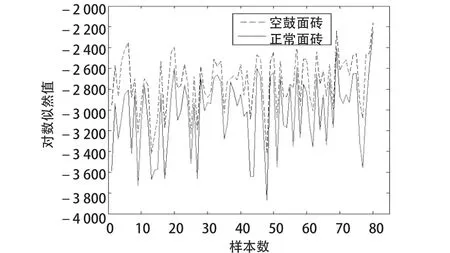
图14 空鼓饰面砖 HMM 识别结果

表3 HMM 的识别结果

由试验结果可知，相应状态的样本在其所对应的模型中产生的状态概率大于另一个样本的概率值；正常饰面砖65 组数据识别为正常，空鼓饰面砖 80 组数据全部识别为空鼓，识别率分别达到 81.25% 和 100%。试验证明 HMM 模型具有较高识别效率。

3 结 语

通过声信号识别技术对饰面砖外墙面空鼓黏结缺陷检测进行了试验研究，利用 MATLAB 语言和梅尔频率倒谱系数提取了饰面砖敲击声信号的特征参数、建立了 MFCC 特征参数数据库，结合隐马尔可夫模型识别算法，对模型识别率与参考样本个数的关系进行了探讨，并对3种空鼓缺陷尺寸、80组待测数据进行了 HMM 模型的声信号识别检测。

通过以上试验研究，验证了本文提出的基于声信号识别的饰面砖外墙面空鼓缺陷检测方法的可行性和准确性。该方法在实际工程应用中具有广阔前景。