制动器制动最高温度径向基神经网络预测

季景方，闫滕滕，王振雨



制动器制动最高温度径向基神经网络预测

季景方1，闫滕滕2，王振雨2

（1.汽车动力传动与电子控制湖北省重点实验室（湖北汽车工业学院），湖北 十堰 442002； 2.山推工程机械股份有限公司，山东 济宁 272000）

神经网络具有智能化和快速学习能力，在复杂动态系统预测方面具有十分广泛的应用，文章基于径向基函数神经网络，对制动器制动最高温度预测问题进行了研究。通过仿真模拟验证了径向基函数神经网络在逼近与预测方面的强大功能，同时通过对径向基函数分布密度的优化得到了用于制动器制动最高温度预测的神经网络预测系统，同时对制动温度的预测，得到了精度较高的预测结果。文章的研究对于制动器制动性能预测具有一定的参考。

径向基神经网络；制动器；预测模型；径向基函数分布密度

前言

制动器是汽车的关键零部件，制动性能直接影响到汽车的安全驾驶。对制动器进行多物理场耦合分析是有效的了解制动器制动性能的重要手段，但是借助于商业化的有限元软件仅仅可以分析在给定工况下的制动性能，同时由于制动器制动过程属于高度非线性过程，进行仿真的时间比较长，仿真过程中也存在不收敛的情况。采用商业化的有限元软件去完全了解制动器的制动性能是不现实的，同时技术难度比较大。人工神经网络（ANN）是在神经科学的基础上建立起来的，其具有快速学习和逼近复杂数学模型的能力，是当前进行复杂动态系统预测的重要手段。当前对于人工神经网络的研究成果很多，且取得了很大的突破。本文基于径向基神经网络，针对制动器制动过程中的最高温度预测进行研究。

1 径向基神经网络概述

径向基神经网络的逼近与预测的本质是在高维空间进行的插值，是一种新的神经网络学习手段。和BP网络不同的是，径向基神经网络属于前馈反向传播网络。径向基神经网络的结构如图1所示。

图1 径向基神经网络结构图

1.1 径向基层

径向基函数的第一部分是输入层到隐含层的非线性变换，其网络基函数为高斯函数，输出结果为。

径向基神经网络通过径向基函数有效的描述人类神经元的特性。结合高斯函数的数学特性可知，在中心区域附近，其网络的输出达到最大，而距离中心区域越远，其网络的输出也越小。网络输出变化的快慢由高斯函数的标准差来决定。高斯函数的标准差越小，其对输入的变化越敏感；高斯函数的标准差越大，其对输入的变化越不敏感。

1.2 输出层

径向基函数的第二部分是隐含层到输出层的线性加权过程，其网络的输出为。

其中，为隐含层和输出层之间的权重系数。

对于径向基神经网络来讲，尽管整体的网络输入到网络输出是非线性的，但是网络输出对于权重系数是线性的，因此权重系数可以通过求解非线性方程组得到，这样就使得径向基神经网络的学习速度加快，同时也有效的避免了其它类型网络在训练的过程中出现的局部最小问题。

2 径向基函数神经网络逼近与预测仿真

2.1 径向基神经网络逼近

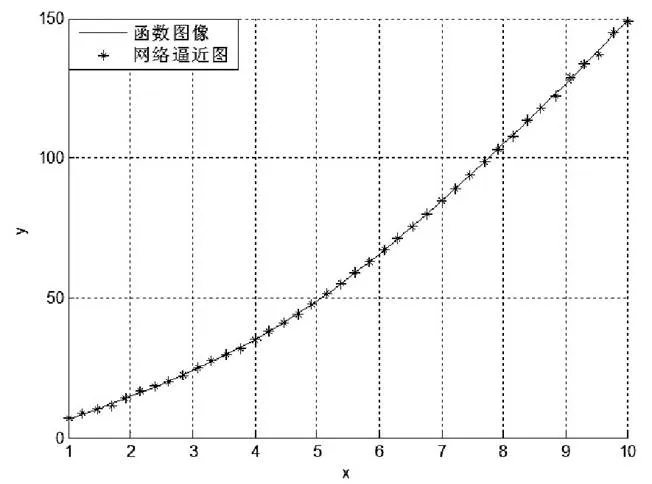
图2 径向基函数网络逼近图

由图2可见，采用径向基神经网络可以很好的对任意非线性函数进行逼近，其逼近效果良好。

2.2 径向基神经网络预测

采用径向基函数网络不仅仅可以对函数进行逼近，同时也可以进行预测。采用径向基神经网络进行预测的流程图如图3所示。

图3 径向基神经网络预测流程图

采用径向基神经网络，预测数据为=[2 8]，得到的预测结果和真实结果进行对比，对比结果如表1所示。

表1 网络预测结果与真实值对比

由表1可知，采用径向基神经网络可以很好的对任意非线性函数进行预测，得到的预测精度高且训练的时间短。

3 制动器制动最高温度预测

3.1 影响制动最高温度的因素

影响制动器制动最高温度的因素主要包括两类，分别为制动器自身的几何参数和与制动器边界相关的参数。本文主要是探讨制动器自身的几何参数与制动器制动最高温度的关系。制动器自身的几何参数包括摩擦片的包角、摩擦片的内径、摩擦片的厚度、制动盘的外径以及制动盘的厚度。由于制动盘的包角、摩擦盘厚度、摩擦片内径、摩擦片厚度、制动盘外径、制动盘厚度数值差别比较大，因此在进行网络训练之前需要对数据进行归一化处理。对于数据归一化处理的方法有很多种，本文采用公式（3）进行归一化处理，将所有的数据转化到区间[-1 1]上。

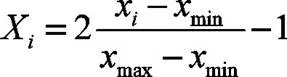
3.2 网络训练测试和预测

借助参考文献[2]中的数据进行制动器制动最高温度预测的研究，将前14组数据作为径向基神经网络训练数据，15-17组数据作为测试网络数据，得到测试数据和实际制动最高温度的误差，结果如表2所示。

表2 网络测试结果误差表

通过训练数据得到用于预测的径向基神经网络。在实际训练网络的过程中通过增加训练数据和调整径向基函数的分布密度来不断的提高网络的预测精度。本文搭建的用于制动器制动最高温度预测的径向基神经网络，其径向基函数分布密度为1.2。测试数据的最大误差控制在5%以内。将训练好的径向基神经网络用于制动器制动最高温度的预测中，其预测值和实际的误差结果如表3所示。

表3 网络预测结果误差表

由表3可见，本文搭建的制动器制动最高温度径向基神经网络系统可以很好的对制动器最高温度进行预测，其预测的精度满足实际工程需要。

4 结论

通过对径向基神经网络基础理论的分析，给出了搭建径向基函数神经网络的流程，同时通过模拟仿真验证了径向基函数神经网络对于函数的逼近与预测具有良好的性能。将制动器制动最高温度数据分为训练数据和测试数据，通过对径向基函数分布密度的优化，得到了预测制动器制动最高温度的神经网络系统，同时借助于该径向基函数神经网络系统进行预测，其制动最高温度预测结果预测为0.47%。本文的研究对于制动器制动最高温度的预测研究具有一定的参考价值。

[1] 芦有鹏,杨菊.基于径向基神经网络的交通出行预测[J].兰州交通大学学报,2018,37(02):27-42.

[2] 张磊.盘式制动器热结构耦合分析及制动性能优化[D].吉林大学,2012.

[3] 周星勇.径向基神经网络在地铁沉降预测当中的应用[J].科技资讯,2017,15(20):93-94.

[4] 杨玥. 基于神经网络的盘式制动器热—结构有限元分析结果预测模型研究[D].吉林大学,2013.

[5] 秦富,聂建华,胡瑾.基于主元分析的径向基神经网络预测模型研究[J].工业控制计算机,2015,28(02):59-60.

Prediction of brake maximum temperature based on radial basis function neural network

Ji Jingfang1, Yan Tengteng2, Wang Zhenyu2

( 1.Laboratory of Automotive Power Train and Electronics Hubei University of Automotive Technology, Hubei Shiyan 442002; 2.Shantui Construction Machinery CO., LTD, Shandong Jining 272000 )

The neural network has the ability of intelligent and fast learning and is widely used in the prediction of complex dynamic systems. Based on radial basis function neural network, this paper studies the problem of braking maximum temperature prediction. The powerful function of radial basis function neural network is verified for approximation and prediction by simulation. At the same time, the neural network prediction system used to predict the brake maximum temperature is obtained by optimizing the distribution density of radial basis function, and the obtained prediction results has a high precision for braking temperature prediction. The research has some reference for brake performance prediction.

radial basis function neural network; brake; prediction model; radial basis function distribution density

U463.5

A

1671-7988(2018)16-55-03

A

1671-7988(2018)16-55-03

CLC NO.: U463.5

季景方，（1986-），男，硕士，助教，研究方向：汽车零部件设计和力学分析。项目基金：汽车动力传动与电子控制湖北省重点实验室创新基金项目（2015XTZX043）。

10.16638/j.cnki.1671-7988.2018.16.020