汽车电控液压助力转向系统的建模及仿真

魏芳，张学文，王满力



汽车电控液压助力转向系统的建模及仿真

魏芳，张学文，王满力

（长安大学汽车学院，陕西 西安 710064）

为了进一步研究电控液压助力转向系统的性能，以BZZ型液压转向器为研究对象，通过对电控液压助力转向系统的研究，建立了转向油泵、全液压转向器等部件的数学模型，根据数学模型对各元件进行了特性分析；基于MATLAB/SIMULINK模块对电控液压助力转向系统进行了仿真，并且加入了PID控制算法调节，使得所建系统的仿真结果响应速度快，转向精度高，得到满足实际工作要求的性能。

电控液压助力转向；数学模型；仿真；MATLAB/SIMULINK

1 前言

近年来，随着汽车技术的迅猛发展，汽车保有量的不断增加，造成了非常复杂的交通状况，使驾驶员操纵转向盘的次数越来越多，对汽车转向操纵性能的要求也不断提高，这就需要不断提高转向系统轻便性、灵活性和其他有利于减缓驾驶员疲劳的系统性能，使驾驶员在停车时转动转向盘也能操纵自如，在高速行车时不会有飘的感觉。

2 EHPS的数学模型

2.1 液压部分数学模型

对于液压部分，将它分成三个部分分别建立子系统：全液压转向器、转向机构和转向油缸，然后再整合成整个系统的模型。

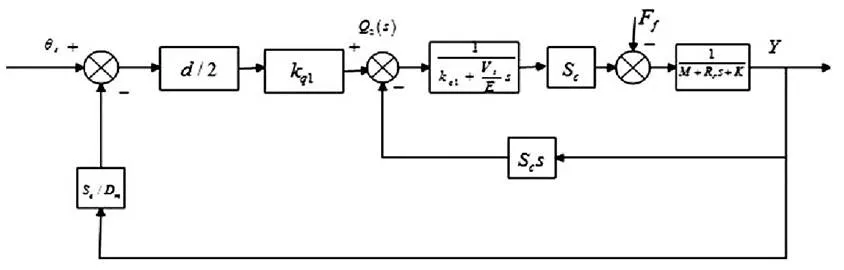
图1 液压系统方框图

由方框图化简可以得到液压系统的数学模型为：

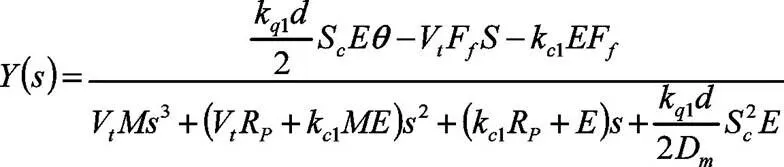
2.2 电控部分的数学模型

2.2.1 ECU的数学模型

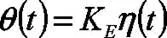
2.2.2步进电机的数学模型

本文中，把步进电机近似为一个比例环节。在系统中，步进电机的输入为脉冲频率，输出为角速度ω，步进电机的步距角为θ时，有：

那么步进电机的传递函数为：

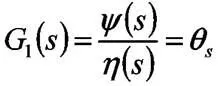
2.2.3电磁旋转助力器的数学模型

电磁旋转助力器产生电磁助力的原理就是利用通电线圈在磁场中的受力[2]。故有式=。

其输出力F的大小主要还是依靠电流I来确定。其数学模型如下所示：

2.3 电控液压助力转向系统的数学模型

通过之前分别对液压部分和电控部分的建模分析，可以得出整个EHPS方框图如下图2所示。

图2 整个EHPS方框图

本文中，将电控部分的3个模型都近似成为了比例环节。增益系数K为0.0203，步进电机的实际步距角θ为0.225度，电磁旋转助力器的增益系数K等于0.07。转向器的增益系数k1为0.82（2/），转向机构增益K为284度/米，由上可以得出电控液压助力转向系统以θ为输入，θ为输出的闭环传递函数为：

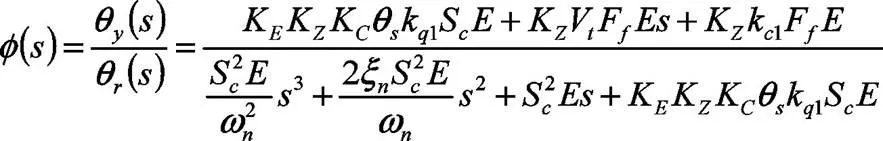
3 电控液压助力转向系统的仿真分析

3.1 转向系统的参数计算

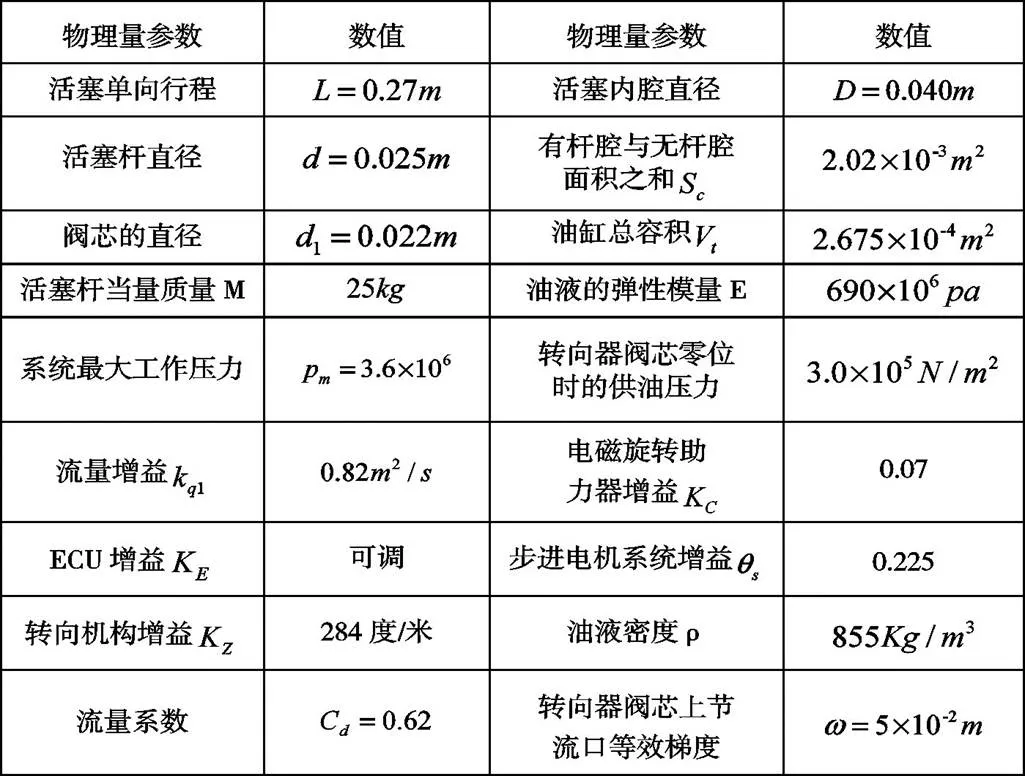
为了确定数学模型，需要对本系统中的各个参数进行确定及说明，采用BZZ型全液压转向器（其他参数由选件标准决定）。

表1 仿真系统数学模型的主要参数

3.1.1单个油缸总容V：

3.1.2油缸中有杆腔与无杆腔的面积之和S：

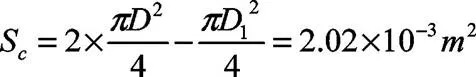
3.1.3忽略管道中的油液质量，液压固有频率ω：

随着转向器阀芯和阀套的开口变化，ζ也会随着产生较大的变化[4]，变化程度可达二三十倍之大，实际测量的。所以，要更正其计算值以得到更好的精确度，故取ζ=0.3。

3.1.5 BZZ1 E80流量

3.1.6流量增益

3.2 仿真系统的瞬态响应分析

根据上面计算的参数和设定的参数，可以得到参数化的系统方框图如图3所示：

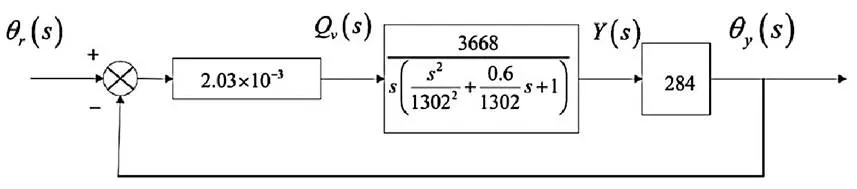
图3 参数化的系统框图

系统的开环传递函数为：

系统的闭环函数带入参数为：

阶跃的响应如图4所示：

图4 阶跃响应

从阶跃响应上看，上升时间过长，系统相应比较慢，所以要调整上升时间，加入PID校正，做进一步调试。系统在校正之前不能满足对转向系统的响应要求，所以，必须对系统进行校正。

3.3 仿真系统PID调节

PID控制器的传递函数为：

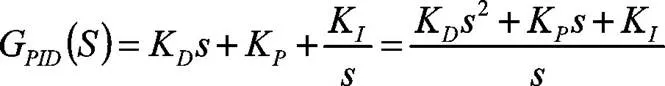
根据以上传递函数得出带PID控制器的闭环转向控制图如下图5所示：

通过对液压部分和电控部分的分别建模分析后，整合出整个EHPS的数学模型，利用整个EHPS的数学模型，采用MATLAB/SIMULINK，建立了EHPS的仿真模型。

图6 PID校正的参数化模型

如图（6）是系统经过PID校正之后的仿真模型，经过多次分析对比，可知当K=60，K=0.5，K=0.1时，系统的闭环传递函数为：G=18.94/(5.89e-007 s^3 + 0.000581 s^2 + s + 18.94)，这时的单位阶跃信号相应如图（7）所示：

图7 PID校正后的阶跃响应图

此时响应时间较长，安全性不高，所以还需调试。在command window输入如下指令更改scope图的背景颜色及曲线颜色，使其能够更清晰的显示响应的效果。

set (0,'ShowHiddenHandles','On')

set (gcf,'menubar','figure')

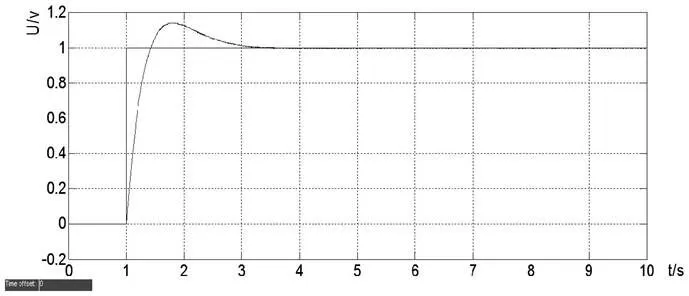
图8 修正参数后的响应

修正参数后的响应时间得到了改善，小于1s。

如下图9是PID校正后系统对正弦信号的响应：

图9 系统追正弦信号的响应图

由图9可知，现在系统的跟随性并不好，需要对系统进行调试。继续调整PID的控制参数，得到如下图10的结果：

图10 再次调试PID后系统对正弦信号的响应

将PID前的增益改为0.54，通过仿真结果可以看出，经过调试之后，系统对信号的跟踪能力得到了明显的加强，当输入发生变化时，系统响应较快，能够快速调整到设定角度处，虽然目前的转向系统通过ECU及其他执行机构组成后精度较高，但是相应的控制策略仍然是增强其工作性能的关键。

4 总结

在控制方面，综合实际情况，将PID应用到了系统中，在方向盘转角阶跃输入下，EHPS响应的速度得到了提高，同时也提高了其跟随精度。在进行PID控制的过程中，为了得到使系统性能达到更好的效果，通过大量的参数测试，结果表明系统在K=60，K=0.5和K=0.10时对阶跃信号和正弦信号反应速度快，转向精度高。

[1] 张君君.电控液压助力转向系统的设计研究[D].江苏大学,2009.

[2] 陈可.电磁式助力转向系统的性能分析与仿真[D].武汉理工大学,2005.

[3] 李锦.负荷传感型全液压转向系统的数学模型及试验验证[J].农业装备与车辆工程,2011(02):28-31.

[4] 王同建.装载机线控转向技术研究[D].吉林大学,2006.

Modeling and Simulation of Electro-Hydraulic Power Steering System

Wei Fang, Zhang Xuewen, Wang Manli

( University of changan automobile institute, Shaanxi Xi’an 710064 )

In order to further study the performance of the Electric-Hydraulic Power Steering System,taking BZZ type hydraulic steering gear as the research object.Based on the research of the Electric-Hydraulic Power Steering System, the mathematical model of the steering oil pump and the full hydraulic steering gear is established.The characteristics of the components are analyzed according to the mathematical model.Electric-Hydraulic Power Steering Systemis simulated based on the MATLAB/SIMULINK module. And join the PID control algorithm. Simulation results made of the system have high response speed and high precision.The system meet the requirements of actual work performance.

Mathematicalmodel; Simulation; MATLAB/SIMULINK; ElectricHydraulic Power Steering

B

1671-7988(2018)16-19-03

U462.3

B

1671-7988(2018)16-19-03

CLC NO.: U462.3

魏芳（1994-），女，长安大学汽车学院车辆工程专业硕士研究生在读；张学文（1993-），男，长安大学汽车学院车辆工程专业硕士研究生在读；王满力（1992-），男，长安大学汽车学院车辆工程专业硕士研究生在读。

10.16638/j.cnki.1671-7988.2018.16.007