水泥混凝土路面接缝错台转换模型构建分析

（山东省交通科学研究院， 山东 济南 250014）

0 引言

道路交通荷载的不断增加，导致当前水泥混凝土路面逐渐出现开裂、接缝材料剥落、错台、断角等损伤。对于错台模型的相关研究，国外通常使用平均量指标，但对于以路段为基础的错台量计算构建，则主要包括对路龄、荷载、结构参数等参数的发展预估。与国外相比，我国对于接缝错台模型的研究较为缺乏。近年来，我国部分道路工作者基于国家交通科技项目蓬勃发展的背景，对接缝错台模型展开了一系列的攻关研究。并且与以往多基于错台发生数量和长度采集相关数据并进行分析不同，随着快速检测手段的普及与推广，目前主要采用测试车自动采集计算错台量的方式，从而规避了缺乏预测性这一不足，并成为当前主要的维护方式。

1 模型概况

1.1 性能预测模型发展

建立性能模型最开始以经验为基础，后来逐渐过渡到力学型或力学与经验结合的模式，实现了从静态到动态的转变。以单项指标为基础对接缝错台性能模型进行研究，最开始以美国研究者为主，他们最早对一般路段的数据进行分析之后，建立起最初的公路战略研究模型[1]，并在此后又建立了美国混凝土铺面协会模型，在力学与经验结合的基础上创建接缝错台模型。另外，还有学者通过建立刚性路面性能与修复计划模型的方式，研究了接缝错台模型的构建策略。上世纪末，两名学者在前人的基础上，建立了以性能为基础的规范化模型，此模型以综合指标为基础，具有较高实用价值，适合多种路面损伤研究。国内学者所展开的相关研究，由唐伯明等学者开始，他们根据浙江省路段多年的监测资料，建立了疲劳开裂模型体系，从而建立起断板率模型。毕艳祥等研究者在积累了上海道路管理系统的数据后，采用专家调查法最终得出路面经验寿命的结论。

1.2 错台模型综合分析

接缝错台模型主要分为经验型、力学型和力学与经验结合型。在经验型中，代表模型为美国公路战略研究计划和刚性路面性能与修复计划；在力学与经验结合型中，包括美国混凝土铺面协会、美国路面成本模型、路面长期性能计划以及基于性能的标准模型（2.0与3.0版本）[2]。不同的错台模型采用了不同的计算方式，相关参数也有所区别。

1.3 基层参数不断细化

在研究了水泥混凝土路面的错台情况后，了解到影响错台信息的主要因素在于路面基层材料的抗冲刷能力，而基层类型对于路面接缝的错台会产生非常关键的影响，因此基层相关参数都是错台的影响因素[3]。在基层类型的分类上，最早的美国公路战略研究计划并未分类，而之后不久的刚性路面与修复计划则主要分为稳定与非稳定类，美国混凝土路面协会将其分为稳定类和未处治类，美国国家路面成本模型则将其分为腐蚀与非腐蚀类两种，最新的路面长期性能计划则将其分为四大类，即贫混凝土、ATB基层、CTB基层和未处治类。

1.4 模型参数的隐性化

根据经验模型逐渐向力学与经验结合模型的进展来看，在经验型的模型中，大多参数为非力学参数，并且通常借助显式参数方式在模型中得以直接表现，因此方程式往往非常复杂且混乱，关键点很难突出。力学与经验结合的模型中，引入了部分力学因子，因此大量的非力学参数转变为隐式参数，最终简化了计算公式，使重点得以显著突出[4]。

2 转换模型构建

2.1 错台分布状况

以我国A省某高速路段作为研究对象，通过研究发现，水泥混凝土路面的双向四车道外侧与内侧车道在错台的分布上区别十分明显。为了方便对数据参数进行比较与分析，在内、外两个车道以及上下行方向上，均对数据完整的路段予以保留，对于部分路段而言，仅存在一个方向或部分车道才具有的数据时，则需要根据实际情况进行针对性处理[5]。总的来说，错台的数量与车道和行车方向有关：从车道来看，不管上行或是下行的方向，发生错台的部位更多偏外侧，内侧车道通常不容易出现错台，但上行方向的内侧车道不同公里段的错台数量没有显著变化，下行方向则具有非常明显的差异；从行车方向上来看，不管内外车道，处于上行方向的错台发生率显著较低，但减少的幅度则不如按车道分析的明显，尤其在外侧的车道方面，上下行方向发生错台的差异显著性更低[6]。

2.2 点对点直接转换

对于数据类型的转换，首先不引入其它的任何参数项目，根据过去采集的错台数据和每公里自动采集并输出的平均错台量之间的散点图，将其初步拟合成线性关系，从而方便观察、理解和计算，能够直接将错台数转化为平均错台量[7]。将数据带入到统计学软件中进行一元线性回归分析，得到的错台数据为线性回归模型，表达式为：

平均错台量用表示，单位为“mm”；错台数量用表示，单位为“处”。

再次以统计学软件分析一元非线性对于数的回归结果，能够得到错台的数据类型，分析其对数回归模型，表达式为：根据公式可以发现，直接转换的关系式当中，线性回归式与对数回归式之间都不具有较大数值的相关系数[8]。但如果错台数量太小，则线性回归式的初始错台量就会偏高，而这一结果并不符合工程所能允许的数值。因此，通过上述公式确定系数及其合理性时，则更应考虑使用对数模型[9]。

2.3 引入交通量参数的转换

首先是交通量的调查分析。在混合交通量的车型比例方面，以GH高速GL段在进行大修之前的交通量进行调查，整理得到的调查结果，得到的混合交通各车型的车辆数如表 1所示。在混合交通量的方向系数与车道的分布比例方面，上行与下行方向在车辆的分配上大体为等比例，内车道与外车道各型车分配的比例如表 2所示。在当量轴载换算的原则方面，收费站的称重记录无法获取，因此不同车型在实际载重量或空载、半载以及满载、超载各类型的比例也无从得知。根据我国的超限治理规定，再结合GH高速的GL段在维修过程中所运用的标准轴承折算方式，不计小客车、普通轿车，对大客车以及两轴车以标准轴计算，对三轴与四轴则分别按照三个与四个标准轴计算，对于五轴与六轴则都按照五个标准轴进行计算，最终得到100kN的标准轴载累计的作用次数。

表1 混合交通的不同车型数量比例

表2 车道的分配系数

其次是选择模型的形式。根据平均错台量和错台数之间的关系散点进行分析，发现二者存在着某种线性关系，也可能存在对数关系。通过分析对比多种形式的模型后发现，平均错台量和累计的作用次数之间更偏向线性关系，因此可以初步判断，模型常用的两种公式有线性模型基本型式和非线性模型基本型式。线性模型的公式为：

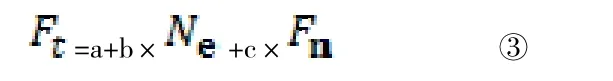
公式中的是累计标准轴载的作用次数，单位为百万次；a、b、c均为回归系数。

非线性模型的公式为：

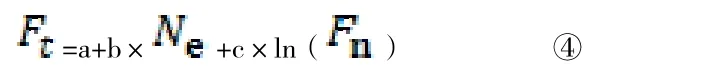
最后是确定模型的参数。通过统计学软件将导入的错台数据和交通量数据进行多元线性回归及多元非线性回归分析后，得到函数常数项与变量系数，方程式以⑤和⑥表示，具体如下：

多元线性模型的方程式，考虑累计交通量的影响，其错台转换后的多元线性模型公式为：

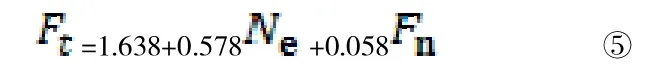
而多元非线性模型的方程式，考虑累计交通量的影响，其错台转换后的多元线性模型公式为：

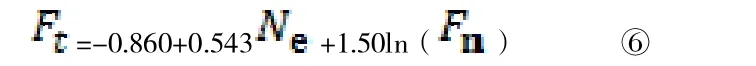
根据实践计算结果可以看出，在考虑引入了交通量变量后，得到的线性回归模型公式更加合理有效。

1. 模型变量与参数有效性检验

将数据带入到统计学软件中进行分析，首先考虑累计交通量以及错台数的变量，然后再通过逐步回归法分析整体结果，根据进入的顺序依次为错台数和累计交通量，所有变量均参与计算。根据计算结果，发现均为正值，因此与实际情况一样，错台量同错台数以及错台量同交通量均表现为正相关性。

3 结语

综上所述，本文得出如下结论：其一、在研究了不同的线性与非线性的模型之后，所得到的引入交通量对于多元线性错台转换模型的影响公式计算出的结果拟合效果更优，同时在构建模型时采用了大数据，不同参数之间不具有多重共线性，因此更符合实际；其二、在带入到统计学软件中进行计算后，更能保证数据的连续性，从而有效弥补了长期预测路面性能的过程中可能出现的间断问题，因此这也成为解决问题的根本性思路之一；其三、错台的表现根据车道和行车方向的不同而存在或多或少的差异，外车道更容易出现错台，下行方向也更容易出现错台；其四、转换的模型主要以A省GH高速的GL段路段区域气候及交通特点为基础，而其它考虑的因素还包括交通量与路龄等，之后需要将湿度、温度、人为因素以及路面结构等因素都考虑进来，从而确保这一模型能够适应更多地形地貌。

[1]陈富强,陈富坚,黄慧.水泥混凝土路面接缝错台转换模型构建研究[J].重庆交通大学学报(自然科学版),2016(05):70-73+91.

[2]李伟,沙爱民,孙朝云,郝雪丽.基于线结构光的水泥混凝土路面错台三维检测[J].同济大学学报(自然科学版),2015(07):1039-1044.

[3]梁育生,蔡报强.水泥混凝土路面常见病害分析及防治措施[J].科技创新导报,2017(23):41-43,45.

[4]朱伟.水泥混凝土路面板底脱空检测及防治[J].建材与装饰,2016(52):215-216.

[5]李琳,罗芳.高速公路水泥混凝土路面加铺层设计与应用研究[J].公路工程,2016(3):117-121.

[6]袁化葵.浅谈水泥混凝土路面的维修[J].建筑工程技术与设计,2016(28):725.

[7]李晶晶,王占锋.接缝水泥混凝土路面错台模型对比分析[J].交通科技与经济,2017(1):54-58.

[8]李志鹏,曹家丕.浅析公路工程路面接缝及处治措施[J].卷宗,2017(24):136-136.