直列六缸发动机激振力分析与仿真
2018-09-05朱玉田苏健君郑昌隆张攀登
朱玉田,苏健君,刘 钊,郑昌隆,张攀登
(同济大学 机械与能源工程学院,上海 201804)
近年来,随着健康意识和经济水平的不断提高,人们在选购车辆时更加关注汽车乘坐的舒适性.汽车的振动强度过大,会对乘坐舒适性、驾驶员和乘客的健康以及行驶安全性带来一系列的影响[1].汽车一定程度的振动和噪声若持续8 h,乘客将会面临危险[2].因此,在竞争激烈的汽车市场上,提高车辆噪声控制水平已成为新的竞争焦点和技术发展方向[3].发动机作为汽车的主要振动激振源之一,对汽车的乘坐舒适性和噪声、振动与声振粗糙度(Noise,Vibration,Harshness,NVH)特性有很大的影响[4].
发动机的激振力分析作为研究发动机振动特性的基础,虽然已有一定的研究成果,但仍有较大的提升空间.因此,针对惯性力引起的振动和缸压力引起的振动,建立单缸力学模型并分别推导出各激振力表达式,进而建立直列六缸发动机详细力学模型,根据各缸的相位差推导出直列六缸发动机各激振力表达式.以某排量为6.75 L的直列六缸发动机为例,计算并仿真得出各激振力图像.本文提出的发动机激振力分析方法将对发动机振动特性分析有一定帮助.
1 发动机振动激励源及作用对象
研究发动机振动时,主要关心其在低频范围内的振动特性[5].在低频范围内研究时,金属变形作用对振动影响较小,而弹性元件变形对振动对振动影响较大,因此,可将发动机视为由两个刚体组成:发动机缸体和曲轴及其联动部件,如图1所示.当曲轴与缸体的连接刚度较小时,运动构件对发动机缸体振动的作用较小,若为简化计算,可对发动机近似地进行6自由度建模.但当曲轴与缸体的连接刚度较大时,运动构件对发动机缸体振动的作用不可忽略,应将发动机视为一个7自由度的研究对象.

图1 发动机模型Fig.1 Engine model
如图2所示,发动机振动的激励主要来自于两个方面:① 发动机内部运动构件运动时产生的惯性力和惯性力矩;② 发动机气缸内部气体燃烧产生的周期性作用力[6-7].除此之外,发动机内部的摩擦也会产生激振力,效果不明显,所以忽略不计.
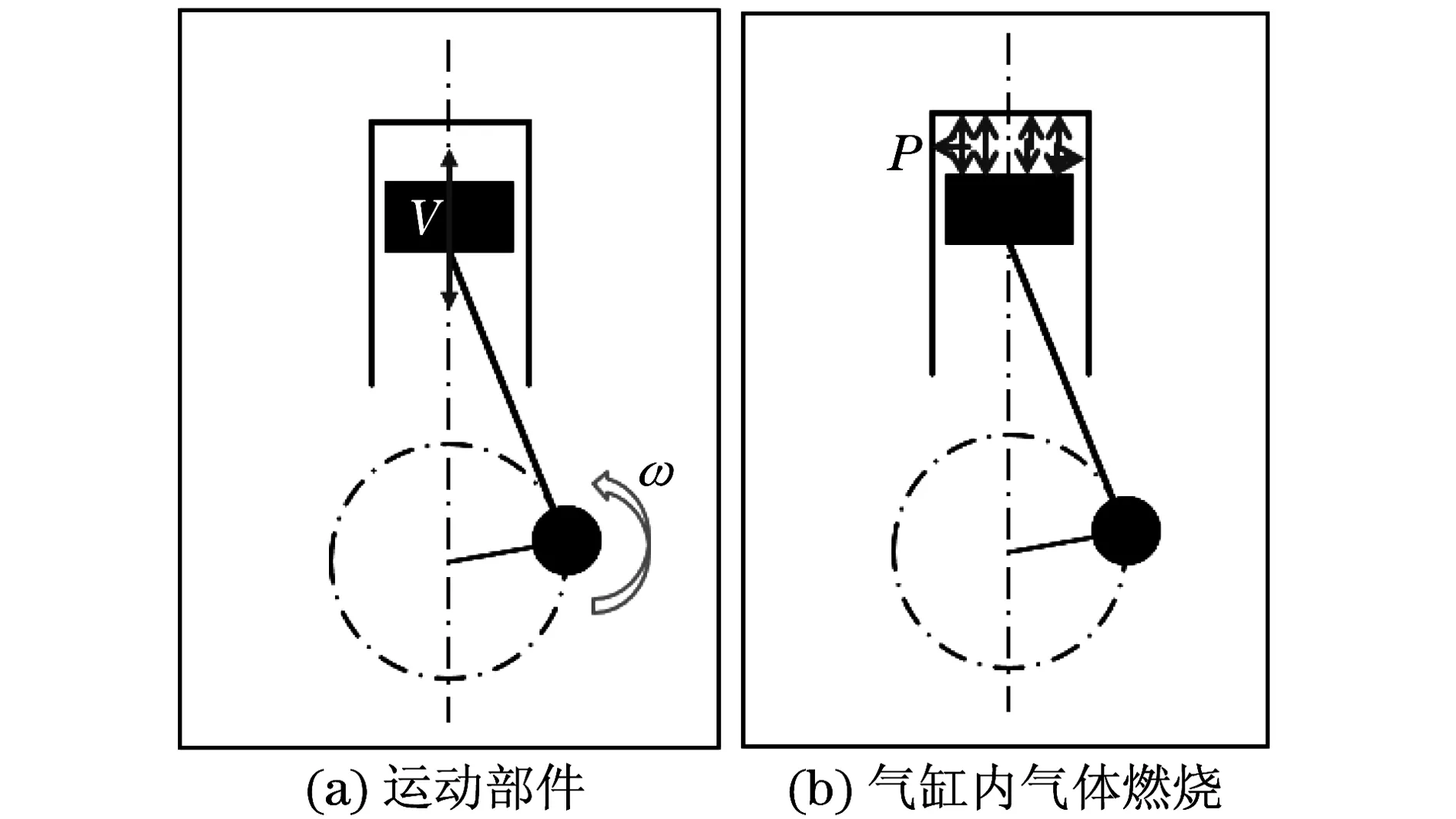
图2 发动机激励的产生原因Fig.2 Causes of engine excitation
如图3所示,发动机的每种激励都会产生两种作用:① 作用在发动机缸体上,对整体产生激振力和力矩;② 使曲轴及其联动部件与缸体产生相对运动.
运动构件产生的惯性力作用在运动构件上,通过内部的约束力传递到缸体,对发动机整机产生力和力矩(称为惯性激励力及力矩),其反作用力和惯性力一起构成对运动构件的驱动力矩(称为惯性驱动力矩).惯性驱动力矩为一对大小相等、方向相反的力矩,分别作用于曲轴和缸体上.发动机气缸内部气体燃烧产生的周期性作用力作用在发动机缸体上的力,称为缸压激振力;使曲轴及其联动部件与缸体相对运动的力矩,称为缸压驱动力矩.缸压激振力通过发动机内部各元件的约束力相互抵消为零.缸压驱动力矩为一对大小相等、方向相反的力矩,分别作用于曲轴和缸体上.
综上,根据激振源和激振作用的不同,将激振力分为4个类别来计算,其命名总结如表1所示.

表1 发动机激振力分类Tab.1 Classification of engine’s exciting forces
2 惯性力引起的激振力及力矩
2.1 惯性激振力的初步分析
直列六缸发动机的结构如图4所示,建立xyz空间坐标系.发动机内部运动部件的运动对整体产生的效果,可用6个分量来表达,即Fx,Fy,Fz,Mx,My,Mz,分析发动机的惯性激振力如下:
(1) 发动机中产生惯性力的主要部件包括活塞和连杆;
(2) 因为惯性运动都是平行于yOz平面,所以不会有x方向惯性力,即Fx为0;由于直列六缸发动机的对称性,y方向的惯性力也可以抵消掉,使得对x轴、z轴不会产生惯性扭矩,即Fy,Mx,Mz为0;当取坐标原点为曲轴中心点时My为0.

图4 直列六缸发动机Fig.4 L6 engine
综上,主要分析Fz.
2.2 惯性激振力及惯性驱动力矩的计算
如图5所示,分析单缸惯性力和力矩.AB为连杆,BO为曲柄,A处为活塞,质量为m0,A′为活塞上止点.曲柄的旋转带动活塞进行往复运动,连杆简化为质量集中于两端的模型,质量为m1,m2,假设AB为l,BO为r,AB与中心轴夹角为β,BO与中心轴夹角为θ,下面对模型进行运动分析.
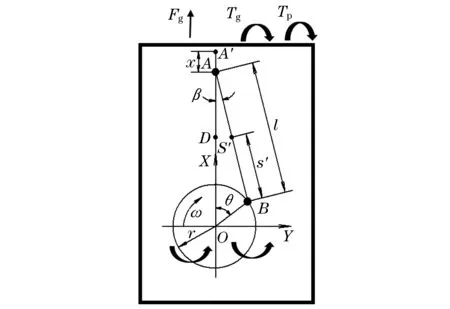
图5 单缸激振力分析模型Fig.5 Analysis model of exitingforces of single cylinder
对于曲柄机构的运动,根据模型中的几何关系,可以用连杆长度l和曲柄半径r,建立起曲轴转角θ和活塞行程x的运动关系:
(1)
惯性力Fg等于惯性质量mA乘加速度,惯性力中的质量mA包括活塞质量m0、连杆小头质量m1.
对于直列六缸:1缸和6缸的相位角相同,惯性力和惯性驱动力矩相同;2缸和5缸的相位角相同,与1缸的相位角相差120°;3缸和4缸的相位角相同,与1缸的相位角相差240°.
将θ+120°,θ+240°代入式(2)和式(3)中,即可求得Fg2,5,Fg3,4,Mg2,5,Mg3,4.六缸的惯性力合力为
(4)
六缸的惯性驱动合力矩为
(5)
3 缸压力引起的激振力
3.1 缸压模型
发动机4冲程包括进气行程、压缩行程、作功行程以及排气行程,每个行程对应曲轴旋转180°.对气缸内各行程压力分析如下:
(1) 进气行程.假设气缸进气压力变化是在气缸进气门打开的瞬时完成的,气体压力在行程中不发生变化,由于进气行程终了压力为0.075~0.090 MPa,暂时进气行程中气体压力取为0.080 MPa.
(2) 圧缩行程.气缸进排气门都关闭,将活塞之上的空间视为密闭空间,如果忽略压缩行程中气体温度的变化,可以将压缩行程中压力近似的视为与体积成反比,即
(6)
式中:a1为常数.
压缩行程的初始压力与进气行程终了压力相等,初始体积为活塞到下止点位置时气缸的体积.
(3) 作功行程.作功行程开始,由于气体的燃烧爆炸,缸内的温度急剧升高,所以缸内压力会有一个瞬变,压力瞬间增加至作功行程的最高压力.由于这个时间很短,将这一过程视为瞬间变化过程.变化后的压力取作功行程的最高压力3~5 MPa,这里暂取为4 MPa.
由于压力的升高,气体推动活塞从上止点开始向下运动,此时同样忽略气体内温度的变化,压力与体积的关系符合式(6).
压力的初始值为4 MPa,体积的初始值为活塞在上止点时气缸的体积.
(4) 排气行程.气缸的排气门打开,压力存在瞬间减小的过程,而后由于与大气接通,此时气缸内的压力视为不变,排气行程终了压力为0.105~0.115 MPa,取为0.110 MPa.
根据以上分析,建立气缸压力模型如图6所示.
3.2 缸压力引起的激振力
缸压激振力为发动机气缸内部气体燃烧产生的周期性作用力作用于发动机整体的激振力,其值为0.因此,主要分析缸压力对曲轴相对缸体回转振动的驱动力矩.
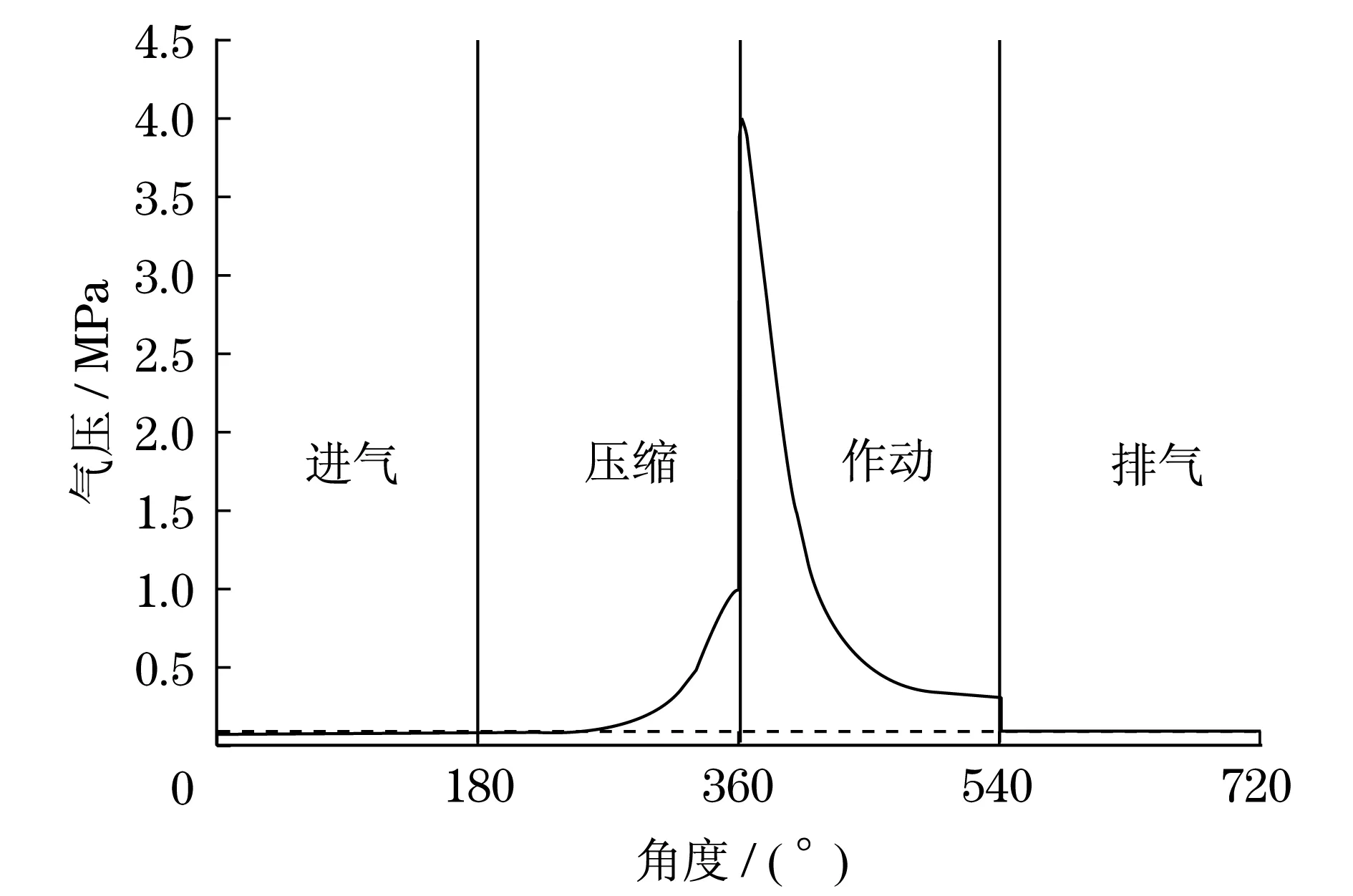
图6 气缸压力模型曲线Fig.6 Curve of cylinder pressure model
根据图6气缸压力模型,对单缸的驱动力矩进行分析.活塞受到气缸内气体的压力,压力的计算公式为
(7)
式中:S为活塞面积.
根据
(8)
式中:v为活塞往复运动速度;ω为曲轴转动角速度.可以计算出单缸的驱动力矩公式为
(9)
各缸相差120°相位差,将θ+i120°(i=1,2,…,5)代入式(9)中,即可求得Mq2~Mq6.因此,六缸的缸压驱动力矩公式为
(10)
4 直列六缸发动机激振力仿真
4.1 发动机型号及参数
仿真选用某排量为6.75L的直列六缸发动机,其参数如表2所示.
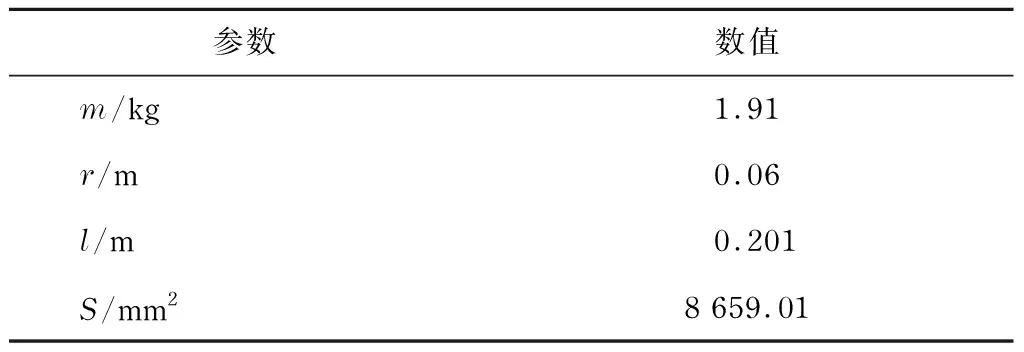
表2 某排量为6.75L的直列六缸发动机参数Tab.2 Parameters of a L6 engine
(11)
根据上述公式推导,仿真可得各缸惯性激振力如图7所示,六缸总惯性激振力如图8所示,各缸惯性驱动力矩如图9所示,六缸总惯性驱动力矩如图10所示,各缸缸压驱动力矩和总缸压驱动力矩如图11所示.
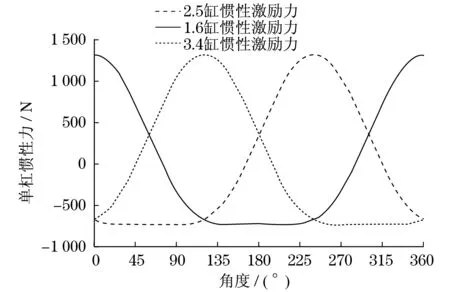
图7 各缸惯性激振力图线Fig.7 Inertia exciting force of each cylinder
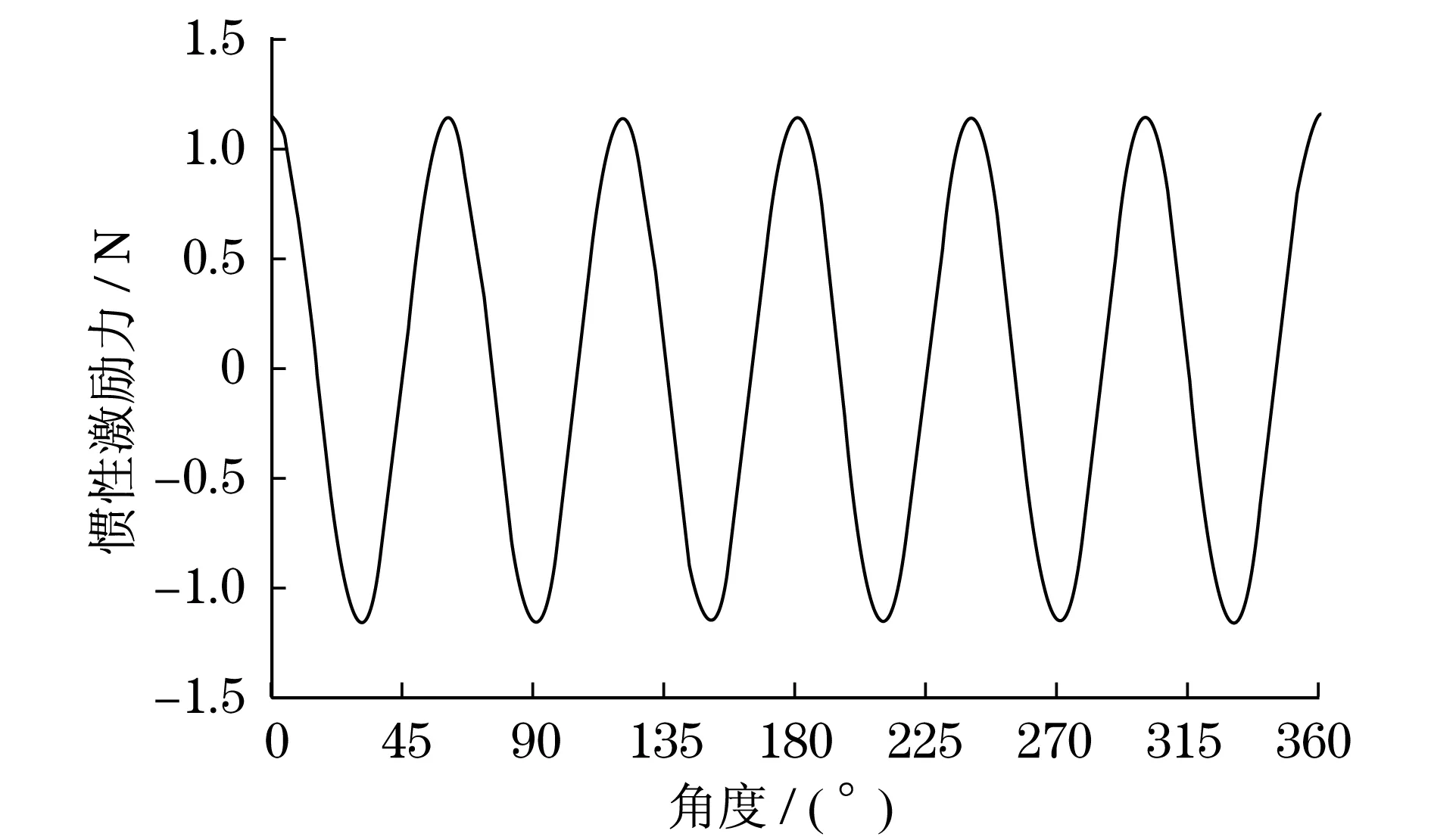
图8 总惯性激振力图线Fig.8 Total inertia exciting force
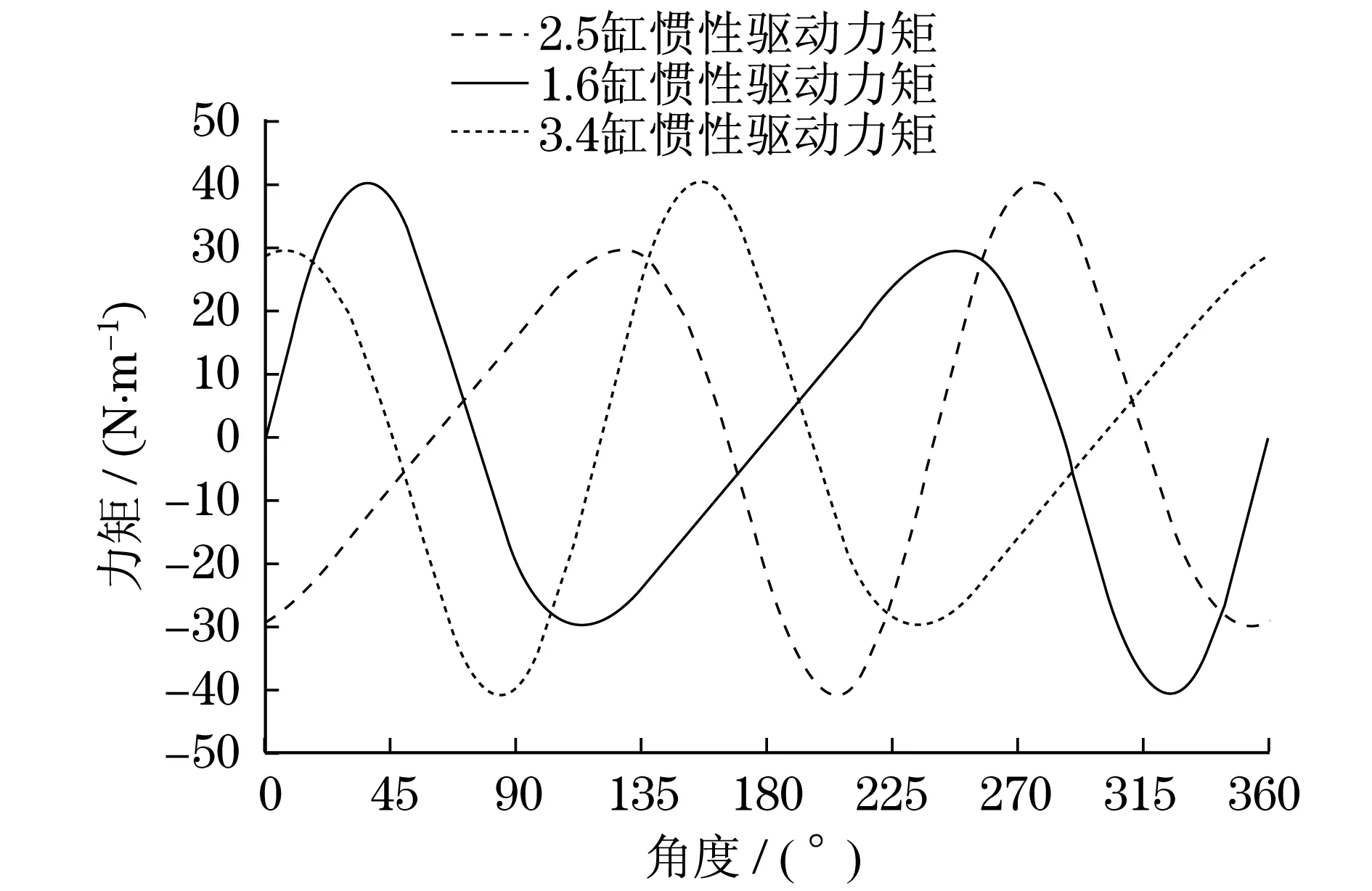
图9 各缸惯性驱动力矩图线Fig.9 Inertia driving torque of each cylinder
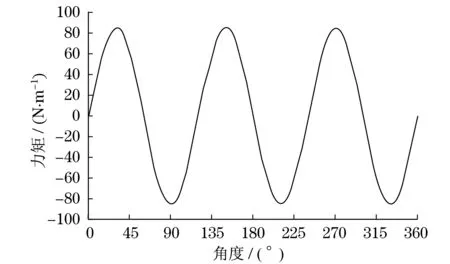
图10 总惯性驱动力矩图线Fig.10 Total inertia driving torque
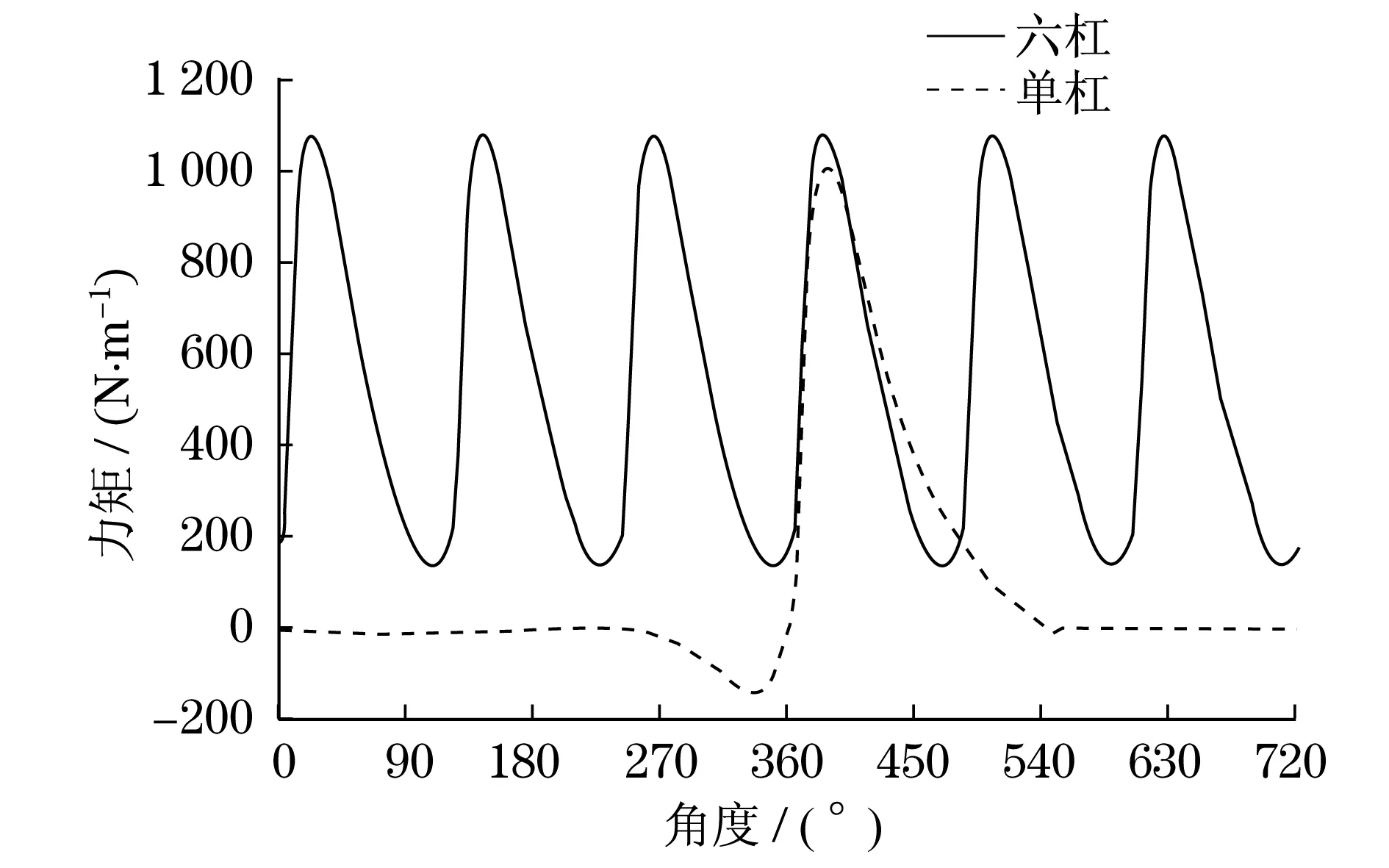
图11 缸压驱动力矩图线Fig.11 Cylinder pressure driving torque
5 结语
本文建立了发动机7自由度模型,根据激振源和激振作用的不同,分类分析了发动机激振力,从单缸出发推导其数学表达式,进一步推导出直列六缸发动机的各类激振力的数学表达式,并以某排量为6.75 L的直列六缸发动机为例子进行激振力仿真.该激振力分析方法将为发动机振动特性分析提供一定帮助.
