截面尺寸对伸缩臂屈曲失稳性能的影响

王俊飞,姚峰林,佘占蛟

(1.成都理工大学 工程技术学院,四川 乐山 614000; 2.太原科技大学 机械工程学院,太原 030024)

当前,起重设备为了满足大起重量和高起升度的实际需求,其伸缩臂的全伸长度越来越大.据大量起重机折臂事故统计分析,伸缩臂的失效不是强度不够,大多数事故是由伸缩臂屈曲失稳造成的,故保证伸缩臂的稳定性成为发展超大型起重机必须解决的问题之一[1-2].研究发现,影响伸缩臂屈曲临界载荷的因素很多,包括支撑方式、截面惯性矩、长度以及材料等,而当支撑方式、材料、长度确定时,对屈曲临界载荷影响最大的因素是截面惯性矩.本文通过分析截面尺寸对截面惯性矩的影响,进而分析出截面尺寸对伸缩臂屈曲临界载荷的影响.通过分析截面惯性矩与有限单元法相结合,以U型截面为例,分析了截面尺寸对伸缩臂屈曲失稳性能的影响,为工程设计提供参考.

1 截面尺寸对屈曲影响理论分析

在我国GB/T 3811—2008《起重机设计规范》中,给出了5节以下伸缩臂在变幅平面内和回转平面内的临界力计算公式(x轴与伸缩臂轴线重合,y,z轴分别位于回转平面、变幅平面内且与伸缩臂轴线垂直),其中回转平面的临界力为

(1)

式中:μ1为在回转平面内,由伸缩臂支撑方式决定的长度系数;μ2为在回转平面内,变截面伸缩臂长度系数;μ3为考虑起升绳影响的臂架长度系数;Iz1为基本臂对z轴的截面惯性矩；E为弹性模量.

变幅平面内的临界力为

(2)

式中:μ3为在变幅平面内,由伸缩臂支撑方式决定的长度系数;μ4为在变幅平面内,变截面伸缩臂长度系数;Iy1为基本臂对y轴的截面惯性矩;E为弹性模量.

由式(1)和式(2)可知,对I(截面惯性矩)的影响实际和对N(临界载荷)的影响是一致的,故本文先分析了截面尺寸对截面惯性矩的影响,再利用有限单元法研究截面尺寸对临界载荷的影响,彼此验证.

如图1所示,将U型截面划分为4部分.其中:①表示上盖板矩形截面;②表示圆弧过度截面;③表示腹板矩形截面;④表示下盖板半圆环截面.整个U型截面对z,y轴的惯性矩均可表示为4部分截面分别对z,y轴的惯性距之和,即

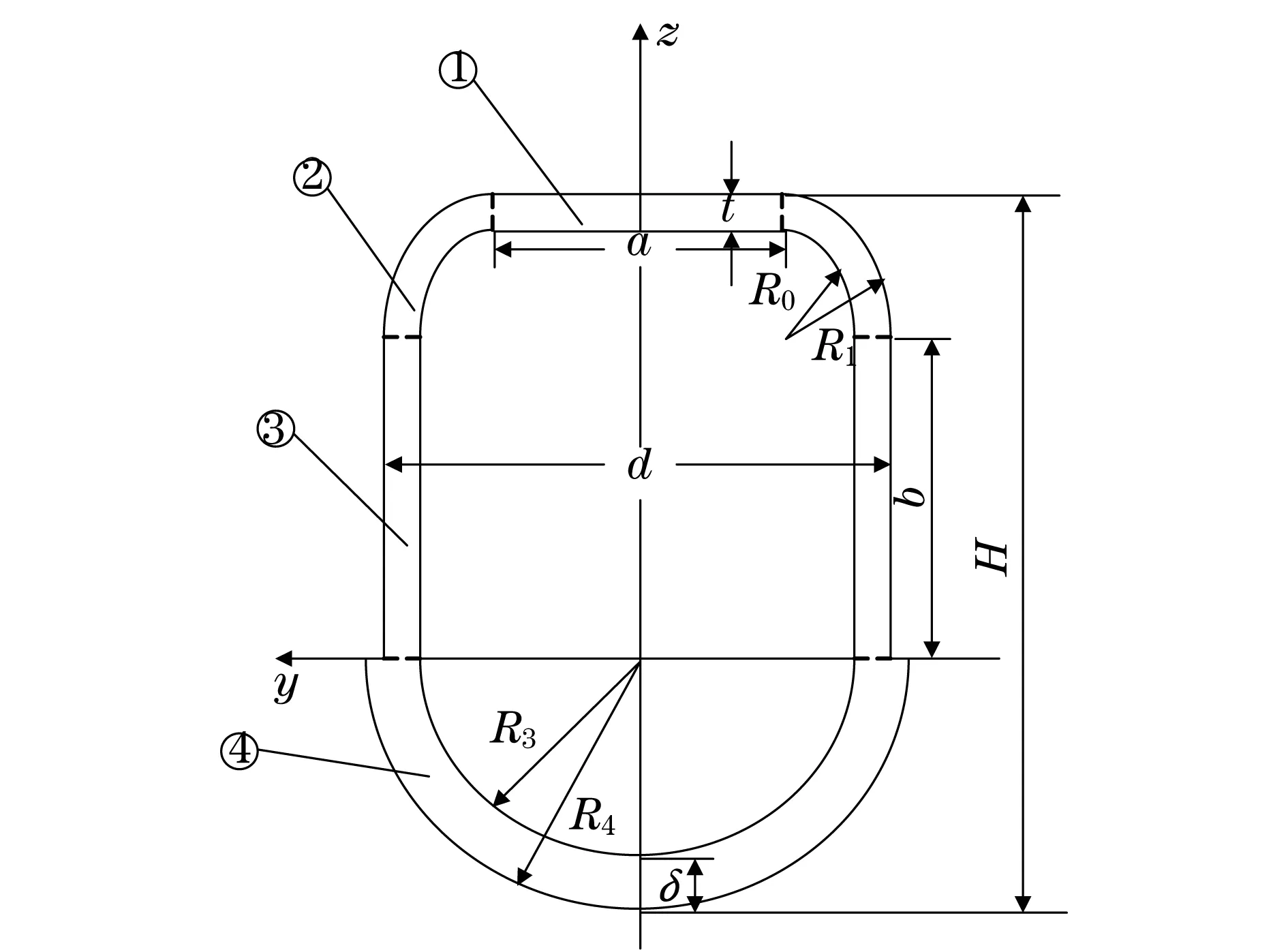
图1 U型截面Fig.1 U-section

根据惯性矩定理及U型截面的尺寸关系,计算可得,截面对z轴的惯性矩为

(5)

截面对y轴的惯性矩为

(6)

式中:t为上盖板厚度;a为上盖板矩形截面长度;R0为折弯内半径;R1为折弯外半径;b为腹板矩形截面的高度;d为截面宽度;δ为下盖板厚度.

2 U型截面各尺寸参数对截面惯性矩影响

本文详细分析了U型截面尺寸,包括折弯半径增量ΔR、上盖板厚度增量为Δt、下盖板厚度增量Δδ、截面宽度增量Δd、截面高度增量ΔH对截面惯性矩的影响.将各参数的变化量带入式(5)和式(6),得出各参数变化时z,y轴的惯性矩Iz,Iy.将U型截面的基本尺寸参数与各变化量数值带入,便可分析各尺寸参数变化时对截面惯性矩的影响.本文选取的U型截面尺寸参数以及变量数值,如表1所示,得到的相应惯性矩如图2～图6所示.

表1 U型截面基本尺寸参数以及各增量Tab.1 U-section basic dimensions and increments mm

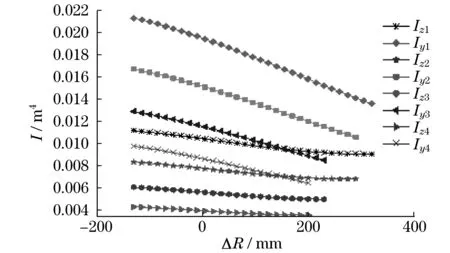
图2 截面惯性矩随折弯半径增量ΔR变化Fig.2 The inertia moment of the section changes with the bending radius increment ΔR

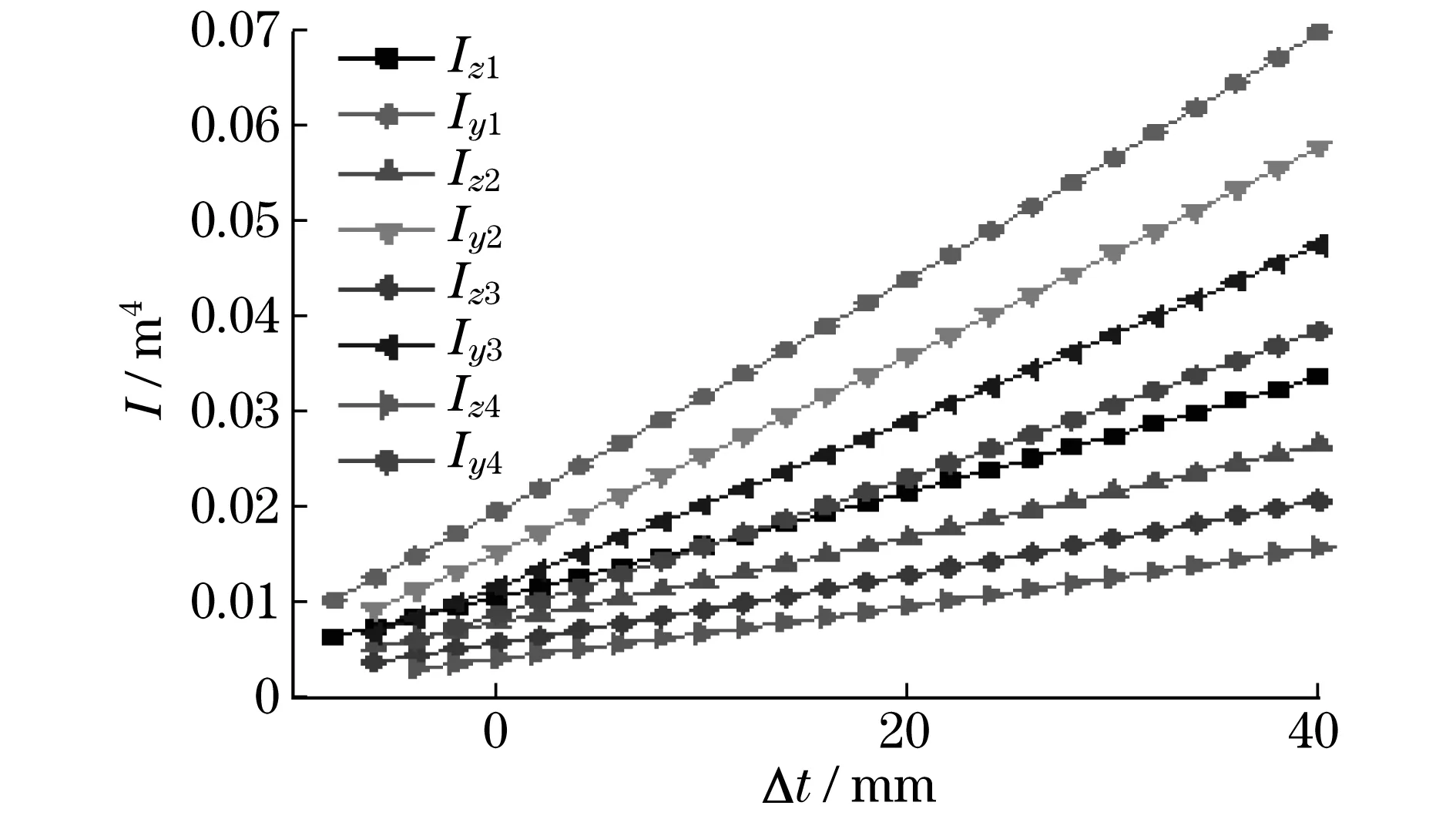
图3 截面惯性矩随上盖板厚度增量Δt变化Fig.3 The inertia moment of the section changes with the increment of the upper cover thickness Δt

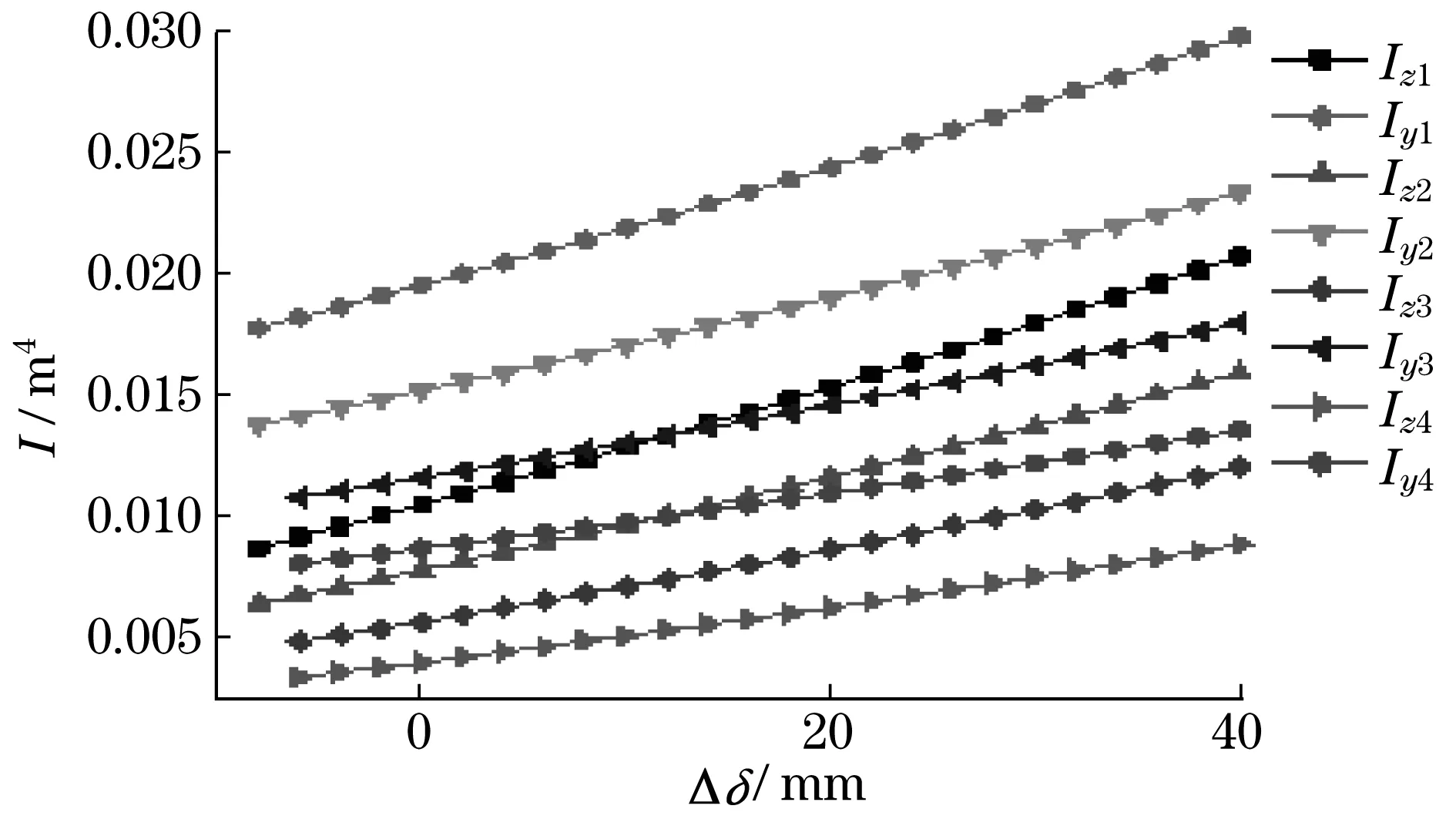
图4 截面惯性矩随下盖板厚度增量Δδ变化Fig.4 The inertia moment of the section changes with the increment of the lower cover thickness Δδ

从图2～图6可知,U型截面惯性矩随折弯半径(R0)增大而减小,随其余截面尺寸(H,d,t,δ)增大均增大.即意味着当U型截面的伸缩臂材料、支撑方式以及长度一定时,伸缩臂临界载荷随着R0增大而减小,随其余截面尺寸(H,d,t,δ)增大均增大.

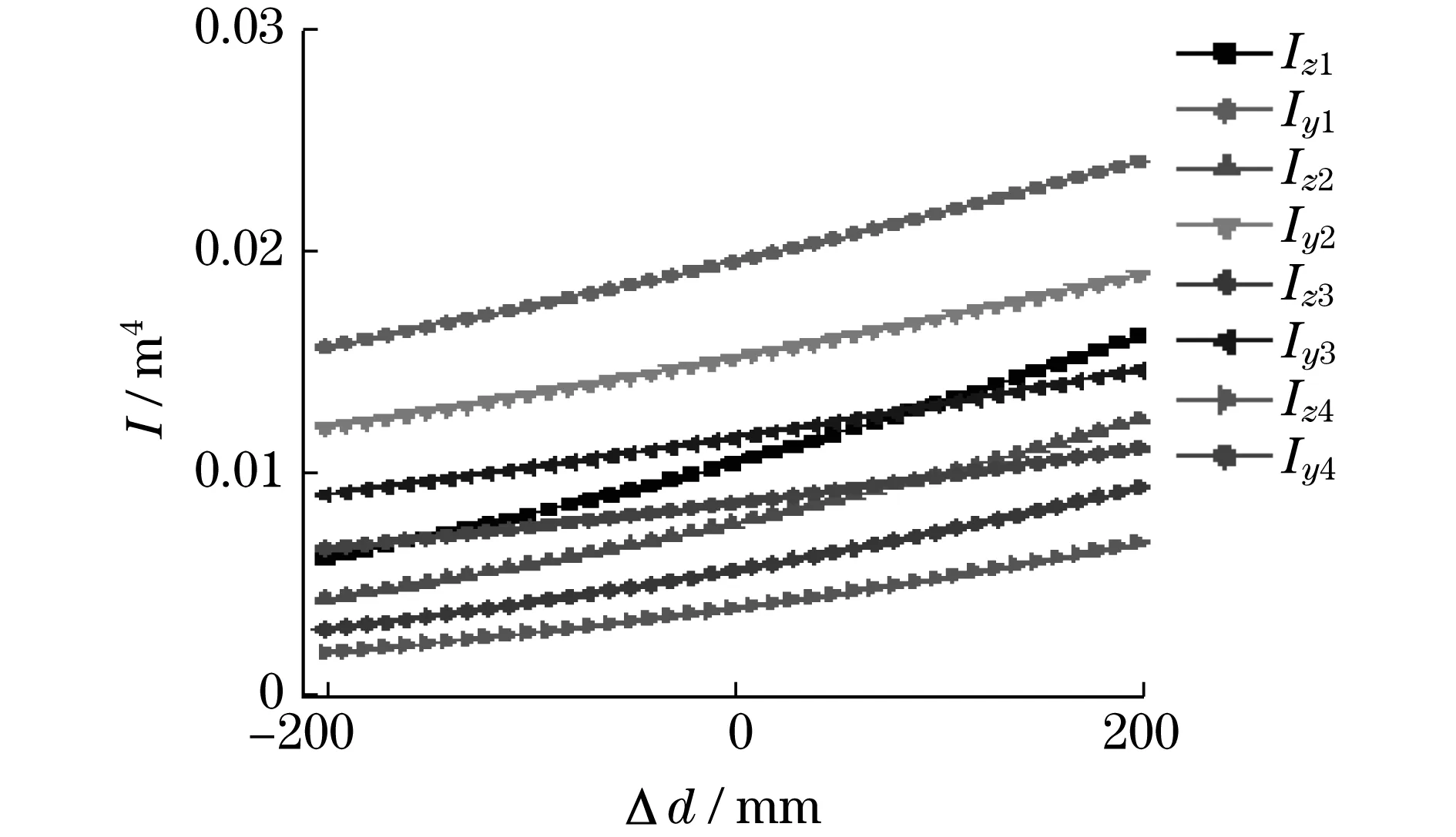
图5 截面惯性矩随截面宽度增量Δd变化Fig.5 The inertia moment of the section changes with the increment of the section width Δd

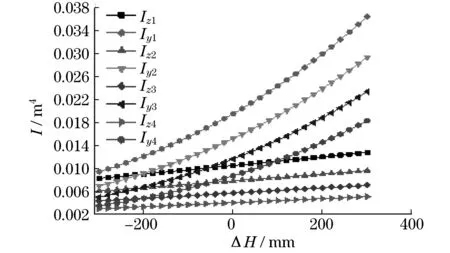
图6 截面惯性矩随截面高度增量ΔH变化Fig.6 The inertia moment of the section changes with the increment of thesection height ΔH

3 应用有限单元法分析截面尺寸对屈曲的影响

本文以某起重机厂生产的300 t全地面起重机伸缩臂为例,全伸长度61 m,变幅夹角76°,幅度14 m,额定起升吊载27.2 t.伸缩臂桶臂材料采用Weldox 1100,弹性模量为206 GPa,泊松比为0.3,屈服强度为1 100 MPa,抗拉强度为1 250 MPa.首先对伸缩臂进行有限元屈曲分析计算,然后利用Workbench中的Design Exploration模块进行线性屈曲敏感分析.在进行屈曲敏感分析时,选择基本臂所有截面尺寸(截面高度H0、截面宽度d0、折弯半径R0、上盖板厚度w01、下盖板厚度w02)以及其余截面厚度(w11,w12,w21,w22,w31,w32,w41,w42,w51,w52)作为设计变量,将屈曲载荷因子(Load Multiplier)作为输出变量.在ANSYS中线性屈曲临界载荷的计算等于初始载荷乘上屈曲载荷因子,当初始载荷不变时,屈曲载荷因子就直接表征了杆件抵抗屈曲的能力.屈曲敏感分析流程如图7,先进行静力学结构分析(Static Structural A);再进行线性屈曲分析(Linear Bucking B);最后进行Design Exploration中的相应面分析(Response Surface C).

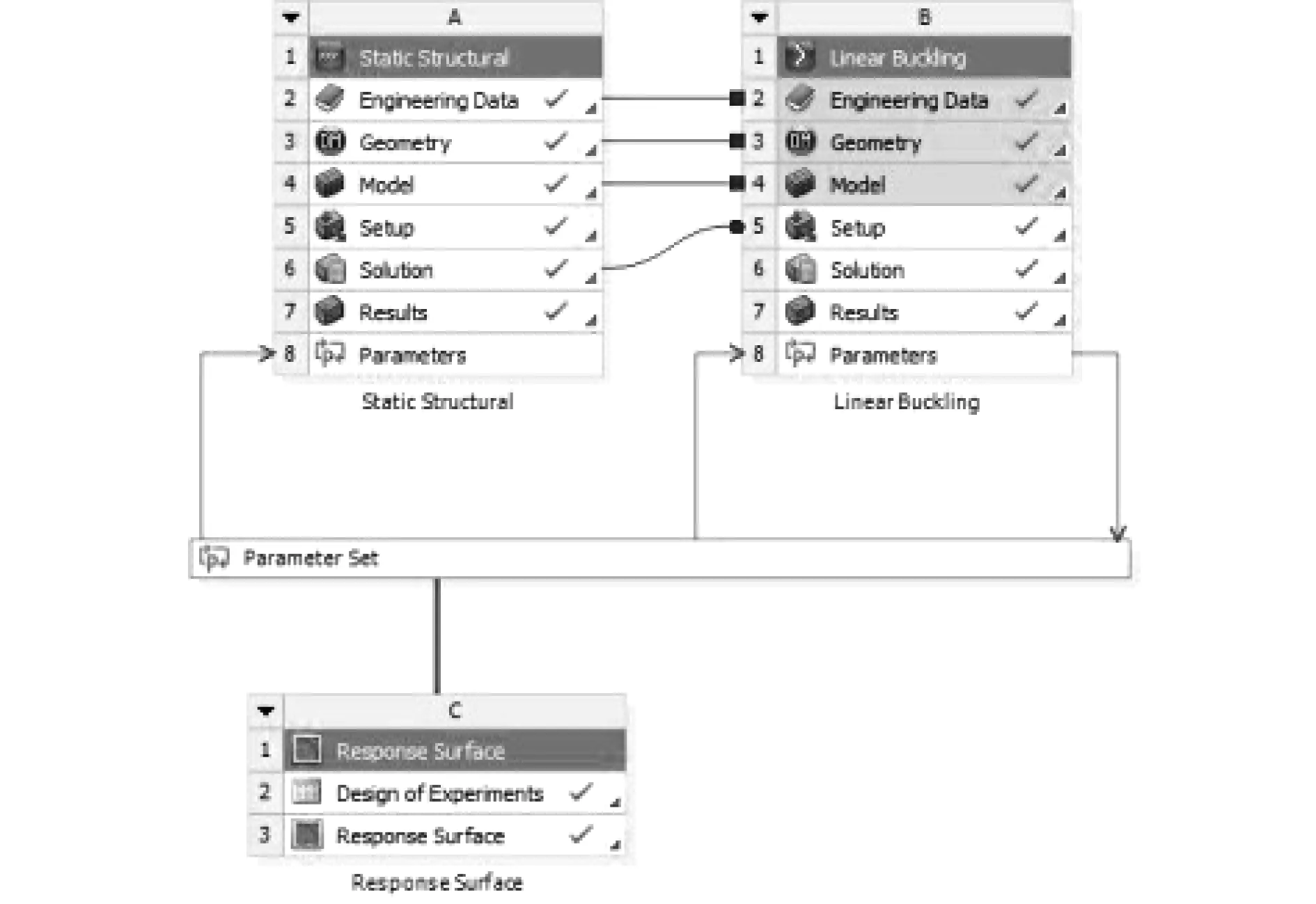
图7 屈曲敏感分析流程Fig.7 Flexion sensitive analysis process

3.1 有限元模型建立

Workbench中的Design Modeler模块提供了良好的建模功能.本文利用Design Modeler,采用概念建模方式，建立伸缩臂有限元模型.在草绘平面内先分别绘制6条与伸缩臂臂节等长的线段;然后利用Lines From Sketches形成线体,再为每条线体附上截面;最后将所有线体选中右键点击Form New Part,至此伸缩臂有限元模型建立完成,如图8所示.由于本文分析的是伸缩臂整体屈曲而非局部屈曲,故搭接滑块暂时不予考虑.

3.2 添加约束和载荷

为了模拟符合实际情况,将基本臂与转台的铰接点和变幅油缸与基本臂的铰接点处,分别添加Simply Supported,Fixed Rotation,将其沿x,y,z3个方向的平移自由度和绕y,z转动自由度约束,释放绕x轴转动自由度.伸缩臂受力众多,其中自重通过添加重力加速度g=9.8 m/s2考虑,钢丝绳拉力FS=55 151 N,起升载荷PQ=5.293 5×105N,臂头侧向水平力Ft+0.4PW=38 118 N(侧向水平力包括物品偏摆产生的水平力Ft和风载荷PW,物品偏摆角α=6°).

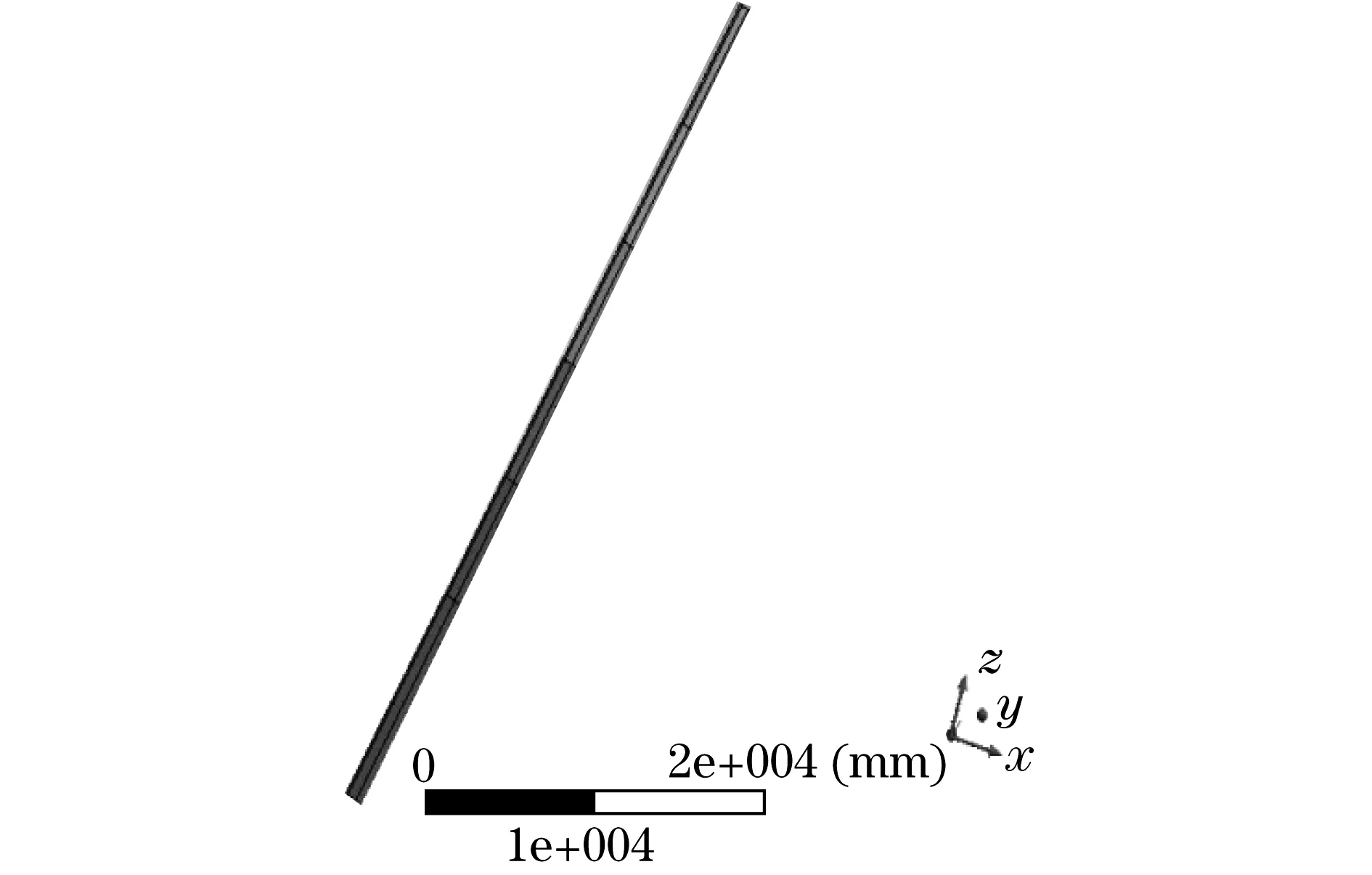
图8 伸缩臂有限元模型Fig.8 Finite element model of telescopic boom

3.3 划分网格

Workbench系统提供默认适应当前模型的方法,当线体采用默认的网格划分后,它的单元为BEAM188.为了细化网格可将Details of “Mesh”中的Relevance值设置为高点,本文设置为100,Relevance Center Fine设置为Fine.本文网格划分好后,Elements为103,Nodes为207.

3.4 求解及输出参数设置

当前处理工作完成后,分别单击Static Structural(A5)>Solution(A6)和Linear Bucking(B5)> Solution(B6)>Total Deformation.此时，可以求得当前载荷因子Load Multiplier为1.536 7,将其设置为输出参数.

3.5 建立Response Surface

双击Design Modeler模块中的Response Surface便可以建立响应曲面优化分析,它的优点是可以通过图表动态显示出输入与输出参数之间的关系以及敏感性等.双击Design of Experiments进行实验设计点的生成和计算,单击每一个输入参数可以对其上下界限进行设定,系统默认将输入参数的初始值(1±10%)作为上限和下限,单击Preview进行随机的实验点生成.本文采用系统默认方式,最终生成了288个设计点.设计点生成后,单击Update,便可以根据设计点的输入参数算出输出参数值.双击Response Surface(C)中的Response Surface项,单击Update进行更新.此时,便可以看到系统根据实验设计点进行了拟合后的图像.单击Response查看输入参数与输出参数的关系,如图9～图13所示(本文只给出了典型的输入参数和输出参数关系图).

由有限单元法得到的输入参数和输出参数关系可知，除屈曲载荷因子Load Multiplier随基本臂截面折弯半径(R0)增大而减小外,载荷因子随其他输入参数(H0,d0,w01,w02,w11,w12,w21,w22,w31,w32,w41,w42,w51,w52)增大均增大,这与之前对截面惯性矩的影响趋势完全一致.

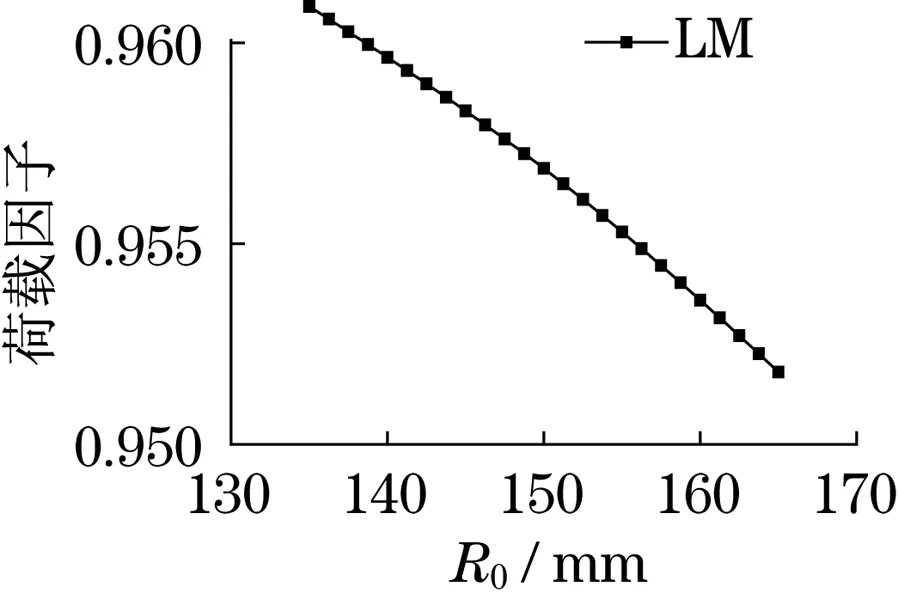
图9 折弯半径R0与载荷因子LM的关系Fig.9 Relationship between bending radius R0 and load factor LM

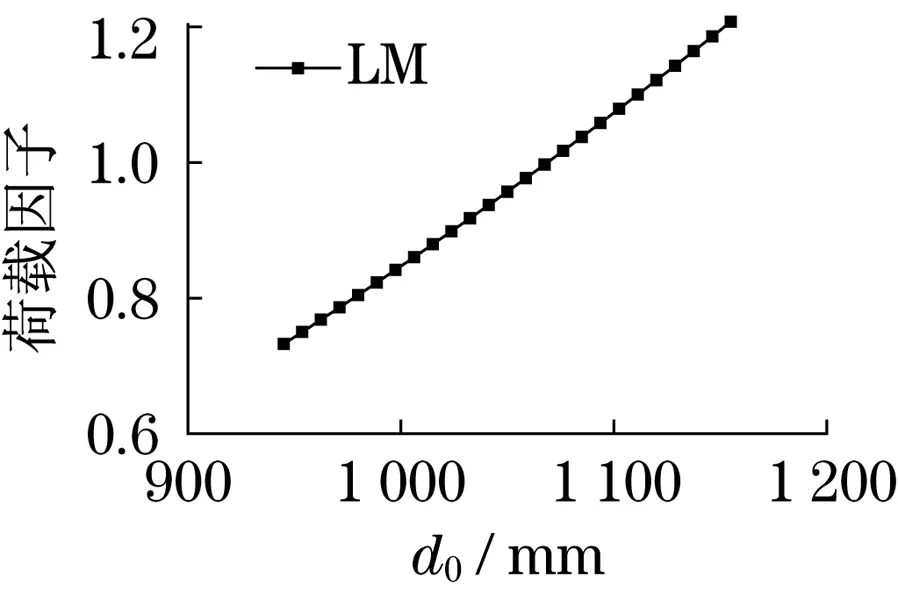
图10 截面宽度d0与载荷因子LM的关系Fig.10 Relationship between section width d0 and load factor LM

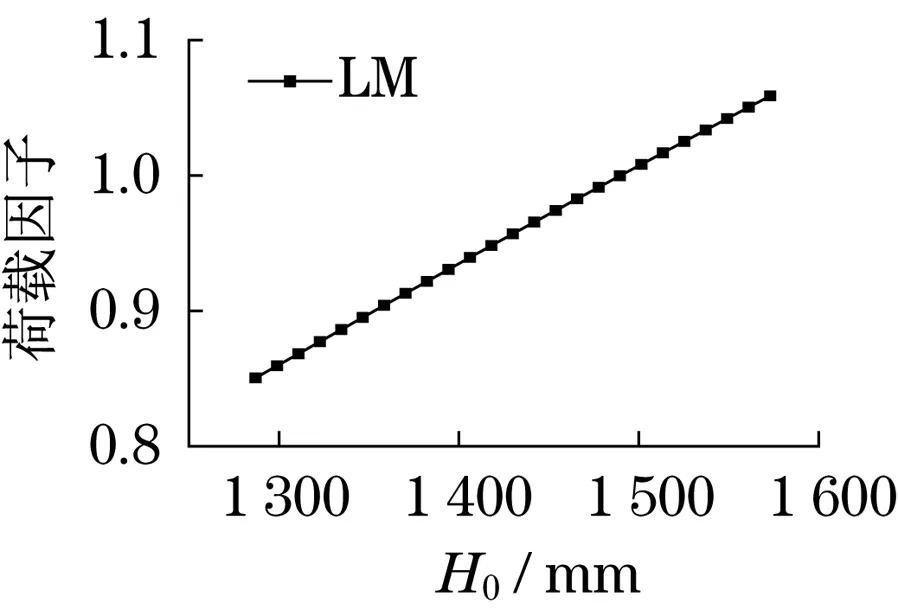
图11 截面高度H0与载荷因子LM的关系Fig.11 Relationship between section height H0 and load factor LM

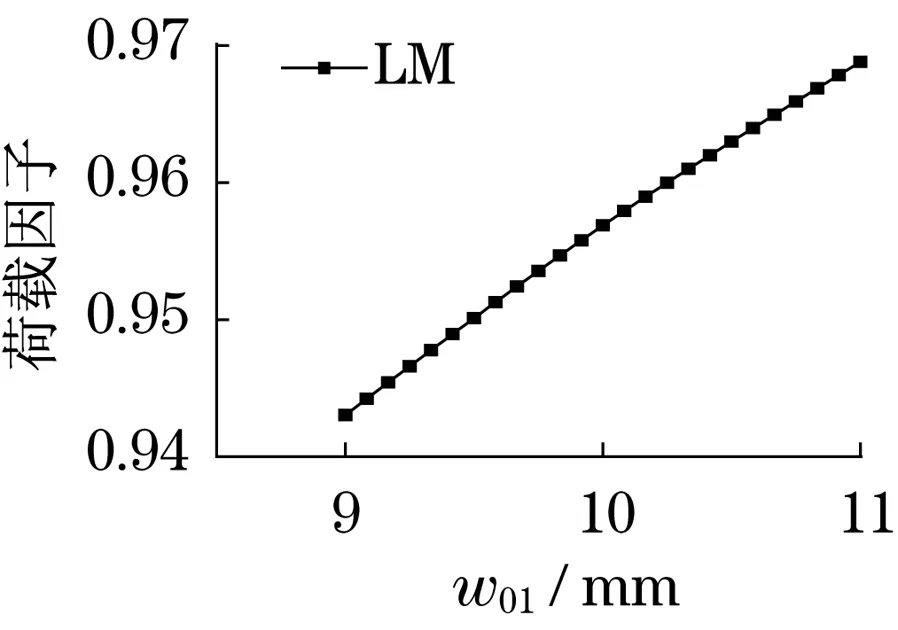
图12 基本臂上盖板厚度w01与载荷因子LM的关系Fig.12 Relationship between cover thickness w01 of basic boom and load factor LM

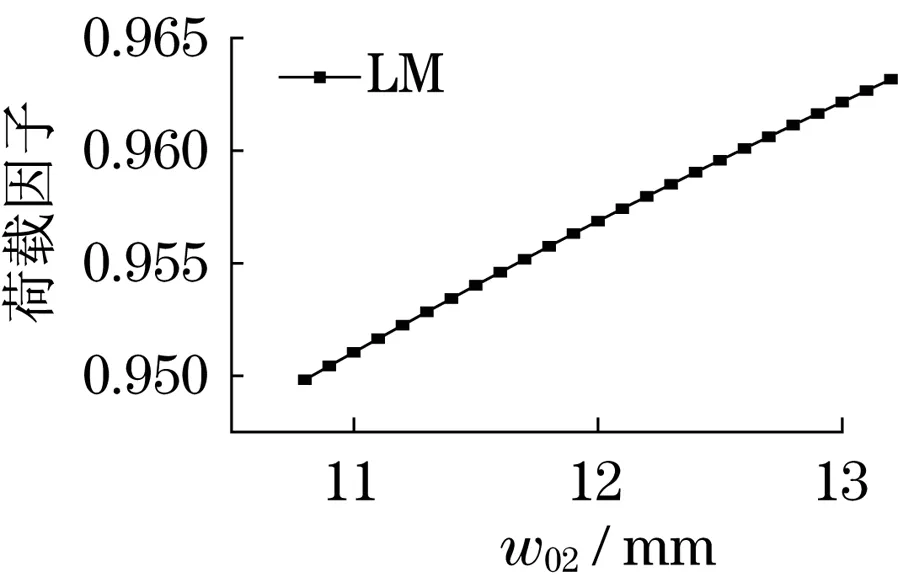
图13 基本臂下盖板厚度w02与载荷因子LM的关系Fig.13 Lower cover thickness w02 of basic boom and load factor LM

单击Local Sensitivity和Local Sensitivity Curves可以得到各输入参数对输出参数的敏感程度,在众多的输入参数中对屈曲载荷因子最为敏感的是基本臂截面宽度(d0),其次是基本臂截面高度(H0)，对载荷因子敏感性最小的是末节臂(臂头节)截面下盖板厚度(w52).

4 结论

本文通过分析U型截面参数对截面惯性矩的影响，采用有限单元法研究了截面尺寸对伸缩臂的屈曲临界力影响,彼此相互验证,发现当伸缩臂的材料、支撑方式以及长度一定时,伸缩臂屈曲临界力随着R0增大而减小,随其余截面尺寸(H，d，t，δ)增大均增大,对于其他截面可采用相同方法进行分析.通过敏感度分析可得知,对伸缩臂屈曲临界力最为敏感的是d0,其次是H0,敏感性最小的是末节臂(臂头节)w52.本文的研究分析结果可以给设计者提供一定的设计参考依据,以便采用合理的截面尺寸,提高伸缩臂的抗屈曲能力.