基于主成分分析的NBA球员综合能力评价

2018-09-04满帅龙华熊新李一民刘霖璇

软件导刊 2018年6期

满帅龙华熊新李一民刘霖璇

摘要：目前对球员综合能力的评价方法有TOPSIS法、灰色关联分析法等，但当评价指标量多时，存在计算效率低等缺陷，同时有些评价指标并不是值越大越好，且会对最优排序和最劣排序造成影响。为求取最适合的算法、作出准确的NBA球员综合能力评价，采用主成分分析法，以现役NBA联盟中538名运动员的得分、助攻、三分命中率等13项指标为实例，进行评价方法研究。分析球员多方面能力，得出球员在各项成分中得分排名并计算出各项能力最强的前十名球员，与体育界分析结果进行比较，分析球员的强项和弱项。实验结果表明，主成分分析能够高效地将数据降维，表现各项数据之间关联性，并且分析结果正确，适用于NBA球员综合能力评价。

关键词：主成分分析；NBA；球员综合能力评价

DOI：10.11907/rjdk.172838

中图分类号：TP391

文献标识码：A 文章编号：1672-7800（2018）006-0185-05

Abstract：At present， the evaluation methods of the player′s comprehensive ability mainly include Topsis method， gray correlation analysis and so on. However， the calculation efficiency is low when the evaluation index is large； indicator magnitude has an impact on optimal scheduling and worst ranking while not all large evaluation indicators equal better performance. Aiming to find the most suitable algorithm to make accurate evaluation of NBA players′ comprehensive ability， we use the principal component analysis to research the evaluation method with 13 indicators involving 538 NBA league athletes′ scores， assists， three point rates and other performance as examples. We analyze the players′ ability in various aspects， calculate the final scores， and select the top ten players to compare with the official analysis of NBA； and then we analyze the strengths and weaknesses of the players. The experimental results show that the principal component analysis can reduce the data dimensionality， present the relationship between the performance of the data and the results are correct.Therefore， it is applicable in NBA players' comprehensive ability evaluation.

Key Words：principal component analysis； NBA； evaluation of players′ comprehensive ability

0 引言

篮球作为一种主流运动，受到广大球迷（特别是大、中学生）的关注。NBA是世界男子篮球竞技水平最高的联赛，随着人民生活水平的提高，以及通信技术的飞速发展，中国对NBA联赛转播力度加大，我国人民对NBA的关注越来越多，在王治郅、姚明、易建联、周琦加入NBA后，由于其巨大的商业价值而受到了社会各界的关注。[1]

篮球运动员的综合能力评价一直是联盟、球队管理高层和球迷非常关心的事情。联盟每年都会颁发各种奖项，比如常规赛MVP、最佳新秀、进步最快球员、最佳防守球员等[2]，这也是对球员素质的评价。最终这些奖项归谁所有，仅仅根据球员一个赛季的上场表现，由美国资深体育评论员、体育记者、NBA技术官员和球迷投票选举产生是远远不够的[3]，因为这种评价中人为因素影响巨大，缺乏一套科学而严谨的评选体系，应该根据球员们的各项技术统计进行分析。现在NBA进入了大数据时代，NBA赛场采用SportVU技术[4]，通过使用6只摄像头追踪捕捉场上球员动作，每秒可记录25个动作，一场比赛可以收集到72 000个数据点，采集得到的原始数据积累成为海量数据库。利用这些海量原始数据，通常采用TOPSIS法、灰色关联分析法进行评价分析，但当评价指标量多时，计算效率低[5]，并且有些评价指标并不是值越大越好，对最优排序和最劣排序造成影响[6]，本文利用多元统计中的主成分分析法进行球员的综合能力分析，很好地解决了这个问题。

1 研究对象

本文选取NBA联盟中30只球队的所有运动员在2016-2017赛季的数据作为样本。选取球员上场时间、投篮命中率、三分命中率、罚球命中率、前场篮板、后场篮板、总籃板、助攻、抢断、盖帽、失误、犯规、得分，作为原始指标进行统计分析。

2 主成分分析法在NBA球员能力评价中的研究

2.1 TOPSIS法

TOPSIS法[7]即逼近理想解排序法，意为与理想方案相似性的顺序选优技术，是系统工程中有限方案多目标决策分析的常用方法。它是基于归一化后的原始数据矩阵，找出有限方案中最优方案和最劣方案（分别用最优向量和最劣向量表示），然后分别计算评价对象与最优方案和最劣方案的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。

但是利用TOPSIS法作NBA球员综合评价时，对高优指标和低优指标都很高的球员排名影响大，不能准确说明球员综合能力的高低[8]。

2.2 灰色关联分析法

灰色关联分析法[9]是一种通过灰色关联度分析和确定系统因素间的影响程度或因素对系统主行为贡献的测度方法。灰色关联分析的基本思想是根据序列曲线几何形状的相似程度判断其联系是否紧密。

但是利用灰色关联分析法作NBA球员综合评价时，存在分辨系数取值问题，并且球员的某些最优指标并不是越大越好，比如失误和犯规，利用该方法对球员的综合能力作评价存在误差[10]。

2.3 主成分分析法基本概念及原理

主成分分析法（Principal Component Analysis）[11]是一种通过“降维”的思想将多个指标的数学统计量转化为少数有代表性的指标量的数学统计方法，采用降维的思想解决高维度系统的寻优问题[12]。其基本原理是：通过一个正交变换把问题中本来相互关联的随机变量转换为一些不相关的新变量。数学上来说，这种方法是将变量的协方差矩阵转化为相应的对角矩阵，将原来的变量系统通过正交变换，构成一个新的正交系统[13]，使原本相关的样本点散列成正交方向，成为不相关的正交变量。

2.4 算法步骤

X-dp表示第d个球员的第p个技术统计参数，其中p=（1，2…13），分别代表球员的场均上场时间、投篮命中率、三分球命中率、罚球命中率、场均前场篮板个数、场均后场篮板个数、场均总篮板个数、场均助攻数、场均抢断个数、场均盖帽数、场均失误数、场均犯规个数以及场均得分。

在评价过程中，因为X-dp是有量綱的变量，容易对评价结果产生不必要影响，因此，根据主成分分析法对样本进行评价，需要对样本按照公式（4）进行无量纲化处理[14]。其中，定义x-d′p′是无量纲化后的样本值，X-dp是样本值，X-p为样本均值，见公式（2）：

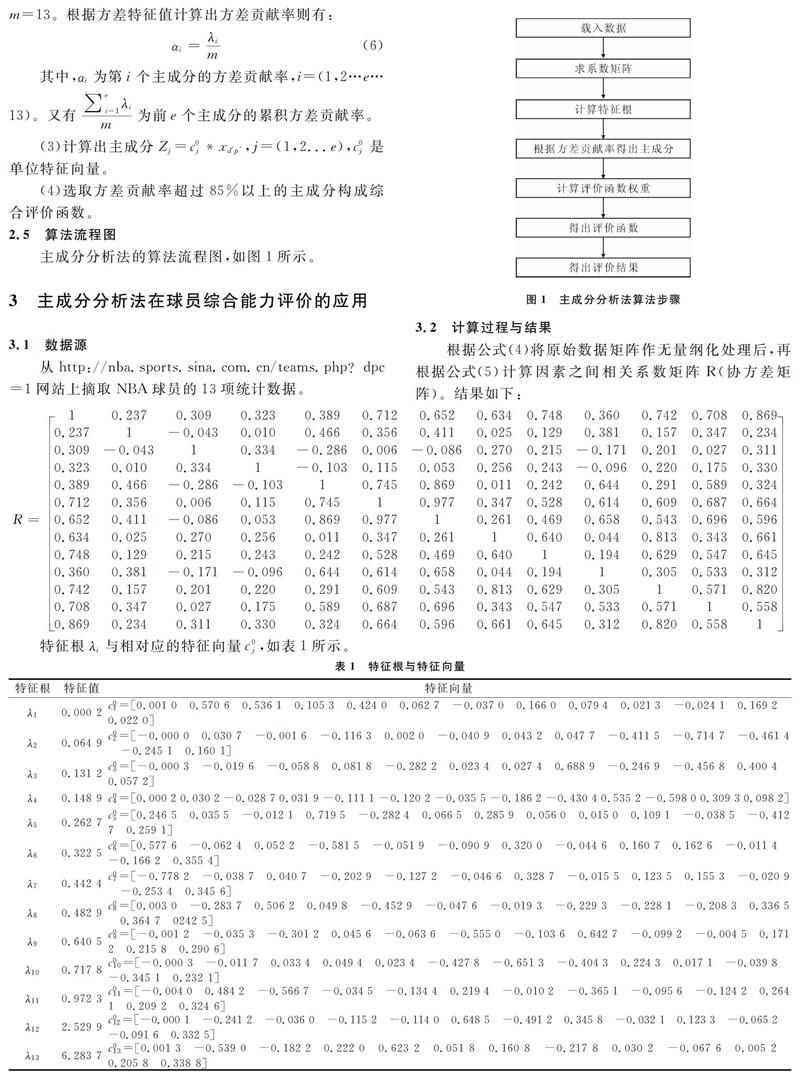
2.5 算法流程图

主成分分析法的算法流程图，如图1所示。

3 主成分分析法在球员综合能力评价的应用

3.1 数据源

从http：//nba.sports.sina.com.cn/teams.php？dpc=1网站上摘取NBA球员的13项统计数据。

3.2 计算过程与结果

根据公式（4）将原始数据矩阵作无量纲化处理后，再根据公式（5）计算因素之间相关系数矩阵R（协方差矩阵）。结果如下：

特征根λ-i与相对应的特征向量c0-j，如表1所示。

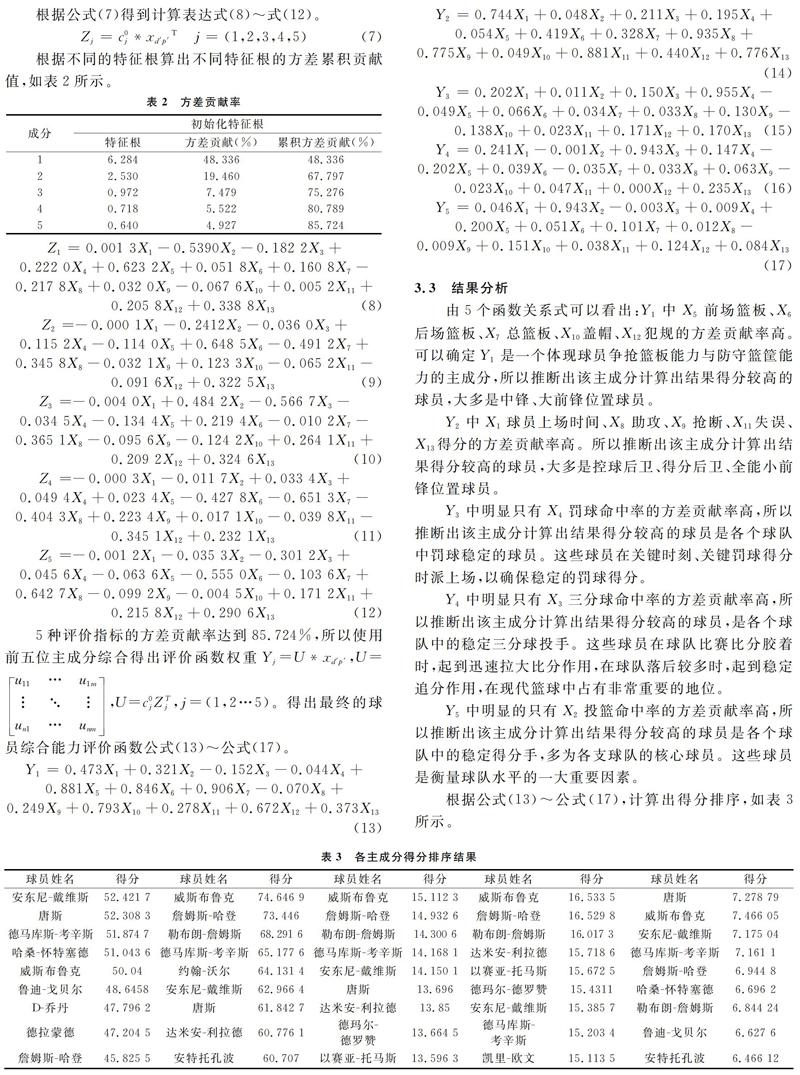
根据不同的特征根算出不同特征根的方差累积贡献值，如表2所示。

3.3 结果分析

由5个函数关系式可以看出：Y-1中X-5前场篮板、X-6后场篮板、X-7总篮板、X-10盖帽、X-12犯规的方差贡献率高。可以确定Y-1是一个体现球员争抢篮板能力与防守篮筐能力的主成分，所以推断出该主成分计算出结果得分较高的球员，大多是中锋、大前锋位置球员。

Y-2中X-1球员上场时间、X-8助攻、X-9抢断、X-11失误、X-13得分的方差贡献率高。所以推断出该主成分计算出结果得分较高的球员，大多是控球后卫、得分后卫、全能小前锋位置球员。

Y-3中明显只有X-4罚球命中率的方差贡献率高，所以推断出该主成分计算出结果得分较高的球员是各个球队中罚球稳定的球员。这些球员在关键时刻、关键罚球得分时派上场，以确保稳定的罚球得分。

Y-4中明显只有X-3三分球命中率的方差贡献率高，所以推断出该主成分计算出结果得分较高的球员，是各个球队中的稳定三分球投手。这些球员在球队比赛比分胶着时，起到迅速拉大比分作用，在球队落后较多时，起到稳定追分作用，在现代篮球中占有非常重要的地位。

Y-5中明显的只有X-2投篮命中率的方差贡献率高，所以推断出该主成分计算出结果得分较高的球员是各个球队中的稳定得分手，多为各支球队的核心球员。这些球员是衡量球队水平的一大重要因素。

根据公式（13）～公式（17），计算出得分排序，如表3所示。

结合上表，可以得出以下结论：

（1）Y-1得分主要与前场篮板、后场篮板、总篮板、盖帽和犯规有强正相关，得分的高低表示球员的拼抢篮板能力强防守效率。根据上表中的数据可以看出：安东尼·戴维斯、卡尔·安东尼·唐斯、德马库斯·考辛斯、哈桑·怀特塞德、威斯布鲁克、戈贝尔、小乔丹、德拉蒙德和詹姆斯·哈登的得分在全联盟538名球员中排名前十，说明这些球员在拼抢篮板能力强、防守效率较高，这也与实际能力情况相符。安东尼·戴维斯、卡尔·安东尼·唐斯、德马库斯·考辛斯是当今NBA联盟中公认的内线基石球员，他们在场上的位置都为内线球员，可以扛起球队的后场篮板球保护、前场篮板球拼抢以及守护篮筐，不让对手轻易得分。

（2）Y-2得分主要与助攻、抢断、失误以及得分贡献率有关，得分高低表示球员的带动球队攻防能力和个人得分能力。根据上表中的数据可以看出：威斯布鲁克、詹姆斯·哈登、勒布朗·詹姆斯、德马库斯·考辛斯、约翰·沃尔、安东尼·戴维斯、卡尔·安东尼·唐斯、达米安·利拉德和安特托孔波的得分在全联盟538名球员中排名前十，说明这些球员在带队攻防能力和个人得分能力出众，与实际情况相符。威斯布鲁克、詹姆斯·哈登、勒布朗·詹姆斯是当今NBA联盟中带队能力最好的三位球员，他们在场上的位置为后卫和小前锋，均为外线球员，能够在场上创造机会，精准把球传给队友，关键时刻还可以依靠超强的个人能力得分。这10个人中除了德马库斯·考辛斯、安东尼·戴维斯和卡尔·安东尼·唐斯是内线球员，其他均为外线球员，证明了Y-2得分较高的球员，大多是控球后卫、得分后卫、全能小前锋位置球员的推断。内线球员能上该排名的前十，说明他们不仅有强壮的身体、细腻的手感，还有后卫般控球能力和传球意识。这也是德马库斯·考辛斯、安东尼·戴维斯和卡尔·安东尼·唐斯成为NBA联盟中最好的内线基石球员的有利证据。

（3）Y-3得分主要与罚球命中率的贡献率有关，得分高低表示球员的罚球稳定性和持球进攻杀伤的能力。根据上表中的数据可以看出：威斯布鲁克、詹姆斯·哈登、勒布朗·詹姆斯、德马库斯·考辛斯、安东尼·戴维斯、卡尔·安东尼·唐斯、达米安·利拉德、德玛尔·德罗赞、以赛亚·托马斯和保罗·乔治的得分在全联盟538名球员中排名前十，说明这些球员的罚球稳定性和持球进攻造杀伤能力很强，与实际情况相符。这些球员都是球队中核心球员，比赛中是执行关键罚球和关键时刻持球个人进攻的最好人选。

（4）Y-4得分主要与三分命中率的贡献率有关，得分高低表示球员的三分稳定性和迅速得分能力。根据表3中的数据可以看出：威斯布鲁克、詹姆斯·哈登、勒布朗·詹姆斯、达米安·利拉德、以赛亚·托马斯、德玛尔·德罗赞、安东尼·戴维斯、德马库斯·考辛斯、凯里·欧文和约翰·沃尔的得分在全联盟538名球员中排名前十，说明这些球员三分命中率很稳定，除了德玛尔·德罗赞（三分命中率26.6%）和安东尼·戴维斯（三分命中率29.9%）受得分因素影响较大、排名进入前十以外，其他人均于实际情况相符。

（5）Y-5得分主要与投篮命中率的贡献率有关，得分高低表示球员的投篮稳定性。根据表3中的数据可以看出：卡尔·安东尼·唐斯、威斯布鲁克、安东尼·戴维斯、德马库斯·考辛斯、詹姆斯·哈登、哈桑·怀特塞德、勒布朗·詹姆斯、鲁迪·戈贝尔、安特托孔波和的德安德烈·乔丹的得分在全联盟538名球员中排名前十，说明这些球员的投篮命中率稳定，是球队中的稳定得分手，与实际情况符合。而且这些球员除了威斯布鲁克、詹姆斯·哈登、勒布朗·詹姆斯，其他均为内线球员，实际比赛中内线球员的得分范围较接近篮筐，所以命中率较高，验证计算准确。

基于主成分分析结果，可以得出基于5个主成分的得分靠后的运动员应该对自己薄弱的环节进行补强。以达米安·利拉德和安托特孔波为例，达米安·利拉德从数据上和实际能力上都已经达到了全明星水准，可是这几年却频频入选不了全明星，这不排除球迷的主观喜爱程度和对其能力的评价标准，但是基于本文中的数据分析评价，达米安·利拉德在Y-1的得分排名是第29名，在Y-2的得分排名是第8名，在Y-3的得分排名是第7名，在Y-4的得分排名是第4名，在Y-5的得分排名是22名。很显然他需要提高的是Y-1和Y-5上体现出的能力，即提升篮板球拼抢能力和投篮命中率。但是实际情况是，达米安·利拉德是后卫位置球员，身材相对矮小，很难提高篮板球拼抢能力，而且将后卫和内线高大球员在抢篮板球的上作比较也是不合理的，所以他切实需要加强的是在场上减少犯规数和通过训练提高投篮命中率，这样才能有目的地训练自己，提升为全明星球员。安托特孔波拥有极强的身體天赋，身材高大但不缺灵活性，四肢奇长，有出色的运动能力，被业界评论是可以超越杜兰特的球员，但是要真正超越杜兰特，安托特孔波还需要提高一些方面的能力。安托特孔波在Y-1的得分排名是第11名，在Y-2的得分排名是第9名，在Y-3的得分排名是第15名，在Y-4上的排名是第22名，在Y-5的得分排名是第9名。可以明显得出安托特孔波需要提高在Y-3和Y-4上的能力，即三分球命中率和罚球命中率。在实际情况中，安特托孔波的罚球命中率为77%，三分球命中率为27.2%，预期比较的杜兰特罚球命中率为87.5%，三分球命中率为37.5%，两者差距较大。所以安托特孔波需要努力提升罚球命中率和三分球命中率，才能成为像杜兰特一样的超级得分手。

4 结语

在利用主成分分析法进行NBA球员综合能力评价的过程中，算法在应用中表现出一些优势：首先，可以在保证变量数据信息损失很小的情况下，实现从高维空间到低维空间的转化。在有538组原始数据的情况下，通过主成分分析法降维，使变量之间的分析更为容易。其次，主成分分析法选取正交化的综合评价指标作为主成分，规避了球员综合能力评价指标间的不确定关系，因为提取的综合变量之间相互正交，所以消除了原始变量之间的多重相关性。综上所述，主成分分析法在篮球运动员的综合能力评价中具有良好的适用性。

参考文献：

[1] 郭兆辉.NBA智能系统的启示[J].软件和信息服务，2012（07）：45.

[2] 王彦霞，齐秀英.运用TOPSIS法和综合指数法综合评价医院医疗工作质量[J].中国病案，2015，16（10）：21-23.

[3] 王平，王云峰.综合权重的灰色关联分析法在河流水质评价中的应用[J].水资源保护，2013，29（05）：52-54+64.

[4] 何思长，赵大仁，孙渤星，刘志会，张瑞华.基于TOPSIS法和RSR法模糊联合的医疗联合体实效评价[J].中国医院管理，2016，36（05）：7-9.

[5] 顾洲一，邱瑾.基于熵权TOPSIS评价法的NBA教练执教水平评价模型研究[J].南京体育学院学报（自然科学版），2015，14（05）：152-157.

[6] 黄寰，王玮.基于改进灰色关联分析法的工业园区循环经济评价研究[J].软科学，2016，30（06）：130-133+144.

[7] 董伦红.我国男篮优秀大前锋若干特征分析与评价[J].广州体育学院学报，2005（04）：76-78.

[8] 苏为华.我国多指标综合评价技术与应用研究的回顾与认识[J].统计研究，2012，29（08）：98-107.

[9] 曹伟.基于改进型PSO-BP神经网络算法的水环境质量评价[D].昆明理工大学，2016.

[1] 吴翔峰.14-16年NBA优秀控球后卫与得分后卫攻防能力的对比分析[D].北京：北京体育大学，2017.

[2] 王晓明.2015-2016赛季NBA季后赛各队攻、防能力比较研究[D].济南：山东师范大学，2017.