基于奇异值分解理论的柔性高压直流输电线路双端故障测距组合算法

刘小磊 李冰心 赵峰

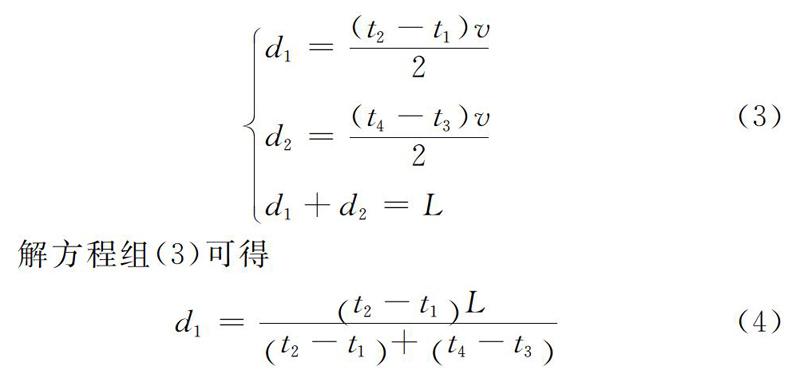
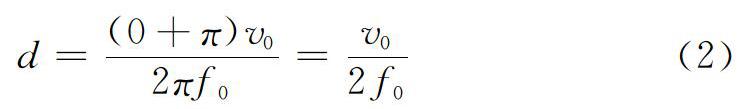
摘 要：柔性高压直流输电系统大多采用地下电缆作为输电线路，由于地下电缆行波波头衰减严重，导致在长距离故障测距时很难准确测出故障点反射波到达测量点的时刻。为了实现精确的故障测距，将奇异值（SVD）分解算法应用到固有频率法与行波法相结合的组合算法中。首先利用故障行波的固有频率计算出故障点的大概位置，算出故障点反射波分别到达两端母线的时间范围，然后对故障行波信号进行奇异值分解，得到SVD第二分量奇异值检测结果，依据固有频率法算出的时间范围确定反射波头到达两端母线的准确时刻。最后将初始行波和故障点反射波分别到达两端母线的时间代入消除波速影响双端测距公式，计算出故障点的准确位置。PSCAD和MATLAB仿真证明该方法测距精度较高。

关键词：柔性高压直流；行波法；固有频率；奇异值分解；双端故障测距；波速

DOI：10.11907/rjdk.172745

中图分类号：TP319

文献标识码：A 文章编号：1672-7800（2018）006-0173-05

Abstract：In most cases underground cables are utilized as the transmission lines in flexible high voltage direct current transmission （VSC-HVDC） system， but the serious attenuation of the underground cable wave head leads to great difficulties in accurately measuring the arrival time of fault point reflected waves. Therefore a new algorithm of two terminal fault location combining natural frequency and traveling wave method based on the time-frequency characteristics of fault traveling wave is proposed. Firstly， the natural frequency of the fault traveling wave is used to calculate the approximate location of the fault point， so that the time range of the reflected wave between the bus at both ends can be calculated. Then the singular values of the fault traveling wave are decomposed， and the singular points of the fault signals are detected by the pulse of second SVD components， according to the corresponding time range； the accurate time of the wave head reaching the bus at both ends is determined. VSC-HVDC transmission lines are on on both sides of the combined capacitor， so the fault traveling wave in the bus has total reflection. At the same time， we put forward a algorithm eliminating the influence of wave velocity of two terminal fault location by the initial traveling wave and time equations that reflect when wave reaches the fault point respectively at both ends of bus time equations are listed， and then calculate the distance and determine the exact location of the fault point. PSCAD and MATLAB simulations show that the proposed algorithm has higher ranging accuracy and can solve the problem of the recognition of the reflected wave head.

Key Words：flexible high voltage direct current； traveling wave method； natural frequency； SVD； two terminal fault location； wave velocity

0 引言

柔性高壓直流输电VSC-HVDC（voltage source converter-high voltage direct current transmission）是一种以电压源换流器和脉宽调制等技术为基础的新一代直流输电技术，具有较好的可控性和灵活性，在新能源发电并网、孤岛供电等领域有很好的应用前景[1]。直流输电线路大多距离较长，故障发生率较高，且故障发生后故障点的查找比较困难。因此，研究精确可靠的故障测距技术，对于保证电力系统安全运行，提高系统可靠性和经济性有着极为重要的作用。直流故障测距装置主要采用行波法进行测距，行波测距法响应速度快、测距精度高，理论上不受过渡电阻、故障类型和相角等因素影响[2-6]。行波测距分为单端测距法和双端测距法[7]。单端测距法是指根据故障初始行波从故障点到测量点往返一次所用的时间和波速计算故障点位置；双端测距法是指利用故障初始行波分别到达两端测量点的时间差和波速计算故障点位置。

行波法测距需要对故障点反射波头进行准确识别，这就降低了测距的可靠性[8-9]。而基于固有频率的测距算法则不受波头识别困难的影响，只需在任意故障暂态数据提取固有频率就能进行测距。该算法测距的精度明显低于行波法，但可靠性较高、稳定性强，可以对故障点位置进行粗略估算。本文将奇异值（SVD）分解算法用到固有频率法与行波法相结合的组合算法中，利用两种测距方法优势互补[10-11]，将奇异值分解（SVD）算法引入使得测距计算更为精确。该算法首先利用固有频率法测出故障点的粗略值，计算出故障点反射波到达两端测量点的时间范围，从而实现对反射波头精确时刻的主动识别，很大程度上提高了测距的可靠性，而奇异值（SVD）分解具有准确识别故障信号的优点，能得到更为精确的时间参数。经过PSCAD仿真和MATLAB数据处理，证明该测距算法能实现高压直流输电线路可靠、精确的故障测距。

1 固有频率法测距

输电线路发生故障时，形成故障暂态行波，在频域上表现为一系列特定频率谐波的形式，称为固有频率，固有频率值与故障距离呈函数关系。文献[12]研究了故障行波频率、边界条件和故障距离之间的关系：

输电线路发生金属性接地短路时，故障行波在短路点的反射系数为-1，也就是说α-F为π；直流输电线路母线处装有平波电抗器，一般情况下故障暂态行波频率较高，平波电抗器阻抗较大，可以近似认为是开路，反射系数为1， α-F取π。在故障行波的频谱中，第一个峰值对应的频率最大，为主频，利用主频对故障点进行测距最为简单易行，这时对应的测距公式为：

固有频率法测距是根据故障行波的固有频率进行测距的，不用识别故障点反射波头。用向后预测的prony算法提取故障电流行波的固有频率。故障行波波头平缓，在时域范围内对行波波头的标定比较困难。但是经过时频转变后，可以有效提取固有频率值，实现故障测距。该方法抗高阻能力强，受噪声干扰小，可靠性高，缺点是测距精度不高。

2 双端故障测距算法

行波在线路中传播时，在母线、故障点和线路中的不连续点处都会发生反射和折射，而对于VSC-HVDC而言，系统两端并联有大电容，行波会在母线处发生全反射。传统双端测距法只是根据行波到达两端母线的时间差进行故障定位，完全没有考虑波速不确定性对测距精度带来的影响。行波在不同的电压等级和线路状态以及线路参数下传播速度是不同的，一般情况下，波速的取值范围是0.936c（11kV）～0.987c（500kV），这给测距带来了较大误差。在传统行波法测距的基础上，利用故障初始行波，将故障点的反射波分别到达测量点的时间参数和波速、故障距离的关系列出方程组，求解得到测距公式，这种算法能够消除波速影响[13]。

VSC-HVDC输电线路发生接地短路的故障最多，本文对此进行研究。图1为输电线路模型，线路在F点处发生接地短路，M端为整流侧，N端为逆变侧。由于VSC-HVDC输电线路两端并联大电容，所以故障行波在母线M、N处发生全反射。

故障行波传输网络如图2所示，t-1为故障初始行波到达M端测量点的时间，t-2为故障行波经M端母线和故障点反射后再次到达M端测量点的时间，t-3为故障初始行波到达N端测量点的时间，t-4为故障行波经N端母线和故障点反射后再次到达N端测量点的时间。

设MN之间的长度为L，故障点F到M端、N端母线的距离分别为d-1和d-2，波速为v。可列出式（3）：

測距公式（4）是关于时间和距离的式子，消除了波速不确定给测距带来较大误差的影响，而t-1、t-2、t-3、t-4的测量不需要时间同步，消除了时间不同步带来的误差，因此不需要GPS双侧时钟同步，节约了测距装置成本。若两端故障点反射波没有检测到，就只能用传统双端测距进行故障定位。

3 SVD分解与奇异性检测

4 双端故障测距组合算法

综上所述，固有频率法是在频域上对故障点进行测距，行波法是在时域上对故障点进行测距，行波法测距精度高，固有频率法可靠性好，两种测距方法可以优势互补。本文在行波法和固有频率法结合的基础上[10-11]，用奇异值分解（SVD）算法对故障行波信号进行处理，得到的测距结果更为精确。

4.1 固有频率法初测

设利用固有频率法初步测量得到的故障距离为x，大量仿真实验表明，在任何形式的故障下，利用固有频率法测距得到的结果误差最大不超过10%，则实际故障距离范围为（0.9x，1.1x），代入传统测距公式d=v（t-2-t-1）2，可以算出故障点反射波到达M端母线的时间t-2的范围为t-1+1.8xv，t-1+2.2xv。同理，可得到t-4的范围为t-3+1.8（L-x）v，t-3+2.2（L-x）v。

4.2 波头识别

故障行波会在线路上阻抗不连续点处发生突变，对故障电压行波信号进行奇异值分解，利用SVD第二分量脉冲极大值或极小值确定故障初始行波和故障点反射波分别到达两端测量点的位置。

4.3 双端测距

首先根据SVD第二分量脉冲的极值确定故障初始行波分别到达两端测量点的时刻t-1和t-3，然后用固有频率法算出故障点反射波到达两端母线的时间范围，识别出故障点反射波经SVD第二分量分解后对应的准确时刻t-2和t-4，将t-1、t-2、t-3、t-4带入公式（5）计算出故障点的确切位置。

5 仿真验证

为了验证本文故障测距新方法的定位精度，在PSCAD中搭建如图3所示的VSC-HVDC模型，额定电压为±110kV，容量为75MW，线路长度为200km，采样频率为1MHz，两端分别并联 1000μF的大电容，采用PSCAD对输电系统进行仿真，并用MATLAB进行数据处理。

设置在距离M端20km处发生接地短路故障，过度电阻为100Ω时，经PSCAD仿真后得到的M和N端的故障电压波形如图4所示。

首先用向后预测的Prony算法提取故障行波的固有频率，其中主频f-0=7 326Hz，在电压等级为110kV下v-0取0.936c，代入公式（3）得x=19.165km，从而得出t-2的范围为（t-1+122.853，t-1+150.153），同理可求出t-4的范围为（t-3+1159.199，t-3+1416.798）。对故障电压行波进行奇异值分解，得到SVD第二分量奇异值检测结果如图5、图6所示。根据SVD检测结果提取突变点极值，可以看出，利用SVD分解到的第二分量信号能够准确测出故障初始行波到达母线的时刻t-1和t-3，t-1=70μs，t-2=204μs。算出t-3和t-4范围，从而确定其对应的突变点精确时刻： t-3=605μs，t-4=1809μs，代入公式（4）得d-1=20.029 9km，误差为0.029 9km，可知测距精度较高。

在不同故障距离和过度电阻下的测距结果如表1所示。

用传统测距方法对故障点进行计算，与新方法对比，测距结果如表2所示。

从表1、表2测距结果可以看出，新测距方法的测距结果比传统测距方法的测距误差要小很多，而且消除了波速影响，具有波头识别优势，测距精度更高。

6 结语

本文基于VSC-HVDC线路故障测距的可靠性和精确性，将奇异值（SVD）分解算法用到固有频率法与行波法相结合的组合算法中。行波法和固有频率法各有优点，将两种测距方法优势互补，引入奇异值分解（SVD）算法使得测距计算更为精确。

对于故障信号的处理，利用故障电压行波信号分量构造Hankel矩阵，对其进行奇异值分解得到SVD第二分量信号，可以准确测量出信号的奇异点，并用SVD脉冲提取出奇异点极值，得到精确的时间信息。根据固有频率法测出的故障点位置的模糊值计算出故障点反射波分别到达两端测量点的时间范围，识别出故障点反射波到达测量点的准确时刻，将时间参数代入测距公式得到测距结果。经仿真验证，该方法有效消除了波速的影响，提高了测距精度。

参考文獻：

[1] 汤广福.基于电压源换流器的高压直流输电技术[M].北京：中国电力出版社，2010.

[2] 葛耀中.新型继电保护和故障测距的原理与技术[M].西安：西安交通大学出版社，2007.

[3] 李泽文，花欢欢，邓丰，等.基于广域行波信息的行波保护[J].中国电机工程学报，2014，34（34）：6238-6245.

[4] 束洪春，邬乾晋，张广斌，等.基于神经网络的单端行波故障测距方法[J].中国电机工程学报，2011，31（4）：85-92.

[5] 蒋洪涛，黄纯，杨帅雄，等.基于小波暂态能量的超高压输电线路暂态保护新方法[J].电网技术，2012，36（8）：248-253.

[6] 韩志锟，饶曙勇，姜玉山，等.基于能量比法的输电线路行波故障测距[J].电网技术，2011，35（3）：216-236.

[7] 宋国兵，蔡新雷，高淑萍，等.高压直流输电线路故障定位研究综述[J].电力系统保护与控制，2012，40（5）：133-137，147.

[8] 徐敏，蔡泽祥，刘永浩，等.基于宽频信息的高压直流输电线路行波故障测距方法[J].电工技术学报，2013，28（1）： 259-265.

[9] 朱永利，范新桥，尹金良.基于三点电流测量的输电线路行波故障定位新方法[J].电工技术学报，2012，27（3）：260-268.

[10] 李博雅，杨耀，杨立红.高压直流输电线路单端故障测距组合算法[J].电力系统保护与控制，2014，42（3）：116-121.

[11] 齐建平.内蒙古500kV输电线路行波故障测距算法研究[D].北京：华北电力大学，2013.

[12] 武晓，何正友，彭少博，等.基于行波固有频率的特高压直流输电线路纵联保护方法[J].电力系统保护与控制，2013，41（11）： 67-73.

[13] 向强铭，王茜，陈靖秋，等.基于奇异值分解理论的双端行波故障测距的研究[J].电力系统保护与控制，2014，42（12）：14-18.

[14] NANAYAKKARA O. Line Fault Location in Emerging HVDC Transmission Systems [D]. Manitoba： University of Manitoba ， 2014.

[15] 赵学智，叶邦彦.基于二分递推SVD的信号奇异性位置精确检测[J].电子学报，2012，40（1）：53-59.

[16] 徐岩，张锐，霍福广，等.基于MAS信息融合的电网故障诊断[J].电力科学与工程，2012，28（9）：24-28.

（责任编辑：杜能钢）