基于量子遗传算法的无人机生命迹象探测研究

朱海斌 许峰

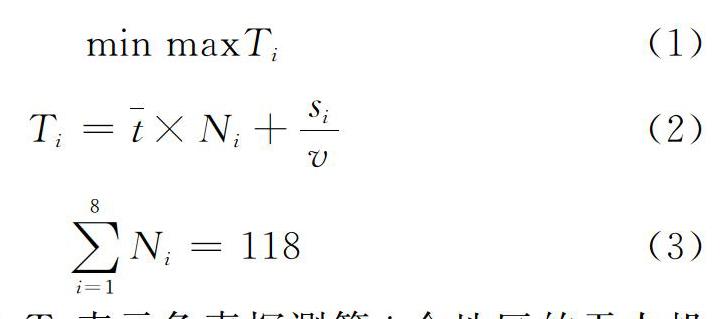
摘 要：针对基本遗传算法易早熟与局部搜索能力欠佳的缺陷，将一种改进的量子遗传算法应用于无人机生命迹象探测路径优化。在基本量子遗传算法的基础上，根据目标函数梯度自适应地确定量子旋转门转角。数值实验表明，该改进算法比基本量子遗传算法有更好的局部收敛性与更快的收敛速度，可获得比基本量子遗传算法更优的生命迹象探测路径。

关键词：无人机；路径规划；量子遗传算法；收敛性

DOI：10.11907/rjdk.173052

中图分类号：TP319

文献标识码：A 文章编号：1672-7800（2018）006-0160-03

Abstract：An improved quantum genetic algorithm is applied to optimize the life sign detection path of UAV. On the basis of the basic quantum genetic algorithm， the rotation angle of the quantum rotation gate is adaptively determined according to the gradient of the objective function. Numerical experiments show that the improved algorithm has better local convergence and faster convergence speed than the basic quantum genetic algorithm， and obtains better life sign detection path than the basic quantum genetic algorithm.

Key Words：UAV； path planning； quantum genetic algorithm； convergence

0 引言

目前，无人机已广泛应用于军事侦察、军事打击、城市规划、资源调查、灾情巡查、生命救援等领域。无人机任务规划中最重要的部分是航迹规划，即在一定的约束条件下，寻找从起始点到目标点的最优路径。合理的航迹规划不仅可以节省资源，提高飞行效率，还可以有效地规避灾害，提高生存概率。

无人机航迹规划常用方法有随机搜索法、Voronoi图法与优化方法[1]。无人机航迹规划是包含复杂约束的大规模优化问题，启发式智能优化算法目前已成为求解航迹规划问题的主要方法，如蚁群算法、粒子群算法、模拟退火算法、遗传算法等。早在1998年，Patcher[2]就讨论了路径规划问题中的关键优化技术及其复杂性；Dong， Zheng和Nikolos等[3-5]研究了路徑规划中进化算法的优化原理；Wu[6]最早将遗传算法应用于航行器路径规划问题；孙阳光等[7]最早将量子遗传算法应用于无人飞行器航迹规划；鱼佳欣等[8]将改进的量子遗传算法应用于无人机航迹规划，获得了较光滑的低代价航迹。

基本遗传算法（SGA）对搜索空间与目标函数要求不高，适用面广，鲁棒性强，具有隐并行性，且全局搜索能力较强。但在求解复杂优化问题时，基本遗传算法经常表现出易陷于局部最优解与局部寻优精度不高的缺陷。因此，本文将一种改进的量子算法（QGA）应用于无人机生命迹象探测规划问题，并根据数值实验对该算法进行性能测试。

1 无人机航迹规划

无人机航迹规划是指在综合考虑无人机的机动性能、碰地概率、突防概率、油耗、威胁与飞行时间约束等各种因素下，找到一条从起始点到目标点的最优可行飞行轨迹。

1.1 无人机航迹规划基本要求

无人机航迹规划核心是从众多飞行航迹中选择满足一系列约束条件的最优航迹，既要减少被敌方摧毁的概率，又要降低自身可能撞地的概率，同时还要满足无人机各种性能的约束条件。一般来说，无人机航迹规划需要考虑下列因素：

（1）突防要求。无人机航迹规划的首要因素是规划航迹的隐蔽性，要使敌方雷达捕获不到无人机，或者虽捕获却不能有效拦截，达到了突防目的。达到突防要求通常采用2种方式：一是使航迹远离威胁源；二是利用地形遮挡降低被敌方探测到的概率。

（2）性能要求。航迹规划必须考虑无人机的性能约束。无人机的性能限制对航迹的约束主要有：①最大转弯角。此参数限制航迹只能在小于或等于该角度范围内转弯；②最大爬升/俯冲角。此参数限制了航迹在垂直平面内上升和下滑的最大角度；③最小航迹段长度。此参数限制了无人机在开始改变飞行姿态之前必须直飞的最短距离；④最低飞行高度。虽然低空飞行可以减少被敌方探测到的概率，但会增加与地面相撞的概率，所以航迹应满足最小飞行高度限制。此外，无人机航迹规划还需考虑燃油限制与通信限制等。

（3）实时性要求。如果预先已掌握了规划区域的完整信息，就可规划出一条从起点到终点的最优航迹。但现代战场环境瞬息万变，不能保证事先所获信息不再发生变化。由于任务的不确定性，无人机有时临时改变飞行任务，而预先规划的航迹则不能满足要求，这将要求无人机航迹规划必须具有实时在线规划功能。

1.2 无人机生命迹象探测问题

本文研究无人机生命迹象探测问题是根据2017年全国研究生数学建模竞赛A题中问题二[9]改编。具体如下：

地震发生后，需使用无人机携带视频采集装置搜索生命迹象，给灾后救援提供准确的目标定位。拟从基地H（110，0），J（110，55）（单位：km）处总共派出8架无人机（各4架），任务完成后回到各自出发地。探测仪有效探测距离不超过1 000m，且最大侧视角（探测仪到可探测处的连线与铅垂线之间的夹角）为60°。规划它们的飞行路线，使附件1所给出的全区域内海拔3 000m以下部分能被探测到的面积尽可能大，从第一架无人机飞出到最后一架完成任务的无人机回到基地的时间间隔尽量缩短。

2 无人机生命迹象探测路径优化问题的改进量子遗传算法

2.1 生命迹象探测路径优化数学模型

由于生命探测仪最大探测距离为1 000m，最大侧视角为60°，根据简单的三角函数关系可得探测带宽为1 732m。

将区域内的结点划分为低于3 000m与高于3 000m两部分。区域最高高度为4 867m，无人机限高5 000m，不存在需要绕飞的区域。对整个区域根据探测带宽提取结点，连同基地H和J共有118个节点。

首先，需要将全部结点分成2部分，使这2部分最优探测路径长度之差尽量缩小，其次将这2部分路径分配给8架无人机进行探测。分配方案满足下列目标与约束条件：

式（1）～（3）中，T-i表示负责探测第i个地区的无人机飞行的总时间，表示无人机探测一个点消耗的平均时间，N-i表示第i个地区内待探测的结点数，s-i表示区域i距离基地的距离，v是无人机的飞行速度。

2.2 基于梯度的自适应量子遗传算法

量子遗传算法是将量子算法引入遗传算法而得到的一种新型智能优化算法，具有高并行性和指数级存储的优点，在计算复杂度与收敛速度方面明显超过其它智能优化算法，用对经典启发式算法进行加速[10]。

在常规量子遗传算法中，编码方式为量子位概率副编码，个体交叉通过量子门的量子比特相位旋转实现，而个体变异则用量子非门代替，所以量子遗传算法的一个主要研究方面是进化策略的构造与编码方式[11]。目前，对基本量子遗传算法的各种改进策略不断涌现，并在许多领域得到了较好的应用[12-14]。

权芳芳等[15]提出了一种基于梯度的自适应量子遗传算法，改进了确定量子旋转门转角大小的方法，其基本思想是：根据目标函数梯度的大小自适应地确定转角步长。当目标函数的梯度较小时，适当增加转角步长，否则适当减小转角步长。这样既可以确保收敛速度，又兼顾了全局收敛性。

基于梯度的自适应量子遗传算法步骤如下[15]：

步骤1：生成初始种群，设定初始转角步长与变异概率。

步骤2：对解空间进行变换，计算出每个染色体的适应度。

步骤3：根据基于梯度的计算方法计算转角大小及方向，从而确定新的量子位。

步骤4：对每个个体，根據变异概率用量子非门进行变异。

步骤5：若达到最大进化代数或满足收敛条件，则停机，否则转步骤2。

3 数值实验结果

根据问题数据，利用基于梯度的自适应量子遗传算法，得出2个区域内1～8号无人机的生命探测最优路径（见图1-图8）。

为评测基于梯度的量子遗传算法在避免过早收敛方面的效果，图9与图10分别给出了基本遗传算法（SGA）与基于梯度的量子遗传算法（GQGA）的进化曲线。图9与图10表明：①GQGA无论在全局收敛性与局部收敛性均全面优于SGA；②SGA至少在2个阶段出现了过早收敛于局部最优解的现象，而GQGA则完全避免了早熟现象。

综上所述，在无人机航迹规划中若采用基于梯度的量子遗传算法，将获得比基本遗传算法更优的航迹规划。

4 结语

本文针对基本遗传算法易过早局部收敛与局部搜索能力较弱的缺陷，在无人机航迹规划问题中引入基于梯度的量子遗传算法。数值实验表明，这种算法在很大程度上克服了基本遗传算法的早熟现象，较好地解决了无人机航迹优化问题。

必须指出的是，基于梯度的量子遗传算法的突出优点是较基本遗传算法有较高的收敛速度。但由于本文所讨论的问题较为简单，这一优点并未充分体现出来。另外，由于遗传算法的理论远未成熟，除了基本遗传算法外，其收敛性无法得以证明，对算法的改进还只能依赖对比实验，这无疑限制和阻碍了遗传算法的进一步研究。

参考文献：

[1] DOBROKHODOV V. Cooperative path planning of unmanned aerial vehicles[J]. Journal of Guidance Control & Dynamics，2014，34（5）：1601-1602.

[2] PATCHER M， CHANDLER P R. Challenges of autonomous control[J]. Control Systems IEEE，1998，18（4）：92-97.

[3] JIA D， VAGNERS J. Parallel evolutionary algorithms for uav path planning[C].Aiaa Intelligent Systems Technical Conference.2013.

[4] ZHENG C， LI L， XU F， et al. Evolutionary route planner for unmanned air vehicles[J]. IEEE Transactions on Robotics，2005，21（4）：609-620.

[5] NIKOLOS I K， VALAVANIS K P， TSOURVELOUDIS N C， et al. Evolutionary algorithm based offline/online path planner for UAV navigation[J]. IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society，2003，33（6）：898-912.

[6] WU X， FENG Z， ZHU J， et al. Ga-based path planning for multiple UAVs[J]. International Journal of Control，2007，80（7）：1180-1185.

[7] 孙阳光，丁明跃，周成平.基于量子遗传算法的无人飞行器航迹规划[J].宇航学报，2010，31（3）：648-654.

[8] 鱼佳欣，李刚，李东涛.改进量子遗传算法在无人机航路规划中的应用[J].计算机仿真，2015，32（5）：106-110.

[9] 2017全国研究生数学建模竞赛试题http：//gmcm.seu.edu.cn/01/49/c12a329/page.htm.

[10] 李士勇，李昐池.量子计算与量子优化算法[M].哈尔滨：哈尔滨工业大学出版社，2009.

[11] 梁昌勇，柏桦，蔡美菊.量子遗传算法研究进展[J].计算机研究进展，2012，29（7）：2401-2405.

[12] 孙海超.改进的量子遗传算法及其在图像匹配中的应用[D].哈尔滨：哈尔滨工业大学，2012.

[13] 符丽锦.量子遗传算法的改进及在货物装配问题中的应用[D].南宁：广西大学，2015.

[14] 赵海洋.基于改进量子遗传算法的认知无线电频谱分配研究[D].秦皇岛：燕山大学，2015.

[15] 权芳芳，许峰.基于梯度的改进量子遗传算法[J].软件导刊，2012，11（8）：31-33.

（责任编辑：刘亭亭）