基于PCA的近邻均值填补优化算法

谢霖铨 毕永朋 廖龙龙

摘 要：均值填补是常用的数据填补方式，但往往忽略了相邻变量之间的相互关系，又对噪声数据极为敏感。将主成份分析算法应用到均值填补算法中，提取相邻各属性的特征重要度，并采用属性重要度作为权重，以均值填补的计算方式算出缺失数据相邻矩阵的加权平均值，将其作为相邻属性对于均值填补的影响偏移值，加入到均值填补的均值计算中。通过对UCI数据集的仿真实验可知，基于PCA改进的算法填补的准确性明显优于均值填补算法。

关键词：近邻均值填补；主成分分析；特征重要度；偏移值

DOI：10.11907/rjdk.172938

中图分类号： TP312

文献标识码：A 文章编号：1672-7800（2018）006-0067-03

Abstract：Mean filling algorithm is a commonly-adopted way to fill missing data. However the correlation between these variables is ignored and also extremely sensitive to noise data. In this paper， the principal component analysis（PCA） algorithm is applied to mean filling algorithm， and the characteristics of adjacent properties are proposed. The weighted mean value of the adjoining matrix of the missing data is calculated by using the attribute importance as the weight. As an adjacent property， the offset value of the mean value is added to the mean calculation of the mean filling. According to results of the UCI dataset simulation experiment， the accuracyof the improved complement algorithm based on PCA is clearly higher than that of the mean filling algorithm.

Key Words：nearest neighbor imputation； PCA； attribute significance； deviant

0 引言

缺失数据指在数据采集时由于某种原因，应该得到而实际没有得到的数据，导致现有数据集中某个或某些数据不完全。

數据处理需要建立在完备数据上，但在现实数据整理收集过程中，收集的数据很难避免缺失问题。这些缺失的数据给后续数据分析带来巨大影响，特别是分析过程和所得结果的准确性。所以，在数据处理分析之前，对缺失数据的预处理成为一项很重要的准备工作[1]。常用的缺失数据处理方法有删除缺失数据或对缺失数据进行填补。为不影响其它有效数据，一般会采用数据填补。数据填补方法是利用其它辅助信息，经过计算，得到一个新的数值，插入缺失位置来代替缺失值。根据所构造数值的个数，可分为单一填补和多重填补[2]。

近年来，数据填补不再简单地以数据的数值大小作为计算准则，基于粗糙集合理论[3]、相似关系、关联规则[4]等理论，更多的改进算法相继被提出来[5]。

最近邻均值填补是一种单一填补的方法，操作简单，深受广大研究者青睐[6]，但受噪声影响比较大。文献[7]介绍了一种基于噪声处理的近邻填补算法。

主成份分析（principal component analysis，PCA）是Karl Parson[8]于1901年提出的一种经典特征降维算法和多元统计分析方法。根据原始数据集的协方差矩阵和特征值特征向量，计算新的向量基，最终将原始数据投影到新的向量基中，并使这些新变量尽可能多地反映原变量的信息量。文献[9]采用PCA的思想对水质数据之间蕴含相似性进行剖析，并找出其影响水质状况的各个指标的相似程度大小。文献[10]则使用PCA算法处理属性相关的问题，借鉴PCA算法的压缩原理，通过算出协方差矩阵的特征值特征向量，找到主要元素，并计算各属性权重，加入到其它算法中，以此排除无关属性的干扰。

由于均值填补算法也常受无关属性干扰和噪声数据的影响，使找到的替代值偏大或偏小。基于以上研究，将PCA算法融入到最近邻均值填补算法中，以新的向量基下的数据集属性方差贡献率为权值，计算邻近数据整体的影响值，提高填补效果，可有效克服噪声和无关属性对填补结果的影响。

1 最近邻填补

最近邻填补是在图像处理中常用的数据填补算法。原理是选择未知像素一定范围内的K个近邻像素数据作为目标数据的最近邻，把K个最近邻像素数据的平均值作为目标数据缺失像素的替代值。

最近邻填补算法流程：

（1）整理数据集（包含有缺失项的数据记录）。

（2）查找数据集中有缺失的数据项，找到缺失数据的近邻数据x-1，x-2，…，x-k。

（3）计算K个最近邻数据的和。

（4）将均值M=S/k作为缺失值的替代值，填补到缺失位置。

（5）重复（2）～（4），直到数据集中不再含有缺失数据为止。

2 PCA算法

PCA算法是一种无监督降维学习方法，通过抽取样本的主要影响因素，简化复杂的问题。

PCA的基本原理是：

（1）将原始数据集按列组成m行n列矩阵X。

（2）将X的每一行进行零均值化，即减去这一行的均值：

（3）求出协方差矩阵C：

m代表样本个数

（5）计算特征贡献率：

（6）将特征向量按对应特征值大小从上到下按行排列成矩阵，组成矩阵P。

（7）Y=PX即为降维到k维后的数据。

3 PCA改进的均值填补算法

基于PCA的最近邻填补算法，是依靠原始样本数据，得到缺失值的替代值，在填补效果上有良好的表现。它的主要思想是根据缺失值的近邻值，通过PCA算法计算出一个基于属性特征值的影响值，作为一个额外的特征偏移值加在均值算法最后的计算中。该算法主要分为3个阶段。

3.1 第一阶段算法

（1）首先数据初始化，构建完整的数据矩阵X，并将所有缺失数据标记为-1以待下一步处理。

3.2 第二阶段算法

PCA算法会把贡献率特别低的无关属性以及噪声剔除，而且不会影响数据的整体特性，减少噪音和冗余，降低过度拟合的可能性。通过PCA算法对近邻矩阵L分析，将数据映射到新的维度下，生成新的5*5数据集N。

（1）进行标准化矩阵L主成份分析，得到各特征值λ-1和主特征贡献率e-i，及由特征向量d-i构成的转换矩阵P。

（2）映射到新数据集：

（3）求出其它属性值对缺失值属性的影响偏移值，既每个属性特征重要度和属性值乘积的加权和的均值。

n-ij是矩阵N中的元素，k是特征值个数，25是所选取的缺失值近邻数据个数24加上缺失值本身，即矩阵N的数据个数。

3.3 第三阶段算法

利用均值填补算法计算最近邻数据的数值和，在计算替代值M算法的基础上加上特征影响偏移量m，得到新的填补值M′。

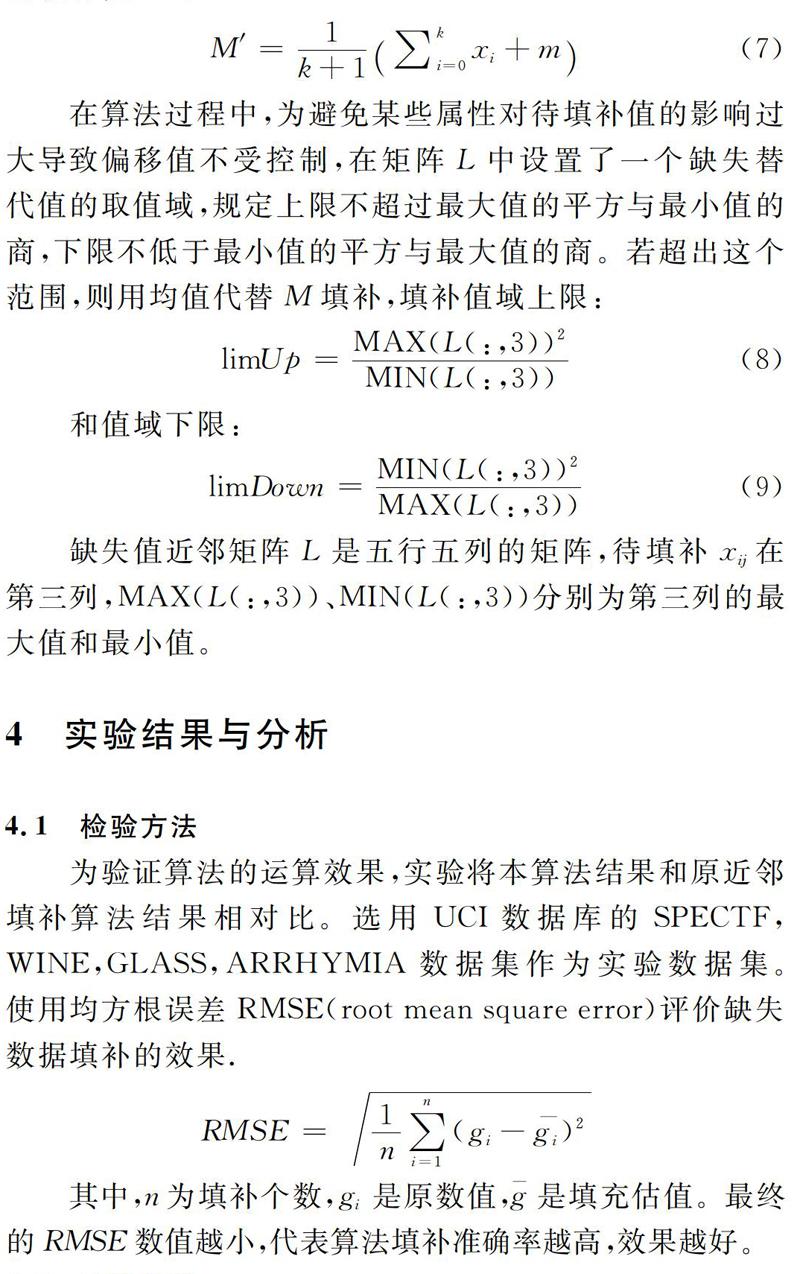
在算法过程中，为避免某些属性对待填补值的影响过大导致偏移值不受控制，在矩阵L中设置了一个缺失替代值的取值域，规定上限不超过最大值的平方与最小值的商，下限不低于最小值的平方與最大值的商。若超出这个范围，则用均值代替M填补，填补值域上限：

4 实验结果与分析

4.1 检验方法

为验证算法的运算效果，实验将本算法结果和原近邻填补算法结果相对比。选用UCI数据库的SPECTF，WINE，GLASS，ARRHYMIA数据集作为实验数据集。使用均方根误差RMSE（root mean square error）评价缺失数据填补的效果.

其中，n为填补个数，g-i是原数值，是填充估值。最终的RMSE数值越小，代表算法填补准确率越高，效果越好。

4.2 实验结果

为了测试实验结果的准确性，本实验设置不同的缺失比例，缺失率分别为5%、10%、15%、20%、25%、30%、35%、40%、45%、50%、55%。为使结果准确，取多次实验的均值。通过Matlab仿真实验得到对比结果。

三角形折线表示原始均值算法填补实验效果，正方形折线代表改进算法实验效果，图1、图2、图3分别是3种不同类型数据集下的实验结果。

由实验结果可知，基于PCA改进后的填补算法在准确度上有明显提升，总体上优于之前算法。在WINE和GLASS数据集仿真中，优化后的算法结果明显更平稳，缺失比例从5%上升到55%的过程中，衡量填补效果的均方根更趋于平缓。

5 结语

基于PCA算法的最邻近算法与原始均值算法相比，通过对均值计算的加权，并设置上限值和下限值，更好地解决了噪声或冗余数据数据对结果造成影响的问题。

不过，该算法也有不足之处，在对类似于数据集SPECTF这种噪声数据较少、数据集数值比较平均的缺失数据填补时，增大了工作量和时间复杂度，填补效果也并没有有效提高，在以后的工作中将会继续对算法研究改进以达到更好的效果。

参考文献：

[1] ALLISON P D.缺失数据[M].林毓玲，译.上海：格致出版社，2012.

[2] 庞新生.缺失数据插补处理方法的比较研究[J].统计与决策，2012（24）：18-22.

[3] 武森，冯小东，单志广.基于不完备数据聚类的缺失数据填补方法[J].计算机学报，2012，35（8）：1726-1738.

[4] 于力超，金勇进，王俊.缺失数据插补方法探讨——基于最近邻插补法和关联规则法[J].统计与信息论坛，2015，172（1）：35-40.

[5] 毛玫静，鄂旭，谭艳，等.基于属性相关度的缺失数据填补算法研究[J].计算机工程与应用，2016，52（6）：74-79.

[6] PAN R， YANG T， CAO J， et al. Missing data imputation by K nearest neighbours based on grey relational structure and mutual information[J]. Applied Intelligence，2015，43（3）：614-632.

[7] 郝胜轩，宋宏，周晓锋.基于近邻噪声处理的K-NN缺失数据填补算法[J].计算机仿真，2014，31（7）：264-268.

[8] BERNSTEIN H J， ANDREWS L C. Accelerating k-nearest-neighbor searches[J]. Journal of Applied Crystallography，2016，49（5）：1471-1477.

[9] 董建华，王国胤，姚文.基于PCA的水质数据相似度分析模型[J].环境工程，2016（s1）：841-844.

[10] 黄秀霞，孙力.基于属性依赖度计算和PCA的C4.5算法[J].传感器与微系统，2017，36（1）：131-134.

（责任编辑：江 艳）