基于多元回归模型的不同浓度物质颜色分量分析
2018-09-04郭正尧李示威程东海刘桂国杨洪壮
刘 令 郭正尧 李示威 程东海 李 昊 刘桂国 杨洪壮 黄 元
(吉林建筑大学,长春 130118)
生活中,我们经常需要测量某一物质的浓度,比色法是目前检测物质浓度较为常用的一种方法,即把待测物质制成溶液滴在特定的白色试纸表面,再把该试纸与一个标准比色卡进行比对,就可以确定待测物质的浓度,但此法需要用肉眼观测,致使精确度太低,伴随着颜色分辨率和照相技术的逐步提高,我们可以相对准确地得到待测物质的颜色分量(红、绿、蓝、色调、饱和度),最终确定待测物质的浓度.
1 多元回归模型的建立[1]
在回归分析中,如果有两个或两个以上自变量,就称为多元回归.本文讨论物质浓度与5个颜色分量的关系,我们考虑到由多个自变量的最优组合共同来预测物质浓度,比只用一个自变量进行预测更有效,更符合实际,故本文采用多元回归模型解决问题.
设无量纲物质浓度为y,无量纲颜色分量为xi(i=1,2,3,4,5),颜色分量系数为βi(i=1,2,3,4,5),计算后的无量纲截距为β0,多元回归模型的一般表现形式为:
y=β0+β1x1+β2x2+β3x3+β4x4+β5x5
2 模型的求解[2]
为了得到物质各浓度所对应颜色分量的读数,本文采用绿红蓝(Green red blue,英文缩写为GRB)图像颜色检测技术,即可以得到绿红蓝3种颜色分量的读数,然后通过色空间转换算法[3]可以得到色调和饱和度两种颜色分量的读数,将颜色分量的数据导入MATLAB中,得到无量纲截距和颜色分量系数(见表1).

表1 各物质通过回归模型确定的回归系数Table 1 Regression coefficient determined by linear regression model for eachsubstance
截距为各种物质的最小覆盖浓度,当物质浓度达到此值时,颜色读数等于0(溶液的透光性为0),不会随着浓度的提高发生明显的变化,表1中β1至β5数值为各颜色读数的回归系数,由这些数据可得到相应物质的回归方程,即多元回归模型,现以二氧化硫为例,其形式为:
y=2 150.8-7.2x1-7.4x2+0.2x3+0.5x4+4.0x5
(1)
其他物质也可以用同样的方法得出函数表达式.
3 残差检验[4]
本文利用残差(在数理统计中是指实测值与计算值之间的差)分析法判断数据的优劣,将数据导入MATLAB中,用多元回归分析函数Regress导出浓度和五个颜色分量的关系式,得到残差函数Rcoplot,然后输出函数的数据残差图.

图1 硫酸铝钾残差Fig.1 Residual of potassium aluminum sulfate
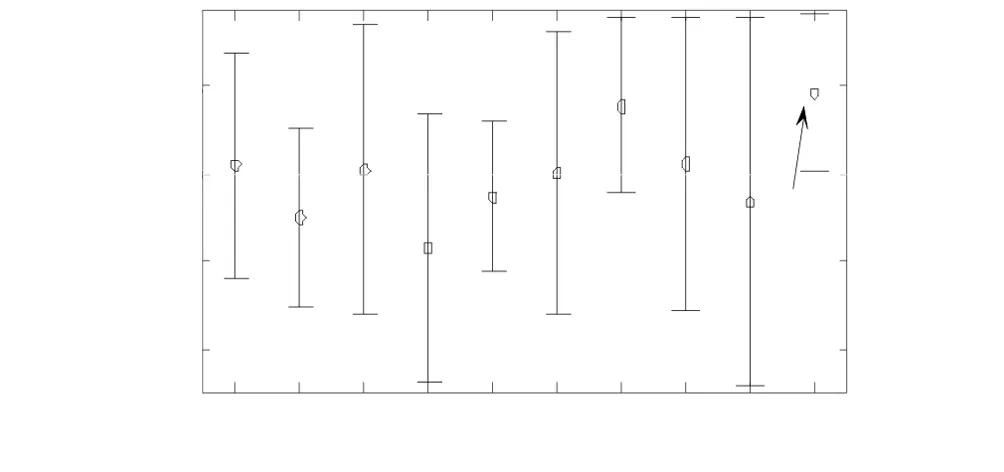
图2 溴酸钾残差Fig.2 Residual of potassium bromat
用箭头指出的是误差较大的点,没有标注的是合理数据的残差图,线长代表了每点的置信区间.置信区间越小,说明有效性越好,若含零点,说明结果无效.
利用残差分析法并结合图1与图2,可以清楚地看出硫酸铝钾与溴酸钾对比,硫酸铝钾的置信区间小,所以硫酸铝钾的数据更好,可靠性更高.
4 模型误差分析[5]
本文进一步对多元回归模型进行误差分析,先将数据[4]导入MATLAB,然后根据(1)式计算出预测浓度值,并导入MATLAB中,得到图3.
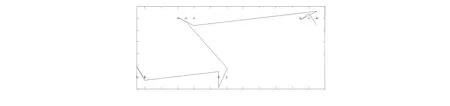
图3 二氧化硫的实测值与计算值Fig.3 Measured yalue and calculated value for sulfur dioxide
图3中加号代表实测点,折线代表(1)式的图像,这幅对比图有助于直观地观测计算值与实测值之间的联系与差异.从图3可以看出,通过该模型求出的计算值与实测值非常接近,但仍然存在误差.为了检验模型与数据[4]的拟合程度,本文采取拟合优度检验法[5]来说明拟合度,构造一个表征拟合程度的指标R2,统计量R2定义为:
式中,S1(总变差平方和)是各个实测值与样本均值之差的平方和,S2(残差平方和)是总变差平方和中不符合(1)式的部分.
根据MATLAB求出R2等于0.975 3,R2越接近于1,表示模型拟合程度越高,由此看出所求的模型合理,可以推广使用.
5 结语
经过全文论述可知,运用多元回归模型可得出二氧化硫的浓度与颜色分量的关系式,可以较为准确地得出二氧化硫的浓度,由最小覆盖浓度的大小可知物质透光性的强弱,诸如硫酸铝钾,溴酸钾等其他物质也可通过这种方法得到相应的结果,体现了多元回归模型广阔的应用前景.
