基于ABAQUS的抗滑桩加固边坡的数值模拟分析
2018-09-03曾晋
曾 晋
(成都理工大学 工程技术学院,四川 乐山 614000)
滑坡不仅会对农业生产、建筑物造成经济损失,同时也会造成人员伤亡,因此对边坡稳定性的研究一直受到工程和学术界的广泛关注。目前,主要通过排水措施、削坡减载,填土、锚杆支护、支挡结构、抗滑桩等方式对边坡进行加固分析。经过长时间的研究和论证,发现抗滑桩对边坡进行加固具有较大的优势,但是目前对于抗滑桩加固边坡的研究刚刚起步,并且各个学者研究的结果也不尽相同。因此,本文基于ABAQUS软件采用强度折减法对抗滑桩加固边坡进行模拟分析,研究桩位、桩间距与桩径比、桩长等因素对边坡安全系数以及边坡失稳时滑裂面出现位置的影响。
1 边坡土体的数值模型理论分析
本文基于强度折减法和极限平衡方法分析土质边坡,通过有限元软件ABAQUS进行边坡的稳定性分析,利用ABAQUS提供的弹塑性理论模型和屈服准则判断不同屈服准则下的安全系数。数值计算方法可以分析不同影响因素对边坡稳定性的影响,不仅可以定性研究边坡稳定性问题,也能够进行一定的定量分析。随着计算机技术的快速发展,采用数值分析方法对边坡稳定问题进行研究也有了长足的进步。见图1。

图1 有效莫尔应力圆
ABAQUS提供了多种土体本构模型,其中摩尔-库伦本构模型主要考虑不光滑小表面的情况,较为真实反映了土体的应力-应变的特点。通过大量的试验研究表明,图1为可以用有效应力表示土体破坏的莫尔应力圆,莫尔圆公切线为一条直线,这条直线的公切线被称为莫尔-库伦破坏准则,其表达式如下:

根据图1中几何关系,得到如下式:
上式中的莫尔-库伦破坏准则在M-C模型中用作屈服函数,该函数为一个不规则的六凌锥,见图2。

图2 M-C屈服面
有效主应力通过不变量表示如下:
2 数值模型
根据工程实例,对均质黏性土边坡进行几何模型建立,根据试验和规范得到土体的计算参数见表1。

表1 土体参数表
数值计算模型见图3。模型尺寸为:边坡的前缘长和高度分别为L1=30 m,H1=42 m;边坡的坡体在水平投影长度L2=24 m,坡体后缘长度为L3=45 m,边坡前后、左右4个面进行法向位移约束,底面进行3个方向的全约束,土体选用理想弹塑性本构模型进行分析。

图3 边坡土体的计算模型
3 抗滑桩数值模拟结果分析
3.1 最优桩位和合理桩间距的确定
由于边坡加固的复杂性,运用抗滑桩对边坡进行加固,加固的最优位置以及合理间距具有较大的差异。不同学者的研究具有不同的结果,还未达到统一的判断标准,因此对抗滑桩的加固位置以及合理间距进行研究具有重要的意义。通过控制桩间距S与桩阻滑边B的比值分别为1、2、3、4、5和6来改变抗滑桩在坡体中的位置,采用ABAQUS软件的强度折减方法,自动搜索边坡的安全系数,得到边坡的整体安全系数,见图4。

图4不同影响因素与安全系数的关系
由图4可知,当桩位位于边坡中部往下位置时,安全系数迅速增加,这主要是抗滑桩的加固起到了一定的作用。通过对图4曲线进行拟合,得到二次曲线方程,进一步探究最大安全系数的具体位置。见表2。
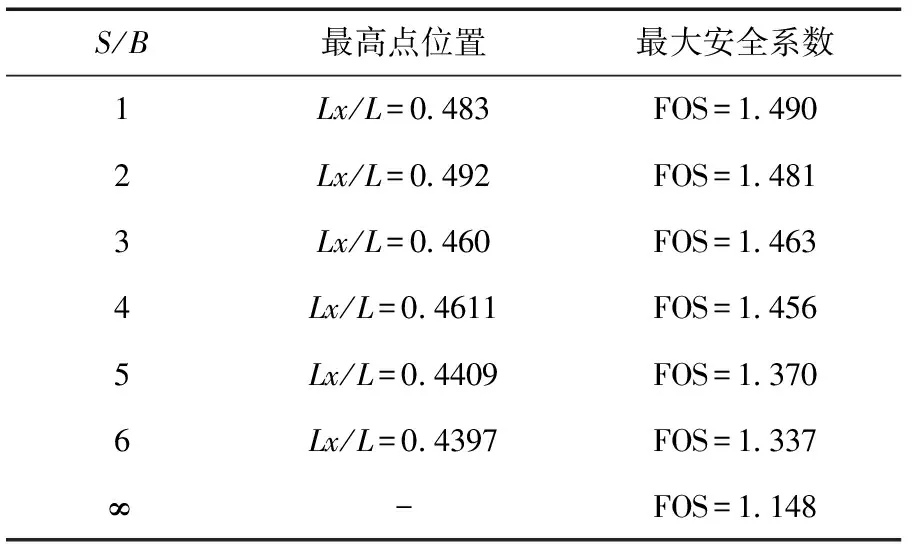
表2 不同S/B下最大安全系数表
根据以上拟合分析可知,当S/B=1~4时,边坡的最大安全系数接近坡中;随着S/B的减小,这个现象越明显。随着S/B的增大,边坡的安全系数逐渐降低,边坡桩的最大安全系数位置向下移动;当S/B增大到一定程度时,近似认为边坡处于无桩加固状态,此时边坡及其不稳定,极易出现失稳等情况。不论加固桩处于什么位置时,安全系数随桩间距和S/B的增大而减小,现取S/B=2不同桩位出现塑性变形图进行分析。见图5~图6。
图5为抗滑桩位于斜坡下半部分时的塑性变形图,图6为抗滑桩位于斜坡上半部分时的塑性变形图。由图5~图6可知,当抗滑桩位于Lx/L=0~1时,坡体出现临界的滑裂面,以抗滑桩为界将坡体分为两个部分,当抗滑桩与处于中间位置时,边坡产生的塑性变形最小,此时抗滑桩的阻滑效果更为有效。当抗滑桩位于坡脚或者坡顶附近时,边坡的塑性区滑裂面基本上呈一条圆弧形曲面分布,此时抗滑桩的阻滑效果与无抗滑桩的边坡非常接近。因此,在仅仅考虑边坡的安全性,抗滑桩的最优加固位置Lx/L=0.4左右,此时的边坡的加固效果最佳。但在工程中不仅要考虑到安全性,同时也要考虑到经济、资源配置等因素,通过结合以上分析,最优加固位置Lx/L=0.2~0.4处,综合边坡加固效果最佳。
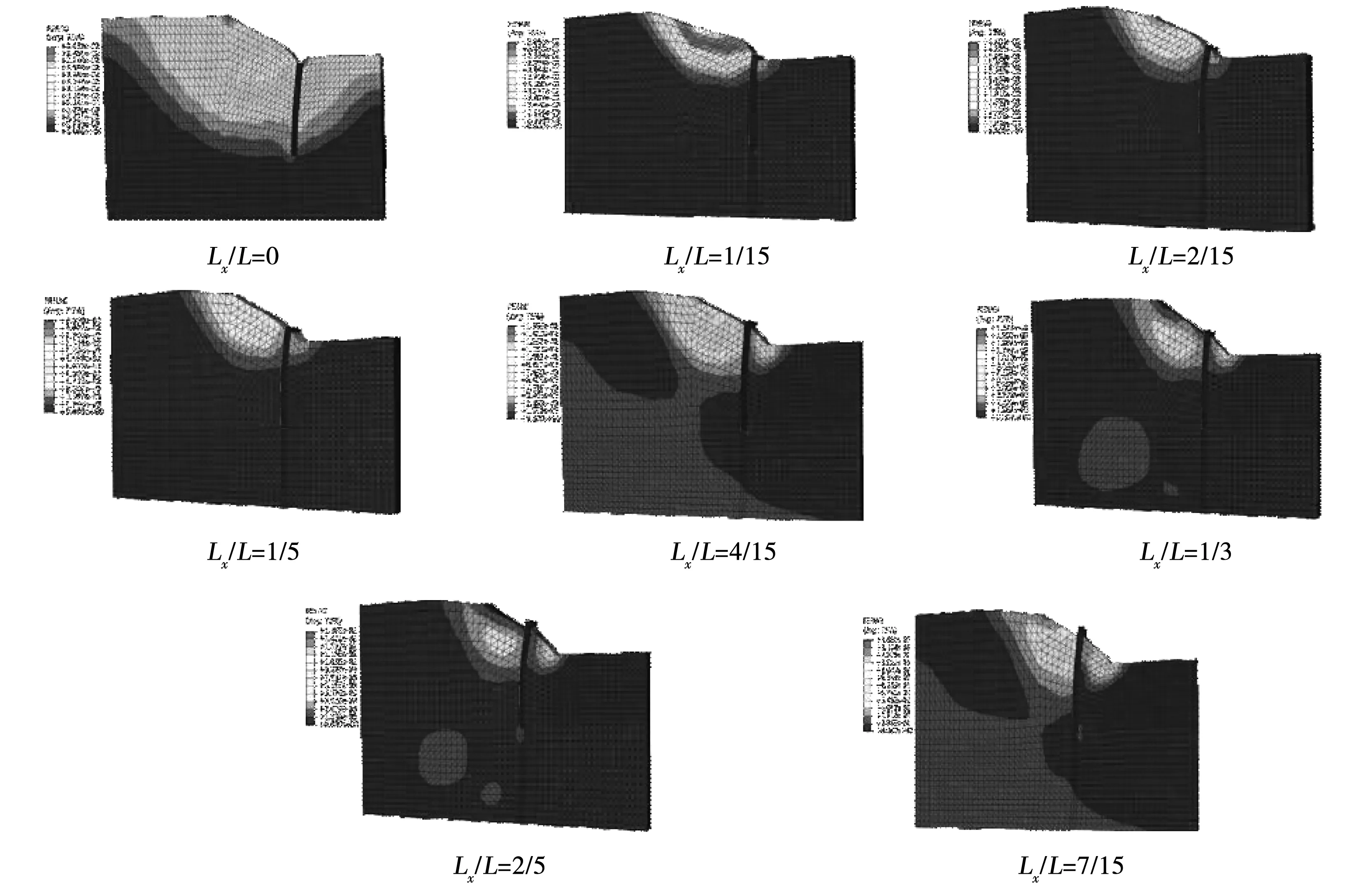
图5 抗滑桩位于斜坡下半部分的塑性变形图

图6 抗滑桩位于斜坡上半部分的塑性变形图
3.2 不同桩长结果
根据3.1节的分析可知,抗滑桩位于边坡的最优位置Lx/L=0.4处,保证桩的横截面积和桩间距相同的情况下,改变抗滑桩的长度分别为6、10、14、16、18、22和26 m共6组进行对比分析,桩长对边坡安全系数及塑性变形滑裂面的影响见图7。

图7 加固桩长与边坡安全系数的变化关系
由图8可知,抗滑桩长度Lp<16 m时,边坡塑性滑裂面均完全包裹住抗滑桩,此时抗滑桩对边坡的抗滑效果非常差,边坡的抗滑性能相当于无抗滑桩加固状态下的边坡的抗滑性能,这一点从边坡的安全系数就可以看出,抗滑桩长度小于16 m时的安全系数跟无抗滑桩加固的边坡的安全系数较为接近。当抗滑桩长度在16~18 m时,边坡的塑性滑裂面恰好没有通过抗滑桩底,并且滑移线没有向下移动,其安全系数速速上升,此时抗滑桩的抵抗滑移效果非常明显,抗滑桩桩底位于滑移线以下,因此此时抗滑桩具有一定的锚固作用。
由图7可知抗滑桩的长度与边坡安全系数呈现分段线性关系,当抗滑桩长度在0~16 m时,线性增长速度极小;当抗滑桩长度在16~18 m时,安全系数发生突变;抗滑桩长度在18~30 m时,安全系数进一步增大。但是相对16~18 m时较缓一些。

图8 不同抗滑桩长度下斜坡上半部分的塑性变形图
由图7和图8可知,抗滑桩长度在16~26 m时,边坡的安全系数增长明显,随着长度的继续增加,边坡的安全系数增加非常缓慢。这主要是抗滑桩的长度达到一定程度之后它的抗滑能力达到最大,随着抗滑桩长度的继续增大,土体的抗剪强度降低,抗滑桩的侧压力会增大,因此桩体可能发生破坏,进而导致边坡的安全系数增加并不明显。通过以上分析可知,抗滑桩长度在22~26 m较为合适,抗滑桩的锚固深度为4/11~5/13桩长较为合理。
4 结 论
本文通过ABAQUS数值计算对抗滑桩加固边坡的最优桩位、桩间距和桩长进行了模拟分析,结论如下:
1) 当桩间距S与桩阻滑边B比值为1~4时,边坡的最大安全系数接近坡中;随着S/B的增大,边坡的安全系数逐渐降低,边坡桩的最大安全系数位置向下移动;当S/B增大到一定程度时,近似认为边坡处于无桩加固状态,此时边坡及其不稳定,极易出现失稳等情况,不论加固桩处于什么位置时,安全系数随桩间距和S/B的增大而减小。
2) 在仅仅考虑边坡的安全性,抗滑桩的最优加固位置Lx/L=0.4左右,此时的边坡的加固效果最佳。但是在工程中不仅要考虑到安全性,同时也要考虑到经济、资源配置等因素,通过结合以上分析,最优加固位置Lx/L=0.2~0.4处,综合边坡加固效果最佳。
3) 当抗滑桩长度在0~16 m时,线性增长速度极小;当抗滑桩长度在16~18 m时,安全系数发生突变;抗滑桩长度在18~30 m时,安全系数进一步增大,但是相对16~18 m时较缓一些。抗滑桩长度在22~26 m较为合适,抗滑桩的锚固深度为4/11~5/13桩长较为合理。
