基于定位标签的时间规整方法*

钱宇红，许士敏，储飞黄

（国防科技大学 电子对抗学院，安徽 合肥 230037）

0 引 言

在话音通信系统中，由于受到系统传输特性和干扰信号的影响，输出信号必然会产生失真。为了评估话音通信系统的性能，通常需要比较输入语音与输出语音的相似度。信号传输和处理需要时间，导致发送与接收之间很难在时间上实现精确同步。所以，输入信号和输出信号之间不可避免地存在延时。如果不能使输入信号与输出信号在时间上精确对齐，即使输出信号没有失真，比较的结果误差也会非常大。使输出语音信号与输入语音信号在时域上精确对齐的过程就是时间规整。时间规整的本质是估计并消除输出语音信号与输入语音信号之间的时间延迟。通常情况下，语音信号处理以帧为基本分析单元，且帧长取值范围为25～64 ms，时间规整的误差应远小于帧长，一般要求小于3 ms[1]。

1 时间规整

时间规整是衡量两个时间序列之间相似度所采取的方法，现在广泛使用动态时间规整算法（Dynamic Time Warping，DTW）。DTW采用动态规划思想，通过把时间序列进行延伸和缩短，使两个时间序列中所有对应点的距离之和最小，以此衡量两个时间序列之间的相似性。DTW在孤立词识别系统中得到了广泛应用[2]，但当环境噪声增大时，识别性能会急剧下降，甚至无法工作。例如，Dautrichr[3]等演示的孤立字词识别系统在安静环境下的识别正确率可达95%，而当信噪比为18 dB时，正确率下降到60%左右。又如，由纯净语音训练得到的一个孤立词语音识别系统，在相对安静环境下识别正确率可达100%，而在以90 km/h速度行驶的汽车内使用时识别率骤降到30%[4]。产生上述现象的一个重要原因，是用DTW算法进行时间规整的适应性差，对环境依赖性强。当环境改变时，系统性能下降；在强噪声环境下，系统几乎不能工作[5]。因此，本文提出了一种基于定位标签的时间规整方法。与传统的时间规整方法相比，提出的方法时间规整精度高，在低信噪比条件下仍能获得较高的时间规整精度。

2 基于定位标签的时间规整原理

构造一种基于正交正弦脉冲序列的定位标签，把标签插入原始语音信号前，与原始语音信号一起组成输入信号，并送入话音通信系统，把得到的输出信号与定位标签进行互相关运算，根据互相关运算的最大值位置估计系统时延，从而实现话音通信系统输入与输出信号的时间规整。

定位标签信号l(t)的构成为：

式中，f0为正交正弦脉冲序列定位标签的基频，T0=1/f0为基频周期，φ0为每个正弦脉冲序列的初始相位，u(t)为阶跃函数。Kf0是脉冲序列中最高的频率分量，K和f0的选取必须保证标签信号能够通过话音通信系统传输。

定位标签l(t)是利用三角函数集{sin(Ωt),sin(2Ωt),…,sin(nΩt),…}中任意两个函数在区间内正交的性质构成的。

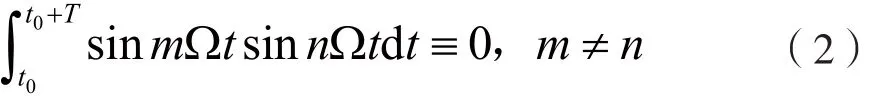
l(t)具有如下特征：

（1）定位标签由一组确定的正弦脉冲序列组成，正弦脉冲序列各分量之间两两正交，每个脉冲序列的时间长度均等于T0；

（2）定位标签的自相关函数具有尖锐的峰值，K值越大，峰值越高；

（3）定位标签与语音、噪声及自身时间延时序列的相关度很低，所以具有很好的标签和抗噪能力。

设原始语音信号为s(t)，在s(t)的起始位置之前插入定位标签信号l(t)，形成了输入信号x(t)：

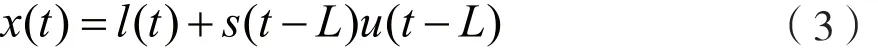
式中，L为定位标签的时长，L=KT0。经过系统传输和解调处理，输出信号中包含了定位标签信号、语音信号和噪声信号。把输出信号与定位标签进行互相关运算，实际上就是定位标签的自相关运算和定位标签与语音、噪声和自身延时的互相关运算。由于定位标签有尖锐的自相关峰，而定位标签与语音信号和噪声信号的互相关度很低，即使在低信噪比环境下也可以准确估计系统时延，从而实现话音通信系统输入与输出信号的时间规整。

3 基于定位标签的时间规整原理框图及过程

3.1 基于定位标签的时间规整原理

以语音测试信号x(t)为话音通信系统的输入信号，将系统的输出语音信号y(t)与定位标签l(t)进行互相关运算，然后将互相关函数取得最大值的位置偏移量作为话音通信系统时延τ0的估计值τ^0，进而以τ^0+L为起点，从话音通信系统的输出语音信号y(t)中截取与原始语音信号s(t)等长度的信号作为测试语音的时间规整后的输出响应，再送入下一步的失真度评估模块，如图1所示。

图1 插入定位标签的时间规整原理

3.2 基于定位标签的时间规整过程

3.2.1 定位标签设计

正交正弦脉冲序列定位标签l(t)的构成如式（1）所示。为了保证定位标签的高性能，必须让定位标签能高保真地通过系统，通常应确保定位标签最高频率分量Kf0的三次谐波3Kf0能通过系统。假设被测系统允许的基带信号最高频率fmax为4.0 kHz，可以合理选取f0=40 Hz，K=30。于是，定位标签由30个正弦脉冲串构成，时间长度L为750 ms，得到波形如图2所示，其自相关特性如图3所示。可以看到，定位标签尖锐的自相关峰值。

图2 定位标签波形

图3 定位标签自相关波形

3.2.2 生成语音测试信号

图4为一段原始语音信号仿真s(t)，插入定位标签后生成语音测试信号x(t)（如式（3）所示），波形如图5所示。

图4 原始语音信号s(t)

图5 插入定位标签的语音测试信号x(t)

3.2.3 将语音测试信号输入话音通信系统并存储系统的输出信号

为了研究本算法的时延估计精度，把输入语音测试信号x(t)时延500 ms，并加入比信号低18 dB的高斯白噪声作为话音通信系统的输出信号y(t)，如图6所示。

图6 输出语音信号y(t)

3.2.4 时延估计

将系统输出信号y(t)与定位标签l(t)进行互相关运算，把互相关函数取得最大值的位置代表的时延作为系统时延估计值τ^0。图7为本例中定位标签与输出信号y(t)的互相关函数波形，可得互相关函数取得最大值的位置为500 ms，即本例中时延估计没有误差。实际应用系统中，接收系统采样会产生一定误差，一般很小。

图7 输出信号与定位标签的互相关波形

3.2.5 平移、截断

根据时延估计值τ^0和输入信号长度从输出信号中截取有用信号。在系统输出语音信号y(t)中，以500 ms再加上定位标签的长度750 ms即1 250 ms为起点，截取与原始语音信号等长的信号，得到了时间规整后的输出语音信号，如图8所示。此时，经过时间规整后的输出语音信号与输入语音信号在时域上精确对齐，可以进入下一步的失真度评估模块，评估输出语音信号的失真度。

图8 时间规整后的语音信号

4 时延估计误差与信噪比

为了研究本算法时延估计误差与信号信噪比的关系，将输出信号加上不同信噪比的白噪声，然后和定位标签分别进行互相关运算，比较在低信噪比下的时间对齐精度，结果如图9、图10所示。

图9 不同信噪比下的互相关函数

图10 时延估计误差与信噪比关系

由仿真结果可得：对信噪比大于-5 dB的信号，时间规整的误差小于0.1 ms；当信噪比大于-20 dB时，时延估计误差小于0.125 ms，满足时间规整的误差要求；当在信噪比小于-23 dB后，时间规整的误差会急剧增大。可见，基于正交正弦脉冲序列定位标签的时间规整方法，能够应用于信噪比最低达-20 dB的低信噪比话音通信环境。

5 结 语

基于定位标签的时间规整方法计算简单，时间规整精度高，尤其是当信噪比为-20 dB时，仍能达到非常高的精度，远远超过传统方法的时延估计精度，具有很强的抗干扰能力。