基于无量纲水流强度指标的坡面流输沙能力计算方法

高晨烨，张宽地,，杨明义



基于无量纲水流强度指标的坡面流输沙能力计算方法

高晨烨1，张宽地1,2※，杨明义2

（1. 西北农林科技大学旱区农业水土工程教育部重点实验室，杨陵 712100；2. 西北农林科技大学黄土高原土壤侵蚀与旱地农业国家重点实验室，杨陵 712100）

坡面水流输沙能力是土壤侵蚀模型的重要参数之一，也是土壤侵蚀精确预报的基础。该文选用多沙粗沙区典型黄土（中值粒径50=0.095 mm，50′=0.04 mm）进行了坡度范围为7%～38.4%，单宽流量范围为0.000 14～0.005 26 m2/s的水槽模拟输沙试验，经无量纲化处理后分析了坡面水流输沙能力与坡度和单宽流量以及输沙能力与各水流强度指标间的耦合关系。结果表明：坡面水流输沙能力与坡度、单宽流量呈幂函数关系（2=0.955），且单宽流量较坡度而言对输沙能力的影响更为显著；含沙水流平均流速与坡度、流量呈幂函数关系；剪切力可以通过幂函数关系式预测坡面水流输沙能力（2=0.900，N=0.756 1）；水流功率、有效水流功率是比剪切力更好的预测因子，其中考虑临界水流功率0=36.5，水流功率与输沙能力幂函数关系（2=0.950，N=0.978）最佳；单位水流功率并不能作为预测输沙能力的水流强度指标。该文关于黄土丘陵沟壑区坡面水流输沙能力的研究为土壤侵蚀预测模型提供了新的方法。

土壤；侵蚀；径流；坡面流；输沙能力；水流强度指标；水流功率

0 引 言

目前，土壤侵蚀已经发展为全球性的环境问题，据不完全统计，全世界范围内每年因土壤侵蚀损失的耕地高达5 000～7 000 km2[1-2]，而中国是世界上土壤侵蚀最严重的国家之一，且在黄土高原地区表现尤为突出[3-5]，该问题已经严重制约了当地社会经济的可持续发展。土壤水蚀作为土壤侵蚀最主要的方式，是指土壤在水流作用下，土体结构剪切破坏、颗粒被水流携带的过程，其过程主要包括土壤颗粒分离，泥沙输移和沉积3个动力过程。而水流含沙量与输沙能力两者的协调作用直接制约着这3个动力过程。所谓的坡面水流输沙能力主要是指在特定坡度特定流量下运输泥沙的最大通量[6-7]，它是判别泥沙颗粒是否发生剥离、搬运或沉积的临界量，也是土壤侵蚀过程模型的重要控制参数之一[8]。因此，准确预测评估坡面水流输沙能力是阐明土壤侵蚀的关键科学问题之一。

综合相关学者研究发现，影响坡面水输沙能力的主要因子包括坡度、流量以及泥沙颗粒中值粒径[9-10]。Meyer等[11]通过4组不同中值粒径的犁沟梯度试验发现梯度较流量而言对输沙能力的影响更大，且泥沙输移量随中值粒径的减小而增加；雷廷武等[12]也得出坡度为主要影响因子；但Zhang等[13]和Aziz等[14]等却得出流量对输沙能力影响更大。为了规避水面波动等非恒定强度对输沙能力的影响，研究学者多采用平均水流强度指标来建立坡面水流输沙能力。泥沙运动学中，水流强度指标可归纳为3类：流速类指标（平均流速、近底流速及表流速）、动力学类指标（剪切力）和功率类指标（单位水流功率、水流功率及有效水流功率）。以流速类指标为驱动因子的成果主要有：Wang等[15]通过不同坡度、流量组合下的水槽输沙试验，认为平均流速与输沙能力呈幂函数关系且响应关系良好，而Zhang等[16]则得出平均流速与输沙能力为线性关系，且相关性随着中值粒径的增大而变弱；在力学类指标研究中，Govers[17]通过5组不同中值粒径加沙试验发现与功率类指标相比，剪切力与输沙能力关系最优；在功率类指标与输沙能力耦合关系的研究中，Ali等[18]通过4组不同中值粒径的水槽动床输沙试验得出单位水流功率与输沙能力关系更为紧密；Wu等[19-20]和栾莉莉等[21]通过水槽加沙试验发现相比剪切力、单位水流功率而言，水流功率与输沙能力关系最优，且其认为水流输沙能力与水流功率1.25次方呈正比关系。可见，坡面水流输沙能力中采用何种水流强度作为驱动因子目前没有定论，且多数学者均选取中值粒径大于0.2 mm的无黏性沙开展研究，而涉及黏性沙的尚不足，黏性泥沙与无黏性泥沙在开动、扬起、止动等动力过程具有较大的差异。

本文将针对于黄土丘陵沟壑区土壤质地，选取中值粒径为0.095和0.04 mm的黏性土，通过定床水槽人工加沙试验，系统研究各水流强度参数与输沙能力间的耦合机制，以期建立适用于黄土丘陵沟壑区的坡面输沙能力计算模型，该研究成果对于土壤侵蚀预报模型的建立和泥沙灾害的防控提供理论依据。

1 材料与方法

1.1 试验土样

试验用土为陕西省神木县沙黄土和安塞黄绵土。神木沙黄土取自中国科学院水利部水土保持研究所安塞侵蚀与环境试验站（110°30′E，38°49′48″N），中值粒径为0.095 mm，土壤颗粒组成见表1。安塞黄绵土取自中国科学院水利部水土保持研究所安塞水土保持综合试验站（109°19′23″E，36°51′30″N），中值粒径为0.04 mm，土壤颗粒组成见表1。

表1 不同试验土壤颗粒机械组成百分比

1.2 试验建立

试验于2017年7月在中国杨凌的黄土高原土壤侵蚀与旱地农业国家重点试验室进行。试验装置主要由试验水槽、恒定水箱、加沙漏斗以及泥沙收集装置组成。其中试验水槽为长4.5 m、宽0.3 m、高0.1 m的可调坡度有机玻璃槽（如图1），通过升降螺栓调整水槽出口高度可使水槽坡度变化。水槽底部铺有凸起高度为0.38 mm的水砂布，用以模拟自然下垫面，使试验时水槽底部粗糙度保持均匀稳定。流量由恒定水箱出口处的放水阀门控制，水流中泥沙由水槽端部0.5 m处的加沙漏斗提供，加沙速率由活动导叶和滚筒转速综合调控。

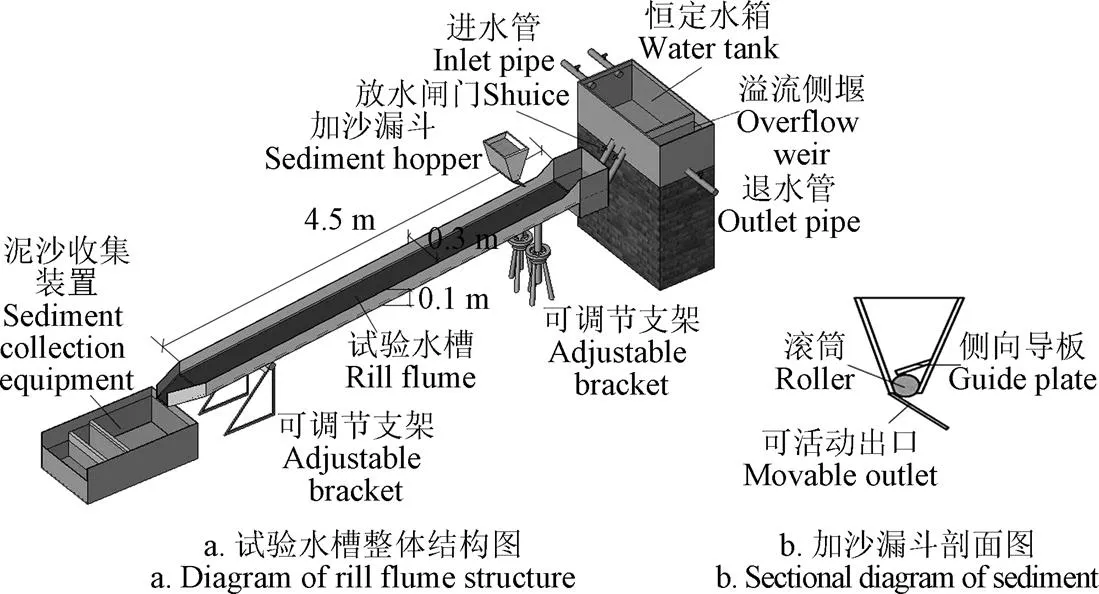
图1 试验水槽布置图

1.3 试验过程

试验中，流量控制采用7个控制阀门的组合实现，流量测量采用称重法，精度为0.001 L/s。在试验加沙之前，将坡度和流量调整到设定值，待流量稳定后，采用SLZ型水位测针测定断面水深，精确至0.01 mm。测试断面布设在距离进口段0+1.0 m、0+2.0 m、0+3.0 m处，每个断面设置3个测点，共设9个测点，取其平均值作为水流的平均水深。表流速采用KMnO4染色法测定，每个测定区间随机测4次，共12次，去掉最大和最小值，取平均值为该断面表层流速，采用Li Gang公式[22]计算流速修正系数得到平均流速。

按照沙玉清教授研究表明，相同水流强度条件下，水流输沙能力呈带状分布规律，即多值对应规律，其带状区域的下边界为不冲输沙能力，上边界为不淤输沙能力[23]。本试验中通过Zhang公式[16]预先推求其输沙量大致范围如公式（1）所示，在该范围前后设计共5组不同的加沙率，随后计算各组中水槽出口挟沙量，认为漏斗加沙量比出口挟沙量略大的临界状态为达到超饱和含沙状态，即不淤输沙能力。若5组均不能达到该要求，则需要再次缩小范围，直至得到该临界值。所测得临界状态为不淤输沙能力值作为本次确定的输沙能力。

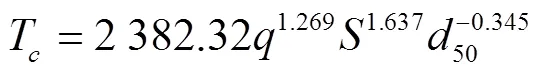
式中T为坡面水流输沙能力，kg/(s·m)；为单宽流量，m2/s；为能坡，%；50为中值粒径，mm。

当测定输沙力时，通过调节电机的转速及漏斗开度调节加沙速率，调节过程中视加沙速率5 min内保持稳定为基本原则。当试验进行时，用铁棒搅拌使得泥沙与水充分混合。待含沙水流流量稳定一段时间后用不同编号的取样桶在水槽出口处取样，取样时间根据流量与容器大小设定，并通过秒表记录，一般不少于30 s。然后把沙样静置沉淀、烘干并称其质量，取沙样质量的平均值作为最后结果。坡面流输沙力计算方法如公式（2）所示。每轮试验结束后，采用烘干法对泥沙样品进行处理，并循环利用。

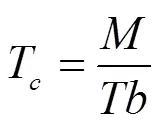
式中为烘干沙样质量，kg；为水槽宽度，m；为取样时间，s。

1.4 数据计算与分析

表征水流强度指标的参数中流速类指标主要有表流速、底流速[24]和平均流速[23]，但由于表流速及底流速在测量上的困难及定义上的不准确性，使得这2个指标未能得到广泛应用，目前，运用更广泛的为平均流速，其计算公式如下

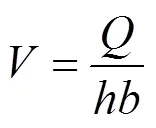
式中为平均流速，m/s；为总流量，m3/s；为水流深度，m。

剪切力作为土壤侵蚀的主要动力，是指坡面流体在运动过程中沿坡度梯度方向所受到的作用力。Yalin[25]方程中的水流剪切力是研究坡面流输沙能力中经常用到的水动力参数，其公式为

式中为水流剪切力，Pa；为水流密度，kg3/m；为重力常数，m2/s。

功率类指标主要包括水流功率、单位水流功率以及有效水流功率。水流功率表示水流在单位时间内做功的多少，体现了一定高度的水流顺坡流动时具有的势能。在水流顺坡流动过程中，势能转换为动能，从而带动坡面泥沙运动，因此，水流功率是计算输沙能力的重要参数。水流功率最初用于明渠流中，Bagnold[26]将坡面流输沙能力的研究重点从水流剪切力转移到能量的消耗速率，即水流功率，其表达式为

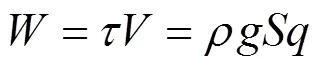
式中为水流功率，W/m2。

单位水流功率被Yang[27]定义为作用于泥沙床面的单位质量水体势能随时间的变化率，即单位质量水体在输送泥沙时所消耗的能量，并建立了单位水流功率与流速和能坡的关系式

=（6）

式中为单位水流功率，m/s。

有效水流功率是Govers[28]基于水流剪切力的概念提出的，可以理解为水流除去内部摩擦切应力损失后的净输出功率。有效水流功率能够反映水流实际输出功率的大小，其值越大，水流的能量越多，带动的坡面泥沙越多，即输沙能力越大。公式如下

式中W为有效水流功率，N1.5/(s1.5m2.17)。

为消除量纲对输沙能力的影响，现将输沙能力及各水流强度指标进行无因次化，其公式如表2。

表2 水流强度指标的无量纲公式

注：γ为泥沙颗粒容重；为水的容重；为泥沙颗粒沉速；为坡降；50为泥沙颗粒中值粒径；V为无量纲平均流速；为无量纲剪切力；W为无量纲水流功率；P为无量纲单位水流功率；W为无量纲有效水流功率；为无量纲输沙能力。下同。

Note :γis the bulk density of sediment particles;is the bulk density of water;is the sedimentation speed of sediment particles;is slope descent;50is sediment median particle size; Vis the non-dimensional mean fiow velocity;is the non-dimensional shear stress; Wis the non-dimensional stream power; Pis the non-dimensional unit stream power;Wis the non-dimensional effective stream power;is the non-dimensional sediment transport capacity. Same as below.

输沙能力的无量纲化形式很多种，主要是因为输沙能力可以分别通过采用泥沙性质有关的物理量和水流条件的物理量来无量纲化，也可以将两者结合来进行无量纲化。黄才安等[29]曾采用以上无量纲化处理后提出一般水流强度指标形式，并建立输沙率公式。本次采用以上公式进行计算，在无量纲化的过程中引入了沉速等泥沙因子，泥沙颗粒中值粒径不同会对各参数造成差异，但是沉速作为静态水中泥沙沉降速度，中值粒径对其影响较小，在本研究中可忽略不计，且输沙能力与各水流强度指标均采用以上公式无量纲化处理，中值粒径对各水流强度指标的影响将随之削弱。

本次试验数据共92组，反映了两组中值粒径（0.095和0.04 mm）在不同坡度、单宽流量组合下的输沙能力。现将全部数据随机分为2组，第一组包括46组数据，用于研究坡面水流输沙能力与各水流强度指标之间的响应关系，并通过回归得出对应的计算公式；另一组包括46组数据用于方程验证，以评估这些方程的适用性。在评价相关公式的适用性时，选用相关系数2和Nash-Sutcliffe系数（N）对公式模拟情况进行校验[30]

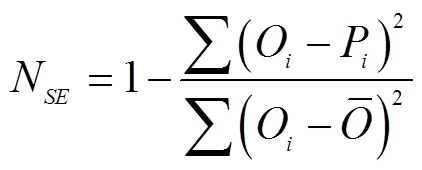
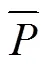
2 结果与分析

2.1 坡度、单宽流量与输沙能力的响应关系

坡度、单宽流量是土壤侵蚀研究中的重要因子，是决定坡面侵蚀程度的主要因素，因此在输沙能力的计算方法中占有重要地位。现绘制出坡度、单宽流量与输沙能力的三维坐标图，如图2a所示，以期分析三者间的响应关系。

由图2a可见输沙能力T整体随着坡度、单宽流量的增长而单调递增，呈幂函数关系，这与Guy等[31]、Zhang等[13]、Wang等[15]的研究结果一致。当单宽流量在0.03～0.17 dm2/s范围内时，T随能坡的变化出现波动状态且在能坡为0.06～0.22时，T亦随单宽流量波动。其波动原因主要包括两方面。一方面当单宽流量、能坡足够小时，含沙水流有滚波产生，波动将对试验观测产生影响；另一方面，泥沙起动及落淤动力条件受到滚波影响，波峰与波谷处泥沙含量分别为超饱和状态与次饱和状态，出口接取该含沙水流时，水流中波峰和波谷的数量会直接影响其泥沙含量（如图3）。以上原因均可能导致输沙能力呈波动状态。在同一单宽流量下，能坡从0.22至0.38，dT/d增大，即T增加幅度更大；在同一能坡下，单宽流量在0.17～0.33 dm2/s内T增长逐渐变快，因此整体考虑T与之间为幂函数增长。另外，采用SPSS分别对输沙能力与单宽流量、能坡进行显著性检验，得出单宽流量（=33.084）比能坡（=24.679）对输沙能力的影响更为显著，采用多元回归分析，并得出三者关系式如下：

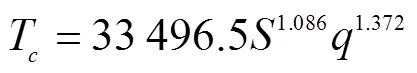
输沙能力与能坡、单宽流量的关系呈幂函数关系，R2=0.965。通过比较公式（10）中坡度与单宽流量的指数发现，能坡的指数1.086比单宽流量的指数1.372小20.85%，与显著性检验结果一致，说明在本研究中单宽流量比能坡对输沙能力影响更为显著。

图3 不同试验工况下的含沙水流现象比较

为了评估公式（10）以及Zhang等[13]、Wu等[19]、Mahmoodabadi等[32]公式对本次研究的适用性，将第二组数据分别带入3个公式校验，绘制实测值与各模拟值关系图如图2b、图4所示，并分析其相关性如表3。

由图2b可以看出本次研究所得公式结果均匀分布在1:1线周围，显然模拟值与实测值拟合较好，仅有个别低含沙量模拟值存在偏差，公式（10）模拟效果很好（2=0.99，N=0.959）；而图4中Zhang公式所得模拟值均较大于实测值，对本研究适用情况一般（2=0.987，N=0.76）；Wu公式以及Mahmoodabadi公式则并不能用于本研究中输沙能力的预测，Wu公式模拟值均小于实测值（2=0.982，N=−0.878），而Mahmoodabadi公式则均大于实测值（2=0.924，N=−3.174）。通过以上分析，本次研究所得公式（10）可作为坡面流输沙能力的预测公式。

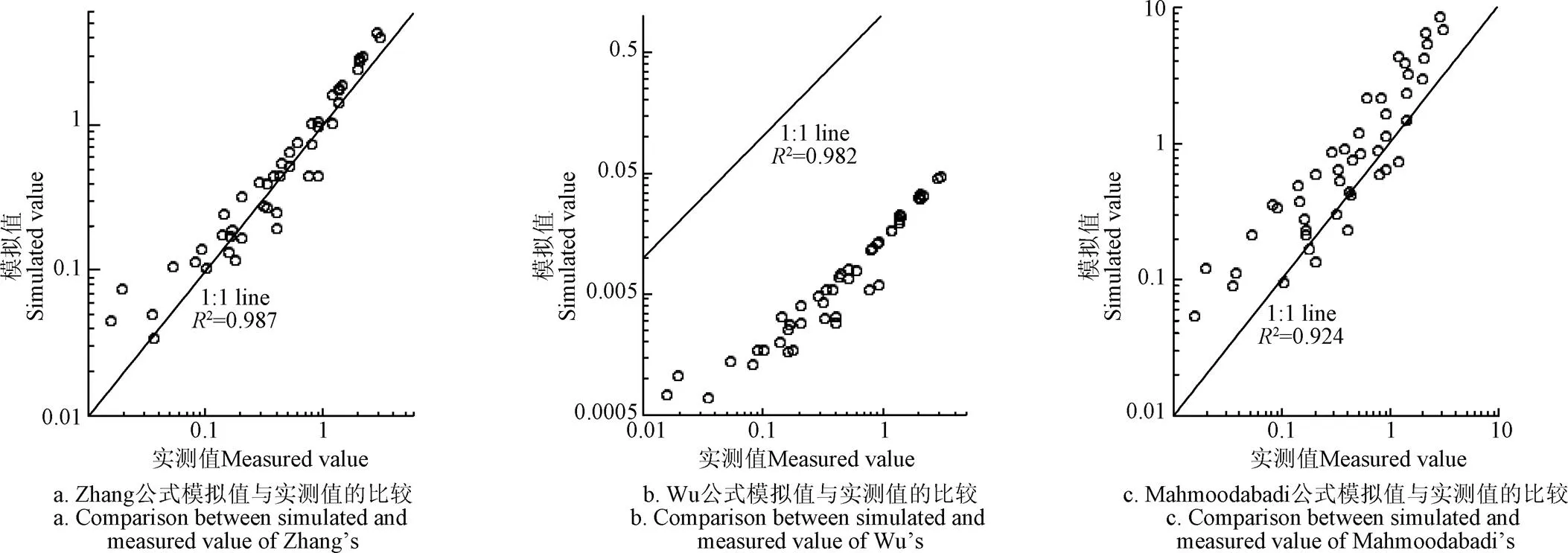
图4 Zhang、Wu、Mahmoodabadi公式模拟值与实测值关系图

表3 各模型关于本研究适用性的比较

2.2 平均流速与输沙能力的响应关系

鉴于坡面水流输沙能力是坡度与单宽流量的函数，可预测平均流速与能坡、单宽流量存在密不可分的关系。现对平均流速、能坡与单宽流量采用多元回归分析，得出三者之间的关系式：

在本次研究中平均流速为能坡、单宽流量的幂函数，现将整体数据无量纲化处理，研究分析无量纲平均流速与无量纲输沙能力之间的关系。图5为Φ与V*幂函数关系及其公式拟合程度。

如图5a所示为无量纲流速V与无量纲输沙能力的关系图，试验点整体呈带状分布，随着V的增加而增加。比较不同粒径之间无量纲流速与输沙能力公式发现，粒径为0.095 mm的沙黄土流速指数为4.643 6，当无量纲流速由4变化到10时，无量纲输沙能力由2增长至145，指数较大，增长较快；粒径为0.04 mm的黄绵土流速指数为1.778 6，当无量纲流速由4变化到10时，无量纲输沙能力由11变化至57，指数较小，增长较慢。究其原因，这可能是由于起动临界条件不同所致，根据shieds曲线可知，粒径小于0.2 mm时，起动流速均随粒径的增大而增大。综合数据分析，对于无量纲流速与坡面流无量纲输沙能力的拟合关系为幂函数关系，关系式如下

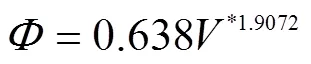
为了验证公式（12）的准确性，采用该公式计算出模拟值，并与研究中的实测值进行对比，采用双对数坐标表示，分析结果如图5b。验证结果进一步说明，该公式所预测的无量纲输沙能力值良好（2=0.947），公式（12）可用于坡面水流输沙能力的预测。

2.3 剪切力与输沙能力的响应关系

从泥沙输移角度考虑，只有当坡面水流冲刷力大于土壤颗粒抗滑力时，坡面才会发生侵蚀，因此，坡面侵蚀输沙与剪切力密不可分。图6为与幂函数关系及其公式拟合程度。

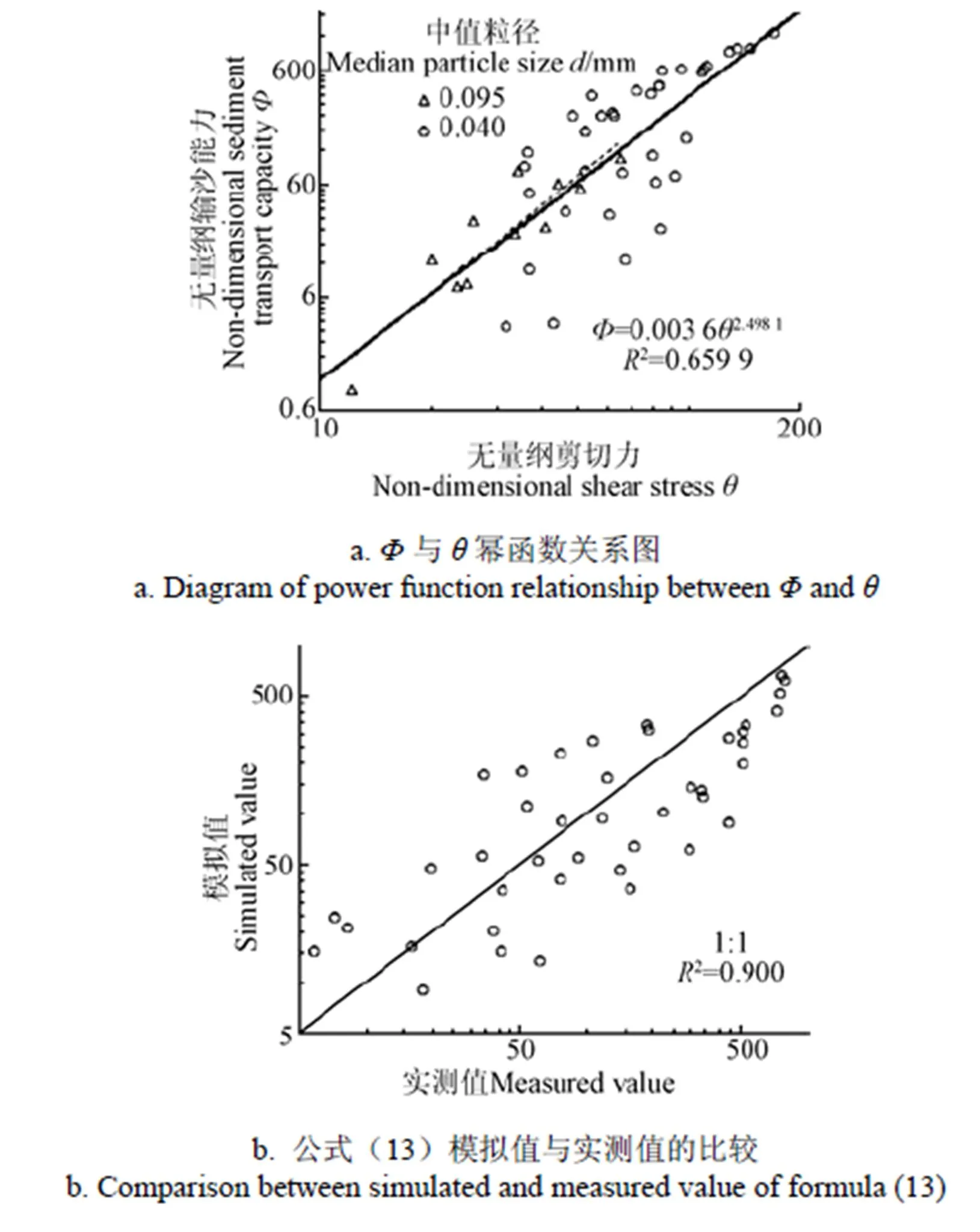
图6 Φ与θ幂函数关系及其公式拟合程度

如图6a所示为无量纲剪切力与无量纲输沙能力双对数关系图，整体呈带状分布，其中中值粒径为0.04 mm的试验数据带状区域较为分散，2种粒径的剪切力指数分别为2.619和2.547，十分接近，可以说明粒径对剪切力与输沙能力关系影响很小。对于黏性土而言，颗粒间相互粘连，受到水流冲刷时成块起动，这使黏性土力学指标对输沙能力的影响较不明显。综合2种粒径发现无量纲剪切力与输沙能力间存在幂函数关系，公式如下

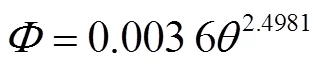
Zhang等[16]对无黏性沙输沙能力研究得出剪切力与输沙能力幂函数指数为2.06～2.32，与本研究黏性土所得2.49相差较小，因此土壤颗粒中值粒径对剪切力指数并不产生影响。为了评价该公式对预测坡面水流输沙能力的准确程度，将数据代入检验。将公式（13）计算所得出的模拟值与实测值用双对数坐标表示如图6b所示，整体预测较好（2=0.900）。剪切力并不适合作为准确预测黏性土输沙能力的指标。

2.4 功率类指标与输沙能力的响应关系

从能量角度而言，坡面水流土壤侵蚀是剪切力做功消耗能量的过程，因此功率类指标与输沙能力的关系极其密切。现分析无量纲单位水流功率、水流功率以及有效水流功率与输沙能力间的响应关系。图7为与P幂函数关系及其公式拟合程度。

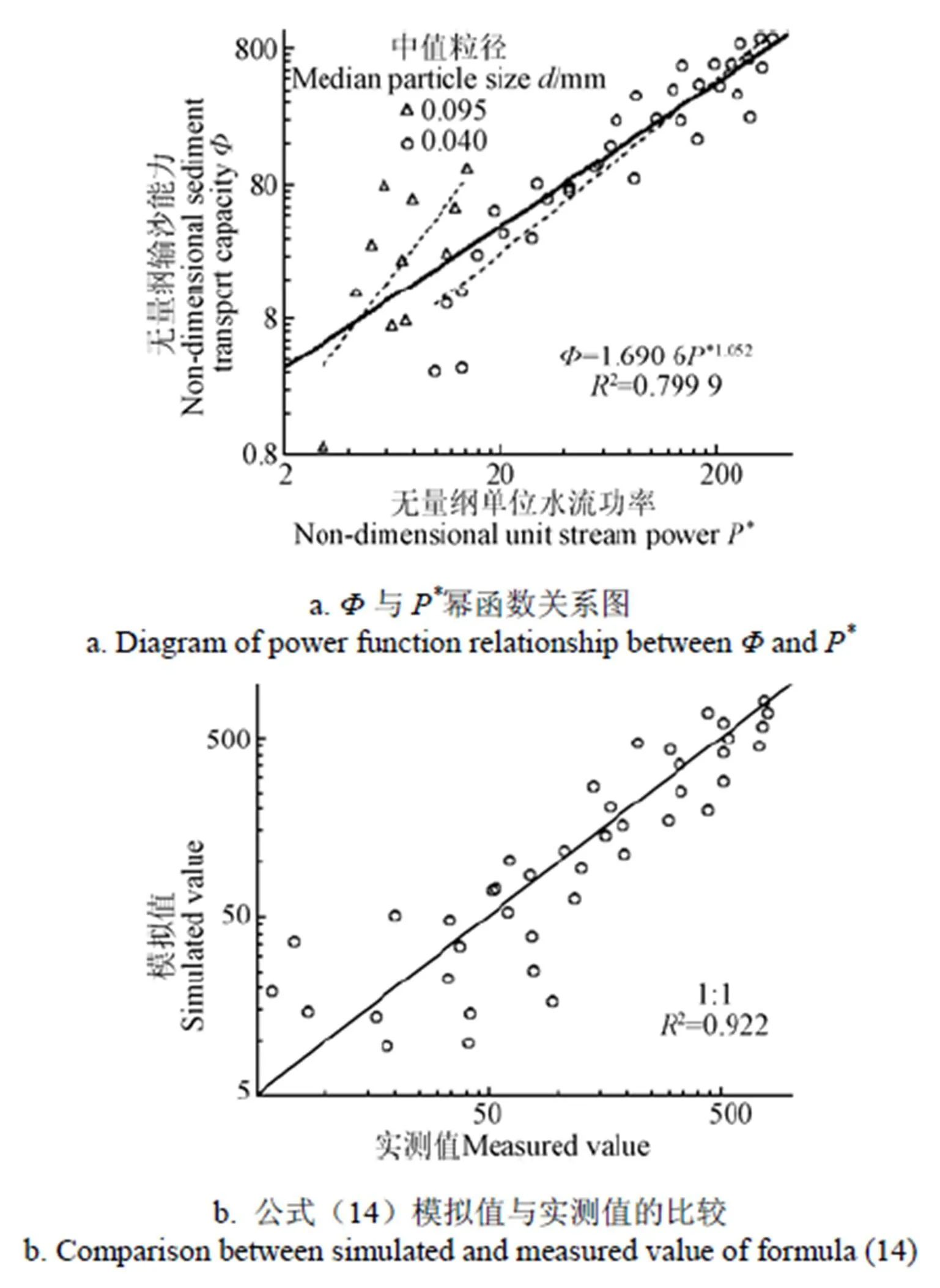
图7 Φ与P*幂函数关系及其公式拟合程度

图7a所示，为无量纲输沙能力与无量纲单位水流功率P双对数关系图，显然图像散点分布较分散，拟合效果并不理想。不同粒径无量纲单位水流功率指数为2.084 1和1.280 5，相差较大，说明指数会受到中值粒径的影响。其关系为幂函数，公式如下

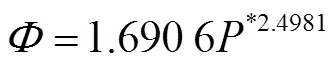
比较不同中值粒径下单位水流功率与输沙能力拟合公式，中值粒径为0.04 mm的黄绵土指数2.0841比Ali等[18]所得指数2.89小27.89%，而中值粒径为0.095 mm指数与其相差更多，这归因于本次研究对象为黏性土，Ali等[18]在研究中采用的是无黏性沙。为验证公式（14）的预测能力，现将计算所得模拟值与实测值用双对数坐标表示如图7b所示，对低含沙量水流预测并不理想（R2=0.922）。因此，在本次研究中不推荐公式（14）作为坡面水流输沙能力的预测公式。图8为Φ与W*幂函数关系及其公式拟合程度。

图8a绘制为无量纲水流功率W与无量纲输沙能力关系图，当水流功率达到一定临界值时，床面泥沙才能开动、扬起，故考虑临界水流功率，并通过实测值线性延展得出其无量纲值近似为36.5。由图8b可见水流功率与输沙能力耦合关系良好，且2种中值粒径下，W-W0指数为1.235 8和1.314 2相接近。综合以上可得公式如下：

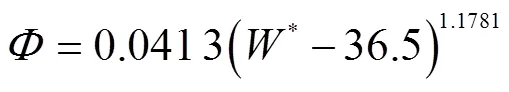
式中0为临界水流功率取为36.5。为了评价公式（15）对坡面水流输沙能力预测的准确性，经数据检验如图8b。显然，公式预测效果很好（2=0.992），只有较小输沙能力中实测值比公式（15）的模拟值稍大，可以用于坡面水流输沙能力的预测计算。

图9为与W幂函数关系及其公式拟合程度。图9a所示，为无量纲输沙能力与无量纲有效水流功率W双对数关系图，显然图像散点分布较均匀。综合认为两者为幂函数关系，公式如下

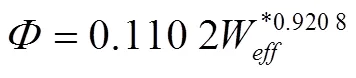
为了评价公式（16）对坡面水流输沙能力预测的准确性，对其检验如图9b，公式（16）预测效果较差（R2=0.971）。

3 讨 论

在本次研究中，发现坡面流输沙能力分别随着坡度、单宽流量的增加而增加，呈幂函数关系增长，且单宽流量较能坡对输沙能力的影响更为显著，这与Meyer[11]、Zhang等[13]、Aziz等[14]研究结果一致。在本次研究中能坡为0.06~0.22、单宽流量为0.03～0.17 dm2/s时，输沙能力会受到滚波影响而出现波动情况。现通过表3对4个公式对比发现Wu等[19]、Mahmoodabadi等[32]所得模型并不适用于本次研究，其中Wu模型坡度范围为10.51%～38.39%，为陡坡试验，且其在试验水槽下游出设计泥沙放样室，试验所测得输沙能力为次饱和状态即不冲输沙能力，而本次试验则是根据漏斗加沙量比出口挟沙量略大确定输沙能力的，为超饱和状态即不淤输沙能力，因此该公式模拟值均比本研究实测值偏小。而Mahmoodabadi模型则是通过对小坡度的无黏性沙研究所得，与本次研究相差极大，这表明关于无黏性沙的土壤侵蚀模型并不适用于黏性土输沙能力的预测。

流速在坡面水流输沙能力的研究中至关重要，通常取决于试验坡度、流量以及河床的形态，其中河床形态决定了流速是否可作为坡面水流输沙能力的预测指标[18,31]。本次研究为了证明流速的影响因素，分析得出平均流速可以表示为坡度、流量的幂函数。无量纲流速与坡面水流输沙能力关系密切，为幂函数关系。但由于流速受到水力学参数（流量、坡度、粗糙度，水深及粒径）和地表条件等多因素影响，致使无量纲流速与输沙能力关系不能达到最佳，且其指数受中值粒径的影响较大。

剪切力是否可以作为坡面水流输沙能力的预测因子，目前尚未定论，Zhang等[13]、Nearing等[7]和Wu等[19]研究表明，剪切力指标与坡面水流输沙能力响应关系良好；但也有Rauws等[33]、Govers等[28]表明剪切力并不能作为输沙能力的预测因子。在本次研究中无量纲剪切力与坡面水流输沙能力响应关系呈带状分布，这是由于土壤颗粒结构所致。根据沙玉清教授研究表明[24]，黏性土颗粒在起动时会先在泥沙表面形成缓和波形，波顶的土粒被水流卷扬而起；而无黏性沙则是逐渐起动，呈沙波起伏前进，受到剪切力影响更大。因此，在黏性土的输沙能力研究中力学指标对输沙能力影响并不显著。

在功率类水流强度指标中，单位水流功率对坡面流输沙能力的预测效果较差，这与Zhang等[13]、Wu等[19]的研究结果相一致。无量纲水流功率、有效水流功率与坡面水流输沙能力的响应关系很理想，考虑临界水流功率的输沙能力计算公式（2=0.950）比有效水流功率（2=0.918 5）效果更好，但有效水流功率仍然是今后研究的范围。本次研究所得出的基于水流功率的坡面水流输沙能力计算方法适用于黏性土输沙能力的预测。

4 结 论

1）坡面水流输沙能力随坡度、单宽流量的增加而增加，整体为幂函数关系，且相比于坡度，单宽流量对输沙能力影响更为显著。

2）在各水流强度指标与坡面流输沙力的响应关系中，无量纲水流功率、无量纲有效水流功率与输沙能力的关系显著；流速受到能坡与单宽流量的影响，与输沙能力关系不佳；剪切力对坡面水流输沙能力的关系取决于土壤颗粒结构；单位水流功率指标则不能用于输沙能力的预测。

3）水流功率与输沙能力关系最优，其中考虑临界水流功率取36.5，无量纲水流功率与坡面水流输沙能力为幂函数关系，且预测精度高达2=0.950，Nash-Sutcliffe系数为0.978。

[1] UNEP. Status of desertification and implementation of the United Nations plan of action to combat desertification[R]. 1992.

[2] 中国科学技术协会. 土壤学学科发展报告[M]. 北京：中国科学技术出版社，2011.

[3] Lal R. Soil erosion impact on agronomic productivity and environment quality[J]. Critical Reviews in Plant Sciences, 1998, 17(4): 319－464.

[4] 朱显谟. 抢救“土壤水库”实为黄土高原生态环境综合治理与可持续发展的关键－四论黄土高原国土整治28字方略[J]. 水土保持学报，2000，14(1)：1－6.

Zhu Xianmo. Saving “Soil Water Reservoir” is a key issue for integrated control of ecological environment and sustainable development on loess plateau-The fourth discussion on “28 words” strategy for land and environment harness on Loess Plateau[J]. Journal of Soil and Water Conservation, 2000, 14(1): 1－6. (in Chinese with English abstract)

[5] 景可，王万忠，郑粉莉. 中国土壤侵蚀与环境[M]. 北京：科学出版社，2005.

[6] Merten G H, Nearing M A, Borges A L O. Effect of sediment load on soil detachment and deposition in rills[J]. Soil Science Society of America Journal, 2001, 65(3): 861－868.

[7] Nearing M A, Forster G R, Lane L J, et al. A process-based soil erosion model for USDA-Water Erosion Prediction Project Technology[J]. Transactions of The American Society of Agricultural Engineers, 1989, 32(5): 1587－1593.

[8] Ritsema C J, Wesseling C G, Roo D A P J. LISEM: A single-event physically based hydrological and soil erosion model for drainage basins; I: Theory, input and output[J]. Hydrological Processes, 1996, 10(8): 1107－1117.

[9] Julien P Y, Simons D B. Sediment transport capacity of overland flow[J]. Transactions of the ASAE-American Society of Agricultural Engineers (USA), 1985, 28(28): 755－762.

[10] Prosser, I P, and P Rustomji. Sediment transport capacity relations for overland flow[J]. Progress in Physical Geography: 2000, 24(2): 179－193.

[11] Meyer L D. Transport of sand-sized sdiment along crop-row furrows[J]. Trans Asae, 1983, 26(1):106－111.

[12] 雷廷武，张晴雯，赵军，等. 细沟侵蚀动力过程输沙能力试验研究[J]. 土壤学报，2002，39(4)：476－482.

Lei Tingwu, Zhang Qingwen, Zhao Jun, et al. Experimental study on sand transport capacity of rill erosion process[J]. Chinese Journal of Soil Science, 2002, 39(4): 476－482. (in Chinese with English abstract)

[13] Zhang G H, Liu Y M, Han Y F, et al. Sediment transport and soil detachment on steep slopes: I. Transport capacity estimation[J]. Soil Science Society of America Journal: 2009, 73(4): 1291－1297.

[14] Aziz N, Scott D. Experiments on sediment transport in shallow flows in high gradient channels[J]. International Association of Scientific Hydrology Bulletin, 1989, 34(4):465－478.

[15] Wang Z, Yang X, Liu J, et al. Sediment transport capacity and its response to hydraulic parameters in experimental rill flow on steep slope[J]. Journal of Soil & Water Conservation, 2015, 70(1): 36－44.

[16] Zhang G H, Wang L L, Tang K M, et al. Effects of sediment size on transport capacity of overland flow on steep slopes[J]. Hydrological Sciences Journal, 2011, 56(7): 1289－1299.

[17] Govers G. Empirical relationships for the transport capacity of overland flow [J]. IAHS Press: 1990(3): 45－63.

[18] Ali M, Seeger M, Sterk G, et al. A unit stream power based sediment transport function for overland flow[J]. Catena, 2013, 101(3): 197－204.

[19] Wu B, Wang Z, Shen N, et al. Modelling sediment transport capacity of rill flow for loess sediments on steep slopes[J]. Catena, 2016, 147:453－462.

[20] Wu B, Wang Z, Zhang Q. Modelling sheet erosion on steep slopes in the loess region of China[J]. Journal of Hydrology, 2017,553: 549－558.

[21] 栾莉莉，张光辉，王莉莉，等. 基于水流功率的坡面流挟沙力模拟[J]. 泥沙研究，2016，2：61－67.

Luan Lili, Zhang Guanghui, Wang Lili, et al. Study on sediment transport capacity of overland flow based on stream power[J]. Journal of Sediment Research, 2016, 2: 61－67. (in Chinese with English abstract)

[22] Li G, Abrahams A D, Atkinson J F. Correction factors in the determination of mean velocity of overland flow[J]. Earth Surface Processes & Landforms, 2015, 21(6): 509－515.

[23] 沙玉清. 泥沙运动学引论[M]. 北京：中国工业出版社，1965.

[24] Willis J C, Coleman N L, Ellis W M. Laboratory study of Transport of fine sand[J]. American Society of Civil Engineers, 1972, 100: 317－318.

[25] Yalin M S. An expression for bed-load transportation[J]. J.hydraul.div.asce, 1963, 89: 221－250.

[26] Bagnold R A. An approach to the sediment transport problem from general physics[J]. Us Geol.surv.prof.paper, 1966, 422-i: 231－291.

[27] Yang C T. Unit stream power and sediment transport[J]. Journal of the Hydraulics Division, 1972, 98: 1805－1826.

[28] Govers G. Evaluation of Transporting Capacity Formulae for Overland Flow[M]//Overland Flow, Hydraulics and Erosion Mechanics,1992: 243－273.

[29] 黄才安，奚斌. 水流强度指标与推移质输沙率[J]. 扬州大学学报：自然科学版，1999(1)：68－73.

Huang Caian, Xi Bin. Measures of flow intensity and bed load transport rate[J]. Journal of Yangzhou University: Natural Science Edition, 1999(1): 68－73. (in Chinese with English abstract)

[30] Nash J E, Sutcliffe J V. River flow forecasting through conceptual models part I-A discussion of principles[J]. Journal of Hydrology, 1970, 10(3): 282－290.

[31] Guy B T, Dickinson W T, Rudra R P, et al. Hydraulics of sediment-laden sheetflow and the influence of simulated rainfall[J]. Earth Surf Proc Land, 1990, 15: 101－118.

[32] Mahmoodabadi M, Ghadiri H, Rose C, et al. Evaluation of GUEST and WEPP with a new approach for the determination of sediment transport capacity[J]. Journal of Hydrology, 2014, 513(513): 413－421.

[33] Govers G, Rauws G. Transporting capacity of overland flow on plane and on irregular beds[J]. Earth Surface Processes & Landforms, 1986, 11(5): 515－524.

Overland flow sediment transport capacity calculation method based on non-dimensional flow intensity index

Gao Chenye1, Zhang Kuandi1,2※, Yang Mingyi2

(1. Key Laboratory of Agricultural Soil and Water Engineering of Ministry of Education in Arid Areas, Northwest A&F University, Yangling, 712100, China; 2. State Key Laboratory of Soil Erosion and Dryland Farming on the Loess Plateau, Northwest A&F University, Yangling, 712100, China)

Overland flow sediment transport capacity is one of the important parameters of soil erosion model, and it is also a basis for accurate prediction of soil erosion. In this paper, the typical loess with two different median diameters (median size50=0.095 mm,50=0.04 mm) in the sandy and coarse sand area was used in the simulation experiment of sediment transport capacity in the sink. The slope gradient range was from 7% to 38.4% and the unit discharge range was 0.000 14-0.005 26 m2/s. After unqualified analysis, the coupling relationship between the sediment transport capacity and slope gradient, unit discharge and the flow intensity indicators (the mean flow velocity, shear stress, unit stream power, stream power, effective stream power) were analyzed. The results showed that the sediment transport capacity exhibited an increasing trend with increased slope gradient and unit discharge, and the sediment transport capacity had a power function relation with the slope gradient and the unit discharge (2=0.955). The index of slope gradient was 1.086 and the index of unit discharge was 1.372. So, the unit discharge had more significant impact on sediment transport capacity than slope gradient. Compared with Zhang’s, Wu’s, and Mahoodabadi’s models, Zhang’s model had a basic trial of this research , and the results of Bing Wu's model were all less than the measured values in this study, while Mahmoodabadi’s model was the opposite. The mean flow velocity could be predicted by a power function of slope and flow, the relation between sediment transport capacity and mean velocity was also a power function relation ,with an index of 1.9072 (2=0.857 3,Nash-Sutcliffe coefficientN=0.879 5). Because the mean flow velocity was affected by many factors such as hydraulic parameters and surface conditions, the relationship between mean flow velocity and sediment transport capacity could not be optimized. For example, the index was significantly (<0.05) affected by the median diameter of sediments. Shear stress could be used to predict the sediment transport capacity through power function relations and the index was 2.498 1 (2=0.900,N=0.756 1), which was not closely related to the influence of soil particle viscosity. The stream power and effective stream power were better predictors than the shear stress, considering the critical stream power0=36.5. The power function relation of steam power and sediment transport capacity was the best (2=0.950,N=0.978), with an index of 0.920 8. Although the relationship between effective flow power and sediment transport capacity was not optimal, it was still a content of further research. The unit stream power prediction model got poor results for sediment transport capacity (2=0.799 9, N=0.839 6), which was consistent with the results of Zhang’s, Bing Wu’s and others’ studies. So, the unit stream power could not be used as a flow intensity to predict the sediment transport capacity. Based on the dimensionless sediment transport capacity, the formula for calculating the flow capacity of the slope was presented. This study of the sediment transport capacity in the Loess Hilly Gully Area provided a new method for the soil erosion prediction model. It is of great scientific significance to predict slope erosion and to reveal the sediment transport mechanism of slope.

soils; erosion; runoff; overland flow; sediment transport capacity; flow intensity indicators; stream power

10.11975/j.issn.1002-6819.2018.17.018

S157.1

A

1002-6819(2018)-17-0134-09

2018-04-23

2018-07-08

国家自然科学基金资助项目（51579214）；中央高校基本科研业务费（2452017321）；杨凌示范区科技计划项目（2017NY-03）；陕西省博士后配套基金

高晨烨，博士生，主要从事水土保持及坡面水流方面的研究。Email：gaochenye5023@126.com

张宽地，博士，博士生导师，主要从事水工水力学及坡面水流的研究。Email：zhangkuandi428@126.com

高晨烨，张宽地，杨明义. 基于无量纲水流强度指标的坡面流输沙能力计算方法[J]. 农业工程学报，2018，34(17)：134－142. doi：10.11975/j.issn.1002-6819.2018.17.018 http://www.tcsae.org

Gao Chenye, Zhang Kuandi, Yang Mingyi. Overland flow sediment transport capacity calculation method based on non-dimensional flow intensity index[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(17): 134－142. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.17.018 http://www.tcsae.org