“圆的切线方程”教学节录及反思

一、教学节录

1.在问题求解中培养思维能力。

师：请大家证明下列例题：已知圆C的方程是 x2＋y2＝r2，求证：经过圆 C 上一点 M（x0，y0）的切线方程是x0x＋y0y＝r2。（苏教版高中数学必修2第117页习题第11题）

（给学生思考的时间，先由学生独立思考，再相互交流。）

师：请大家思考一下，这位同学的证明是否正确？

生2：我认为他的证明不够严谨，对y0是否为零没有进行分类讨论。他证明的只是y0≠0时的结论，还要考虑到当y0＝0时情形：当y0＝0 时，x0＝r或 x0＝－r。当 x0＝r时，切线方程为 x＝r，满足方程 x0x＋y0y＝r2；同样地，当 x0＝－r时，切线方程也满足这个方程。

师：那么，我有一个疑问，大家都用这种方法来证明的吗？

生3：我是用向量来证明的。我觉得利用向量解决两条直线的垂直关系更加简便。因为可以通过向量的点乘积为零，来回避讨论直线l的率中的分母y0为零的情形。证明方法如下：设P（x，y）是切线上的任意一点，则OM⊥MP，即（x0，y0）·（x－x0，y－y0）＝0，化简，得x0x＋y0y＝r2。所以，点 M（x0，y0）的切线方程是x0x＋y0y＝r2。

师：他说得很好！不仅用向量方法解决了问题，还说明了为什么利用向量来解决问题。今后，在解决直线垂直关系的问题时，大家应当考虑利用向量这一工具来解决，避免不必要的讨论。

2.在解题反思中自主提出问题。

师：大家刚才很好地证明了这个问题，受这个问题启发，你还能提出哪些问题？

（在学生经历思考提出问题的基础上，对同类问题进行整理，得到了以下5个探究问题。）

［探究 1］已知点 M（x0，y0）是圆 C：（x－a）2＋（y－b）2＝r2上一点，求经过点M的圆C的切线方程。

［探究 2］已知点 M（x0，y0）是圆 C：x2＋y2＝r2外一点，求方程x0x＋y0y＝r2所表示的几何意义。

［探究 3］已知点 M（x0，y0）是 C：x2＋y2＝r2内一点，求方程x0x＋y0y＝r2所表示的几何意义。

［探究 4］已知点 M（x0，y0）是圆 C：（x－a）2＋（y－b）2＝r2外一点，求方程（x－a）（x0－a）＋（y－b）（y0－a）＝r2所表示的几何意义。

［探究 5］已知点 M（x0，y0）是圆 C：（x－a）2＋（y－b）2＝r2内一点，求方程（x－a）（x0－a）＋（y－b）（y0－a）＝r2所表示的几何意义。

3.在探究活动中发展创造潜能。

师：我们下面来解决大家所提出的问题。首先，探究1大家会解决吗？

生4：可以用类似于解决前面例1的方法。

师：对的！下面请同学们重点思考探究2。请大家先独立思考，然后再相互交流。

（让学生开展自主探究活动，然后再在相应的小组内进行交流，最后请学生在班级进行交流。）

生 5：我们发现，当点 M（x0，y0）是圆 C：x2＋y2＝r2外一点时，由点M能够向圆C引两条直线 MA，MB（A，B 为切点），方程 x0x＋y0y＝r2就表示直线AB。

师：是这样吗？你是怎样得到的呢？

［证法 1］生 6：如图 1，设 A（x1，y1），B（x2，y2），由例题可知，直线 AM：x1x＋y1y＝r2，直线BM：x2x＋y2y＝r2，因为点 M（x0，y0）都在两直线AM 和 BM 上，所以 x1x0＋y1y0＝r2①；x2x0＋y2y0＝r2②。由方程①、②分别可知，点A，B在直线x0x＋y0y＝r2上。又因为两点确定一条直线，所以直线 AB：x0x＋y0y＝r2。

师：很好！这位同学从已有的结论出发，经过严格的推理论证，得到了结论。我们在解决数学问题时，要善于从已有的结论出发，去解决新的问题。

师：还有其他不同的证明方法吗？

（在随后的课堂交流环节，其他学生又给出了如下4种证明方法）

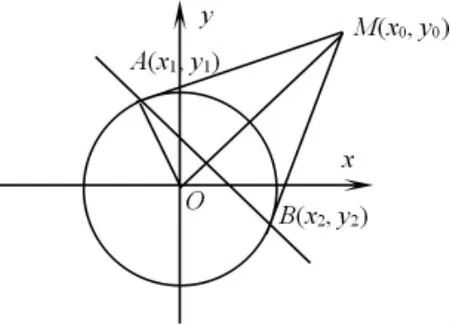
图1

［证法 2］如图 1，连接 OA，OM，AM，设 A（x1，y1）。因为 OM⊥AB，所以为直线AB的法向量，于是可设直线AB：x0x＋y0y＋c＝0 ①。因为点A在直线AB上，所以x0x1＋y0y1＋c＝0 ②。又由AM是圆C在点A处的切线，得 OA⊥AM，所以 OA2＋AM2＝OM2，即 x12＋y12＋（x0－x1）2＋（y0－y1）2＝x02＋y02，即 x0x1＋y0y1=x12＋y12，又 x12＋y12＝r2，所以 x0x1＋y0y1=r2③。把③代入②，得 c＝－r2，再将上式代入①，得直线AB：x0x＋y0y＝r2。

［证法 3］设 A（x1，y1）。连接 OM，以 O 为圆心、OM为半径作圆，则M点在该圆上，以M点为切点作该圆的切线l，则切线l：x0x＋y0y＝OM2。因为 OM⊥AB 且 OM⊥l，所以，AB∥l，于是可设直线 AB：x0x＋y0y＋c＝0，因为点 A 在直线AB 上，所以 x0x1＋y0y1＋c＝0 ①。

因为直线 AM：x1x＋y1y＝r2，且点 M 在直线AM 上，所以 x1x0＋y1y0＝r2②。

由①②可得 c＝－r2，所以直线 AB：x0x＋y0y＝r2。

［证法 4］如图 2，连接 OA，OM，AM，AB，在直线AB上任取一点 Q（x，y），连OQ。设AB 交OM于点T。因为OM⊥AB于点T，所以由射影定理，得又因为由①②可知，直线AB：x0x＋y0y＝r2。

［证法 5］如图 2，设 A（x1，y1）。连接 OA，OM，AM。在直线 AB 上任取一点 Q（x，y），连OQ。因为OM⊥AB，所以即（x－x1，y－y1）·（x0，y0）＝x0x-x0x1+y0y-y0y1＝0，所以 x0x＋y0y＝x0x1＋y0y1①。已知直线 AM：x1x＋y1y＝r2，且点M在直线AM上，所以x1x0＋y1y0＝r2②。由①②可得，直线 AB：x0x＋y0y＝r2。

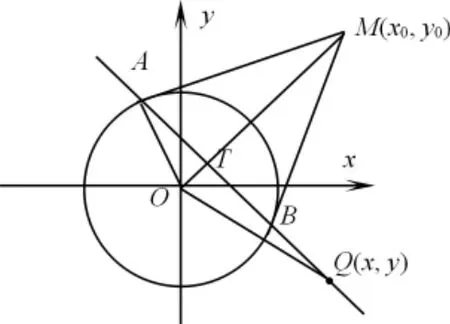
图2

师：大家表现得很棒！分别从不同的角度给出了上面5种不同的证法，很有创造性。

4.在课后探究中形成探究意识。

师：这一节课，同学们不仅解决了教材上已有的习题（例题），还从这个问题出发，提出了新的问题，并且非常成功地完成了探究2，请大家课后继续完成其他的几个探究。

二、教学反思

1.给学生发现问题、提出问题的机会。

发现并提出有意义的数学问题，既是开展数学探究活动的前提，也是培养学生创新精神的关键。本节课，在完成例题之后，让学生从已有的问题出发，提出新的问题，学生从不同的角度（圆的方程不同形式、定点M相对于已知圆的不同位置），提出了5个有价值的探究主题。如果教师不给学生机会，将会很难预料到学生会有这样的能力。因此，在教学中，一定要给学生发现问题、提出问题的机会，培养他们的质疑精神。

2.让学生在探究活动中形成探究意识。

本节课的每一个教学环节，都坚持让学生开展探究，让学生运用已有的知识和方法解决问题。首先，让学生解决例题；在完成例题之后，让学生去发现问题、提出问题，确立新的探究主题；在此之后，又确立新的探究主题（探究2），让学生开展探究活动，学生从不同的角度对问题展开探究，得到了5种证明方法。通过探究活动，不仅充分调动了学生主动运用已有的知识和方法解决新的问题的积极性，而且还培养了学生灵活地运用知识、选择合理的方法解决问题的能力，在解决问题的同时，培养了学生的探究能力与创新意识；最后，还将剩余的几个探究主题作为课后作业，让学生开展探究。通过这样一系列的教学设计，在培养学生的探究能力的同时，培养学生的探究意识，形成良好的探究习惯。

3.使学生通过探究从整体上理解数学。

本节课，由教材的一道习题（例题）出发，通过这一系列的数学探究活动，让学生对圆的切线有了全面而又深刻的认识。需要说明的是：在课后作业环节，对于探究3，学生们不仅基本上得到并证明了“直线x0x＋y0y＝r2与圆相离”这一结论，而且，还有将近三分之一的学生得到并证明了“圆的半径r是线段OM的长与O到l距离的等比中项”这一结论；此外，在随后学习圆锥曲线与直线位置关系时，还可以让学生开展类似的数学探究活动。因此，通过这样一系列的数学探究活动，能够帮助学生从整体上理解数学，形成完整的知识结构，而不是“碎片化”的知识。