相对性原理与时空线性变换

戴又善

(1浙江大学城市学院， 浙江 杭州 310015; 2浙江大学 物理系， 浙江 杭州 310027)

0 引言

在推导惯性系的时空变换公式时,许多相对论教科书和文献往往会事先假设惯性系的时空变换是线性变换。惯性系的时空线性变换特性一方面是与实验结果相符合,另一方面也可以依据惯性系所具有的一些特性来予以理论证明,因此通常认为其并不属于一个额外的理论假设。对此在国内外的不同文献中都有过各种讨论[1-6],当然在一些简明的教科书中常常会省略其证明或者只给出并不严密的证明,这从教学上来讲也是允许的,因为将惯性系的时空线性变换作为一个假设来处理在教学上对于初学者能够带来推导简明的优点,但是要更深入的理解相对论,则需要真正搞清楚为什么惯性系的时空变换是线性变换。

首先对于什么是惯性系,狭义相对论本身并没有给出明确的定义,而是借用了牛顿惯性定律来定义。另外惯性系应该满足狭义相对性原理(以下简称为相对性原理),相对性原理通常的表述为:一切物理规律在所有惯性系中都是等价(平权)的,其核心是所有惯性系在物理上的等价不可区分性,即没有一个惯性系具有特殊地位。在有的证明推导中虽然表面看只用了牛顿惯性定律[6],实际上还是隐含地利用了相对性原理,因为相对性原理要求牛顿惯性定律在所有惯性系中都成立(力学相对性原理)。

满足牛顿惯性定律的参考系是否就一定为惯性系,就一定会满足时空线性变换,事实上并不如此。我们已经知道满足时空分式线性变换的参考系同样可以满足牛顿惯性定律[7],它是弯曲的de Sitter时空的爱因斯坦场方程的真空解,同样具有球对称的时空各向同性的特性,而当其球半径参量趋于无穷大时则回到了平直的闵氏时空,同时分式线性变换也回到了线性变换[8]。因此惯性系的时空线性变换特性严格来说需要无穷大的时空。

惯性系具有时空的均匀性和各向同性,均匀性是指时空的不同“点”是等价的,各向同性是指时空的不同“方向”是等价的, “方向”至少需要由两个“点”的连线所确定。因此均匀性和各向同性是两个不同的概念。值得指出的是de Sitter时空度规虽然与时空坐标有关,但是de Sitter时空的真空解在其坐标原点同样也具有各向同性,而de Sitter时空并不具有平移不变性。另外需要说明的是,通常均匀性和各向同性中的“性”是指性质或特性,因此严格来说需要予以具体的指明,例如对于一块物质材料,其均匀性可以是均匀的颜色、均匀的密度、均匀的温度、均匀的电特性、均匀的磁特性等等。而对于相对论的讨论来说,均匀的时空是指任何的时空点在物理上都是等价的,即具有时空平移不变性。各向同性则是指空间任何方向上都是等价的,即具有空间转动不变性。惯性系的时空特征是在任何方向上的时空平移不变性,因此既要求有无穷大的时空,也包含了时空的均匀性和各向同性。换言之,(任何方向上的)“时空平移不变性”与“时空的均匀性和各向同性”是互相等价的。但由于时空的均匀性和物质的均匀性常常容易被混淆,另外时空本身的各向同性与所选参考系是否各向同性也容易混淆(如时空本身是各向同性的,但所选非惯性系可以不是各向同性),因此为了更加明确和简捷，本文将采用时空平移不变性来讨论。在本文中给予惯性系的定义是具有任何方向上的时空平移不变性,显然这也符合相对性原理对惯性系的等价性要求。

本文将依据相对性原理(其核心是所有惯性系的等价性),利用时空平移不变性来证明惯性系的时空变换必须为线性变换,并进而推导出惯性系时空变换的广义洛伦兹变换公式。

1 惯性系的时空线性变换

由于惯性系在任何方向都具有时空平移不变性，因此为不失一般性可以讨论两个沿X方向相对运动的惯性系，设惯性系S′(x′,t′)相对于惯性系S(x,t)沿X方向以平动速度V0运动，见图1。

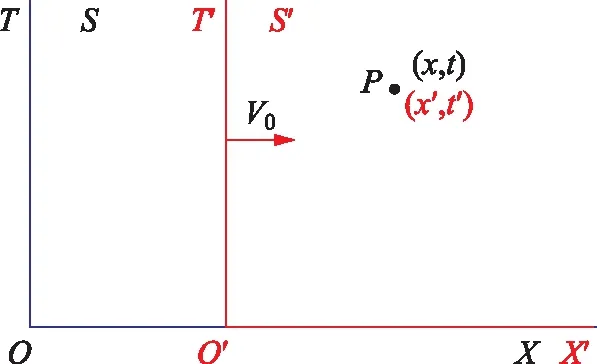
图1 沿X方向相对运动的两个惯性系

惯性系之间的整体相对运动速度V0是与时空坐标无关的常量，这显然是惯性系都具有时空平移不变性的结果。相应的时空变换关系可以最一般性地写为

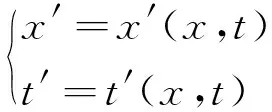
(1)

其中x′(x,t)和t′(x,t)是两个待定函数，对上式微分可得

(2)

由此可求得速度变换关系为

(3)

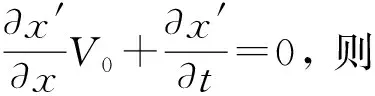
(4)

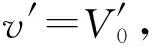
(5)

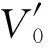
(6)

(7)

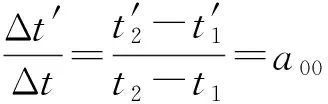
(8)

即有

(9)

a11为常量，反映了空间平移不变性；a00为常量反映了时间平移不变性。对于相对论来讲时空的平移不变性是不独立的,由空间平移不变性可以推出时间平移不变性,反之亦然。则式(6)可改写为(其中a11和a00都为常量)

(10)

(11)

另一方面，设x=x(x′,t′),t=t(x′,t′),依据相对性原理,所有的惯性系都具有时空平移不变性,由同样的讨论,类似于式(6)同样应有

(12)

(13)

比较式(13)和式(11)可得

(14)

(15)

由式(14)还可得关系式

(16)

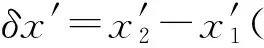
(17)

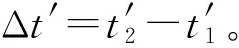
(18)

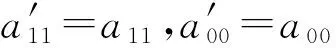
(19)

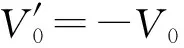
(20)

上式给出了a01与a11的具体关系,由于a11是常量,因此a01显然也是与时空坐标无关的常量,则式(15)可改写为

(21)

对上式积分后,即可得到惯性系的时空线性变换公式(取积分常数都为零的齐次式)

(22)

其中还包含了一个待定常量a11。当取a11=1时就回到了伽利略变换

(23)

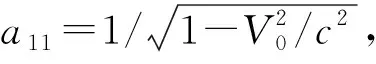
(24)

2 同时的相对性

空间和时间是基本的物理量，最基本的空间间隔测量可由静长(本征长度)来定义，最基本的时间间隔测量可由静止时钟记录的固有时(本征时间)来定义，并由此可定义速度这一导出物理量，即静长为l0的杆运动时，其两端通过某静止时钟的固有时间隔为τ0，则定义该杆的匀速运动速度为v=l0/τ0。这些长度、时间和速度的最基本定义都与“对钟”过程无关。与“对钟”相关的是静止在不同地点时钟的“同时性”定义，要完成同一参考系中的“对钟”校准过程，理论上只需要在两个静止时钟的距离中点发送某种“各向同性”的信号(由于惯性系的时空均匀性和各向同性，这种“各向同性”的信号是存在的)，就可以将两个时钟校准，这一校准过程并不需要事先知道信号的运动速度。而利用这两个已经校准好的时钟就可以测量出该信号在该惯性系的运动速度，利用该各向同性的信号原则上就可以校准该惯性系的所有时钟(在一定实验精度下)，从而建立起该惯性系的时间体系[9]。

对于不同惯性系各自建立的时间体系之间则是无法通过“对钟”过程来校准的，这称为“同时的相对性”。“同时的相对性”既可以利用光信号和光速不变假设来直观说明，也可以用惯性系的时空线性变换公式来予以证明。对于发生在不同时空点的任意两个事件1(x1,t1)和事件2(x2,t2)，由于惯性系的时空变换是线性变换，因此时空间隔的变换同样为线性变换，即

(25)

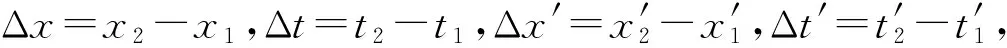
(26)

对于伽利略变换,a11=1,显然有Δt′=Δt=0,即同时事件在所有惯性系中都为同时。对于伽利略变换,同时性是绝对的,与参考系的选择无关。而对于非伽利略的任何线性变换,a11≠1,则有Δt′≠0,即S系中的异地同时事件在S′系中必为不同时事件，同时性将依赖于参考系的选择，称为“同时的相对性”。因此“同时的相对性”并不是唯一依赖于光速不变假设和洛伦兹变换[10],对于惯性系的时空线性变换,只要是非伽利略变换都具有“同时的相对性”。

3 极限速度与广义洛伦兹变换

惯性系的速度变换关系式(3)可改写为

(27)

直接求解其逆变换关系为

(28)

定义无量纲速度

(29)

则有

(30)

对上式u′=u′(u)和u=u(u′)分别求导可得

(31)

由此说明了u′=u′(u)和u=u(u′)都是单调递增的函数[11]。

因为式(30)中的分母为零将使得u′=u′(u)和u=u(u′)的取值分别为无穷大,并且是函数u′=u′(u)和u=u(u′)的不连续奇点,因此物理上要求式(30)中的分母不能为零,则有限制条件

(32)

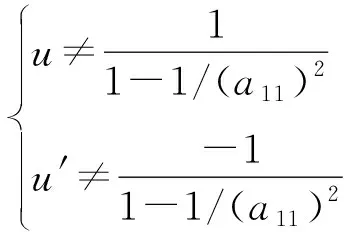
(33)

(34)

从以上两式都可化为

(35)

(36)

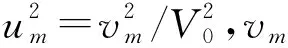
如果在参考系变换下存在一个不变的速度v0,则应该满足v→v0,v′→v0,由速度变换式(27)则有

(37)

由此可解得

(38)

与式(36)相比较,由此证明了此不变速度即为极限速度v0=vm。

将式(36)代入式(22)则可最后确定惯性系的时空线性变换为广义洛伦兹变换[11-12]

(39)

其中的vm既是极限速度又是不变速度。如果实验上确定了光速严格等于极限速度,即取vm=c,则回到了通常的洛伦兹变换公式。

与通常利用光速不变假设来推导洛伦兹变换的最主要不同之处为,本文是依据相对性原理证明了普适极限速度vm的存在,我们并未要求一定存在以极限速度运动的粒子(即静质量为零的粒子),也就是说只要求粒子运动能够无限趋近极限速度vm而并不一定需要有粒子运动实际达到极限速度。另外我们并未在理论上引进额外假设来事先限定极限速度,而是可以依据实验结果来确定极限速度的取值,这样就使得相对论具有了更广的适用范围[13]。需要强调的是广义洛伦兹变换中的极限速度需要通过实验来确定,可以通过各种不同粒子的实验测量来确定极限速度的取值,而其中通过测量光速来确定极限速度vm≈c在目前则是实验上一个精度较高的取值,这也与传统相对论通过理论上的光速不变假设来引进极限速度相自洽。换言之,传统相对论取vm=c是本文给出的广义洛伦兹变换的一个特例。虽然在理论上极限速度vm允许具有比光速c更广的取值范围,而在目前的测量结果和实验精度下两者的取值是相一致的。

4 小结和讨论

(1) 本文依据相对性原理(即所有惯性系的等价性)以及利用惯性系的时空平移不变性证明了惯性系的时空变换必须为线性变换。在文献[6]中利用了牛顿惯性定律来推导惯性系的时空线性变换特性,并得出结论说牛顿惯性定律是推导惯性系时空线性变换缺一不可的必要条件,这一结论并不准确。牛顿惯性定律可以是推导惯性系时空线性变换的充分条件,但并非必要条件。利用惯性定律实际上就隐含着已经利用了相对性原理,因为隐含着牛顿惯性定律对所有惯性系都适用。所以相对性原理才是推导惯性系时空线性变换的真正必要条件。

(2) 本文同时证明了空间平移不变性和时间平移不变性两者并不独立,由空间平移不变性可以推出时间平移不变性,反之亦然。这是因为在相对论中时空是统一的,空间和时间之间互相有关联。我们知道动量守恒根源于空间平移不变性,而能量守恒根源于时间平移不变性,因此在相对论中动量守恒定律与能量守恒定律并不是互相独立的定律[14]。但是需要注意的是,对于经典的伽利略变换,虽然也是线性变换,也满足力学相对性原理,但由于经典力学中时间和空间是独立的,另外经典的能量虽然包含动能但并不包含静能,因此在经典力学中动量守恒定律与能量守恒定律是两条独立的定律[15]。

(4) 本文利用惯性系的时空线性变换公式证明了“同时的相对性”,除了伽利略变换外的任何时空线性变换都可以用来说明“同时的相对性”,即在一个惯性系中的两个异地同时事件,在另一个惯性系中一定不同时。需要特别指出的是, “同时的相对性”并不需要事先确定时空线性变换为洛伦兹变换,本文讨论中也没有引进光速不变假设,“同时的相对性”是相对论时空本身具有的一种基本特性,并不依赖于某种外在特殊粒子的特性。

(5) 本文给出了一种完全利用相对性原理来推导出惯性系广义洛伦兹变换的方法。首先依据相对性原理证明了惯性系的时空变换必须为线性变换,进一步通过讨论惯性系速度变换公式的单调递增特性,由变量有界的单调递增函数都有上限的特性, 进而利用相对性原理证明了普适极限速度的存在,由此可以完全确定惯性系的时空线性变换系数,从而推导出广义洛伦兹变换公式。在通常的文献和教科书中,往往都是通过引进光速不变假设来推导洛伦兹变换公式,这容易给人造成一种似乎无需用到相对性原理的假象,但是利用光速不变假设来推导洛伦兹变换需要事先假定时空变换为线性变换,即事先要求变换系数为常量,进而可以利用光速不变条件通过类光事件的特例来确定常量变换系数,因此时空线性变换是推导洛伦兹变换的前提。许多教科书和文献为了推导上的简明,对于惯性系的时空线性变换特性往往省略了证明或未给予严格的证明[10]。本文的讨论则说明了相对性原理是推导惯性系时空线性变换的必要条件,即使利用光速不变假设来推导洛伦兹变换公式，实际上也离不开相对性原理。这使得我们能够更好地理解相对性原理在相对论中的核心地位和所起的关键性作用。

感谢浙江省自然科学基金(编号：LY17A050001)对于我们相对论研究课题的鼓励和资助，同时也感谢与美国普林斯顿高等研究院Einstein Postdoctoral Fellow戴亮的有益讨论。

■