小钨球侵彻单兵防护装备的弹道极限

2018-08-31智小琦范兴华徐锦波

兵器装备工程学报 2018年12期

王帅，智小琦，范兴华，徐锦波

(1.中北大学机电工程学院，太原 030051； 2.晋西集团，太原 030027)

防弹衣、防弹头盔是单兵的生命屏障，对于维护单兵安全、增强环境适应性、提高战斗力都有重要现实价值。破片、枪弹等威胁会导致挤压伤、软组织伤、冲击伤等伤型，是防弹衣和防弹头盔防护的重点[1]。关于此方面的研究国内外有很多报告：邹渝等研究了单兵防弹衣对穿甲破片的防护效应，所用破片为美军标Mil-P- 46593A-2破片[2]；李常胜等研究了制式枪弹对软体防弹衣的侵彻规律，所用弹丸是51式标准铅芯弹，弹头质量5.5～6.3 g[3]；董萍等用数值仿真方法研究了手枪弹对带软体防弹衣人体躯干靶标钝击作用，所用弹丸是9 mm手枪弹，质量在5 g以上[4]；Freita 等研究了防弹头盔受到枪弹冲击时对人体的防护效果，所用弹丸为NATO标准9 mm手枪弹、7.62×39 mm中间威力弹和7.62×51 mm全威力弹[5]；Jolly等模拟了不同弹速撞击穿有不同型号复合防弹衣后的力学响应，所用弹丸为某型标准制式弹丸，质量为12.44 g[6]。上述对防弹衣、防弹头盔的侵彻均是以大尺寸破片或者标准制式枪弹为研究对象，而对小质量破片尤其是质量在0.5 g及以下的小钨球破片侵彻靶板的研究鲜有报道。

增加破片数量是提高单兵破片战斗部的毁伤能力的一个有效手段，在有效的空间内装填更多的小质量破片，提高毁伤威力。钨球破片密度大，强度高，存速能力强，更能使毁伤威力进一步提高。

本文用实验方法研究0.16g小钨球侵彻防弹衣和防弹头盔的弹道极限。在此基础上采用数值仿真方法研究防弹衣和防弹头盔与LY12CZ硬铝靶的等效厚度并探究不同小质量钨球侵彻防弹衣和防弹头盔时的侵彻规律，以期对单兵破片战斗部的设计提供指导作用。

1 实验

1.1 实验准备

靶板为防弹衣、防弹头盔和 2 mm厚的LY12CZ硬铝板。防弹衣的型号为2-583J，衣长590 mm，衣宽450 mm，由衣套和防弹层构成，衣套为涤纶，防弹层为III级凯夫拉；防弹头盔的型号为FDK2 F-CH02-L，正面宽度243 mm，侧面宽度275 mm，高度173 mm，由盔套和防弹层构成，盔套为涤纶，防弹层为IV级凯夫拉；凯夫拉是一种芳纶纤维材料产品，它具有密度低、强度高、韧性好、耐高温、易于加工和成型等特性，广泛应用于防弹衣、防弹头盔、坦克、装甲车、核动力航空母舰和导弹驱逐舰，使上述兵器的防护性能大为改观。

考虑到单兵武器体积小、质量轻的特点，为了增加单位体积内的破片数量，提高杀伤威力，拟选择质量为0.16 g、直径为2.8 mm的小钨球破片。发射装置为12.7 mm滑膛弹道枪，弹托材料为普通尼龙，直径12.7 mm，高度11 mm。发射时，破片随弹托飞出，弹托迎风面积大、阻力大，小钨球迎风面积小、阻力小，这样在飞出短距离内弹托和小钨球自动分离。

测速装置为NGL202-Z型测速仪，μs计时，利用断靶测试小钨球靶前速度或靶后速度，并记录侵彻状态。实验原理如图1所示，图2为钨球和弹托。

1.2 实验结果及分析

1.2.10.16 g小钨球侵彻防弹衣实验结果

破片为0.16 g小钨球，靶板为防弹衣，测试靶前速度和靶后速度，实验结果如表1所示，图3为实验后靶板状态图。

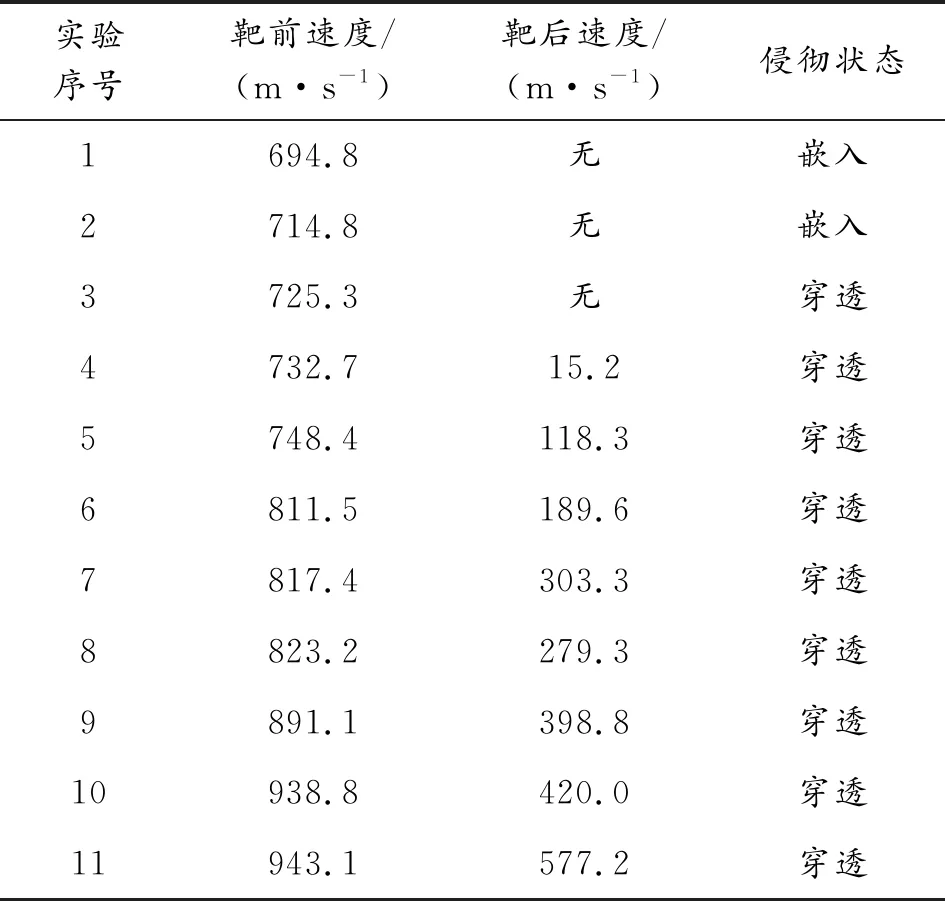
表1 实验数据

由表1可知：小钨球侵彻防弹衣弹道极限在725.3～732.7 m/s之间，由于两速度值较为接近，故取平均值[7]，则小钨球侵彻防弹衣弹道极限为729.0 m/s。

求弹道极限的经典方法Zukas模型[8]如下：

(1)

式中：LV0为靶前速度(m/s)；V1为靶后速(m/s)；V50为弹道极限(m/s)；α为常数。

由回归方法确定α≈0.985，V50≈729.4 m/s。

此时V1≈729.4 m/s，与上文采用平均值求得的弹道极限很接近，可以认为0.16 g钨球侵彻防弹衣的弹道极限约为729 m/s。

Zukas模型如下：

(2)

根据比动能计算式：

(3)

式中：e为比动能(J/cm2)；m为破片质量(kg)；V1为破片速度(m/s)；A为破片迎风面积(cm2)。

杀伤人体的最小比动能[9]e=160 J/cm2，由公式(3)可以计算得到0.16 g小钨球对人体造成杀伤的最小有效杀伤速度V1=253.7 m/s，将该速度作为0.16 g小钨球穿透防弹衣后的靶后速度，代入方程式(2)可得到小钨球此时的靶前速度V0=811.3 m/s，该速度即为 0.16 g小钨球穿透防弹衣后对人体具有杀伤作用的最小速度。

1.2.20.16 g小钨球侵彻防弹头盔实验结果

破片为0.16 g小钨球，靶板为防弹头盔，防弹头盔顶部厚度略小于四周[10-11]，所以在对侵彻防弹头盔的实验中，对防弹头盔顶部与四周分别做了侵彻研究。由于防弹头盔形状的限制无法测到靶后速度，只测得靶前速度，实验结果如表2所示，图4为实验后靶板状态图。

由表2可知：小钨球侵彻防弹头盔顶部弹道极限在741.0～751.4 m/s之间，由于两速度值较为接近，故取平均值，则小钨球侵彻防弹头盔顶部弹道极限746.2 m/s。同理可得小钨球侵彻防弹头盔四周的弹道极限为785.0 m/s。为确保一定的后效作用，选取侵彻防弹头盔四周的弹道极限作为小钨球侵彻防弹头盔的弹道极限。

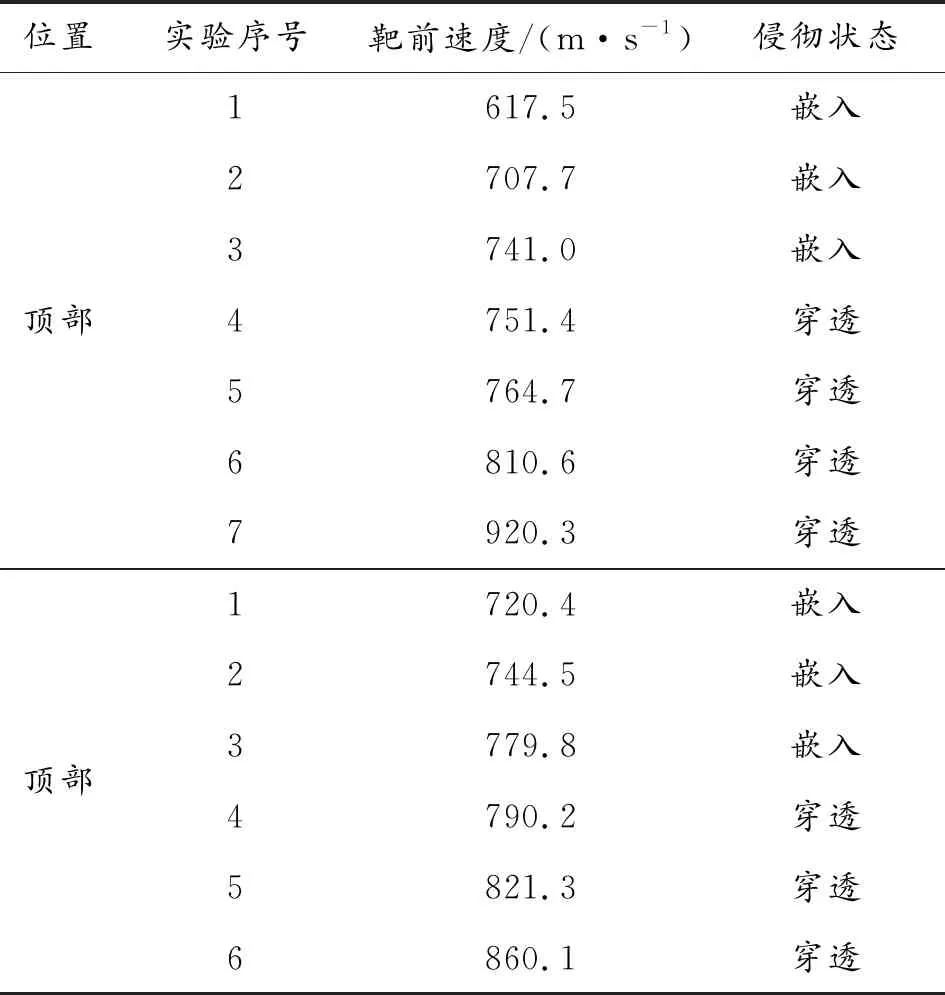
表2 实验结果

1.2.30.16g小钨球侵彻LY12CZ硬铝板实验结果

破片为0.16 g小钨球，靶板为2 mm厚LY12CZ硬铝板，并测试靶前速度和靶后速度，实验结果如表3所示，图5为实验后靶板状态图。

由表3可知：钨球侵彻LY12CZ硬铝板弹道极限在377.5～381.1 m/s之间，由于两速度值较为接近，故取平均值，则钨球侵彻LY12CZ硬铝板弹道极限为379.3 m/s。

如同式(1)，由回归方法确定α≈0.992，V50≈379.8 m/s，则Zukas模型如下：

(4)

此时V1≈379.8 m/s，与上文采用平均值求得的弹道极限很接近，可以认为0.16 g钨球侵彻2 mm厚LY12CZ硬铝板的弹道极限约为380 m/s。

数值仿真分析相对于传统的实验方法具有节约时间、成本、参数完善、结果可重复性高等优点[12]。为了探究不同质量的小钨球对防弹衣，防弹头盔的侵彻效果，采用数值仿真方法进行研究。

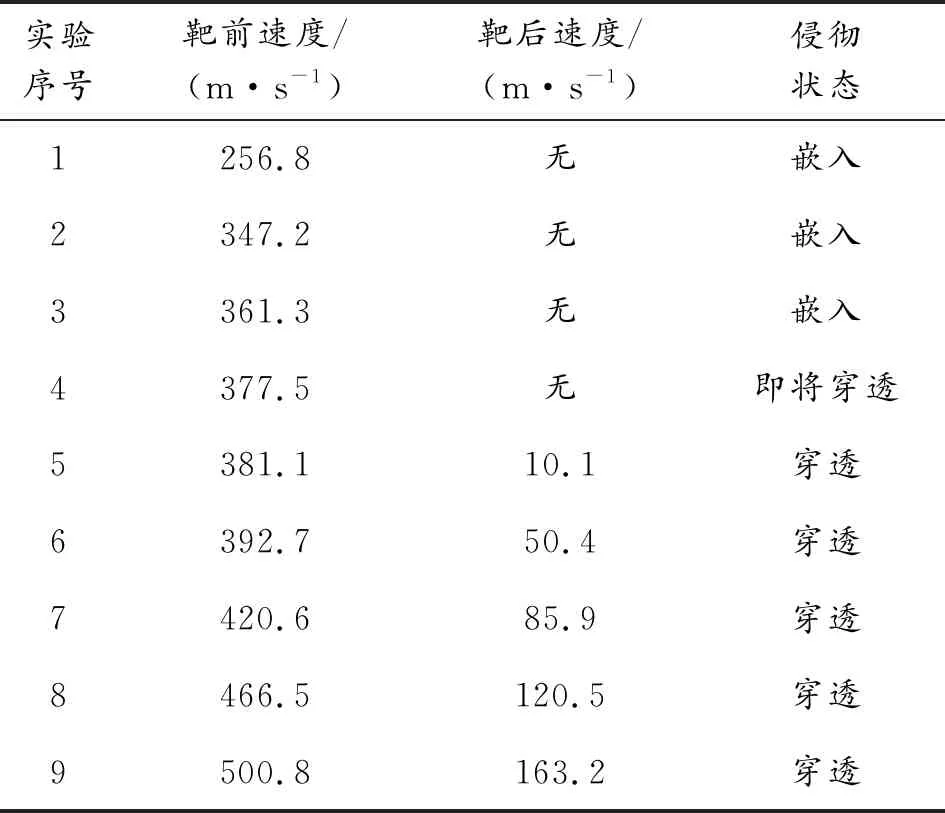
表3 实验结果

2 数值仿真

数值仿真采用有限元分析软件LS-DYNA，单位制为cm-g-μs，算法为Lagrange算法。在三维侵彻问题中，SOLID六面体实体单元是进行网格划分的首选，本研究对小钨球破片和LY12CZ硬铝板采用SOLID六面体实体单元，对网格进行局部加密，密集处网格尺寸为0.25 mm，稀疏处网格尺寸为0.5 mm。为了简化运算，根据结构的对称性，考虑到计算的时间和周期，建立四分之一有限元模型[13]，对称面采用对称边界条件，边界面采用非反射边界条件，如图6所示。

钨合金是一种具有明显应变率相关性的材料，故小钨球采用PLASTIC_KINEMATIC材料模型予以描述其力学行为[14]；LY12CZ硬铝靶靶板是高应变率材料，且侵彻过程中会产生冲击波，故采用JOHNSON_COOK材料模型和GRUNEISEN状态方程予以描述[15]。其参数分别如表4～6所示。

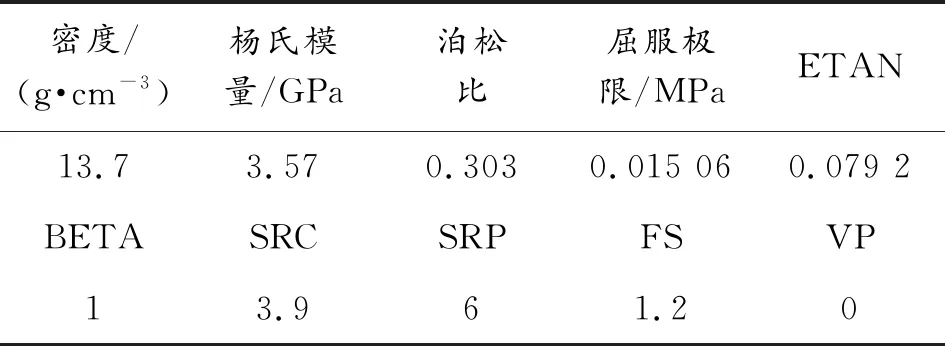
表4 钨球材料模型参数

(2) 钨合金密度和强度远大于LY12CZ硬铝板，应变率远小于LY12CZ硬铝板，故塑性下降对数值仿真结果的影响可以忽略。

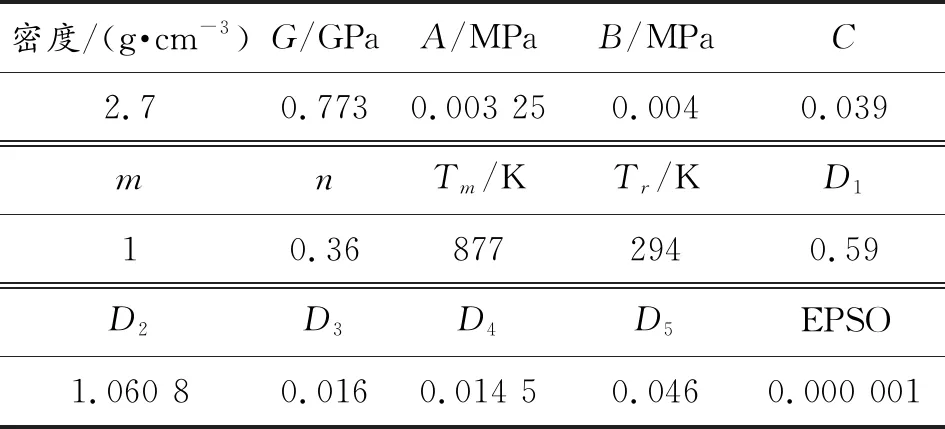
表5 LY12CZ硬铝靶材料模型参数

表6 LY12CZ硬铝靶状态方程参数

2.1 0.16 g钨球侵彻LY12CZ硬铝板数值仿真

表7为0.16 g小钨球侵彻2 mm厚LY12CZ硬铝板数值仿真结果。

由表7可知：钨球侵彻2 mm厚LY12CZ硬铝板时的弹道极限为380 m/s，可见数值仿真结果与实验结果比较吻合，材料参数可靠。

由于防弹衣、防弹头盔所用的凯夫拉材料结构比较复杂且数值仿真的物性参数难以获得，为了研究不同质量小钨球破片侵彻防弹衣、防弹头盔的弹道极限及其随质量的变化规律，本研究采用靶板等效方法，即LY12CZ硬铝板等效凯夫拉，虽然在材料特性上两者有所差异，但不同特性材料之间是可以进行等效的，如周岩等[17]把舰弦结构与DH36钢进行等效、杨玉林等[18]把陶瓷与装甲钢进行等效。LY12CZ硬铝板与凯夫拉的等效既能揭示侵彻规律又能简化计算的过程，研究结果对单兵作战武器战斗部的设计可以提供一定的指导作用。

表7 数值仿真结果

靶板的等效一般可以选用2种准则：一种是弹道极限方法；一种是剩余穿深方法，这里选用弹道极限方法。基于上述的有限元模型、材料模型和状态方程，分别用防弹衣的弹道极限729.0 m/s和防弹头盔四周的弹道极限785.0 m/s分别去侵彻不同厚度的LY12CZ硬铝靶，仿真结果如图8所示。表8为有关数据。

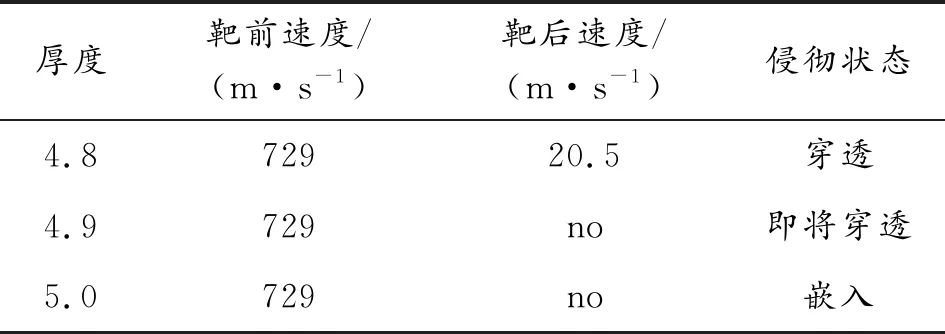
表8 防弹衣与LY12CZ硬铝靶等效厚度

由图8可以看出，靶板厚度4.8 mm时为穿透，4.9 mm时为即将穿透，5.0 mm时为嵌入，据此可以得出防弹衣的当量LY12CZ硬铝靶厚度为4.9 mm；同理通过数值仿真得出防弹头盔的当量LY12CZ硬铝靶厚度为5.4 mm。

为了分析弹靶相互作用中的尺度效应、破片的磨蚀和靶体的破坏响应等因素对等效厚度的影响，利用德·玛尔公式计算了0.16 g、0.2 g、0.25 g、…、0.5 g的小钨球侵彻防弹衣时的与LY12CZ硬铝板等效厚度，得到最大等效厚度与最小等效厚度之间的相对误差仅为1.96%。说明当小钨球破片质量在0.5 g以内时，弹靶相互作用中的尺度效应、破片的磨蚀和靶体的破坏响应等对等效靶厚度的影响很小，可以认为防弹衣与LY12CZ硬铝板的等效厚度为4.9 mm，防弹头盔与LY12CZ硬铝板的等效厚度为5.4 mm。

2.2 弹道极限及其随小钨球质量变化规律

为了研究小质量钨球侵彻防弹衣和防弹头盔的弹道极限随小钨球质量的变化规律，现以上述等效后的LY12CZ硬铝靶分别代替防弹衣和防弹头盔，模型网格划分方式同第2小节相似。用0.16 g、0.2 g、0.25 g、0.3 g、0.35 g、0.4 g、0.45 g和0.5 g的小质量钨球分别侵彻4.9 mm和5.4 mm LY12CZ硬铝靶，得到各自的弹道极限，再根据方程式(2)计算得到不同质量小钨球对穿有防弹衣人员有效杀伤速度，结果如表9所示。

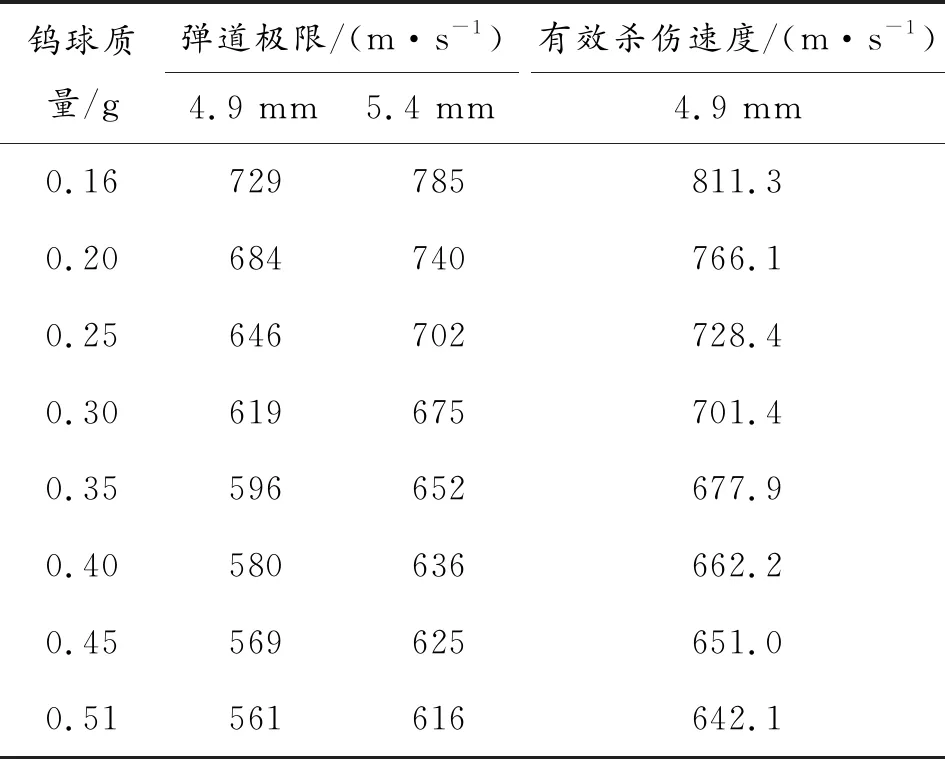
表9 不同质量钨球侵彻LY12CZ硬铝靶弹道极限和有效杀伤速度

由图9可以看出，小质量钨球侵彻防弹衣和防弹头盔时，弹道极限和有效杀伤速度随小钨球质量的变化规律基本一致，在0.16～0.35 g之间，两者下降速率很快，在0.35～0.5 g之间，两者下降速率明显减小，由于单兵作战武器要求战斗部体积小、质量轻，综合分析破片数量与弹道极限或有效杀伤速度的关系，采用0.35 g左右的小钨球破片既能保证有效毁伤速度不高，又能增加其单位体积内的破片数量，进而提高其毁伤威力。