管路阻尼敷层减振效果评估研究
2018-08-30尹志勇吴江海孙凌寒
尹志勇,吴江海,孙凌寒
(中国船舶科学研究中心 船舶振动噪声重点实验室,江苏 无锡 214082)
管路阻尼敷层减振效果评估研究
尹志勇,吴江海,孙凌寒
(中国船舶科学研究中心 船舶振动噪声重点实验室,江苏 无锡 214082)
摘要:文章对舰船管道外表面进行了不同面积粘性阻尼敷设,从理论、仿真和试验三方面对阻尼的损耗因子、管道的振动传递损失进行了分析,建立了包含阻尼减振措施的管路声学评估方法,获得了阻尼材料在管路振动控制方面的应用方法和和规律。研究结果表明:管道与阻尼层的截面惯性矩对阻尼吸振效果起着关键作用,由于截面惯性矩的作用,管壁上敷设约束阻尼要优于自由阻尼。同时阻尼敷设位置也影响着吸振效果。
关键词:约束阻尼;管路振动;振动控制
中图分类号:TB535+.1
文献标识码:A
doi:10.3969/j.issn.1007-7294.2018.08.014
文章编号:1007-7294(2018)08-1039-08
收稿日期:2018-06-27
基金项目:江苏省自然科学基金—青年基金(BK20160201)
作者简介:尹志勇(1981-),男,博士研究生,高级工程师,E-mail:wq_708@163.com; 吴江海(1989-),男,工程师。
Research on the isolation of pipe damping cladding
YIN Zhi-yong,WU Jiang-hai,SUN Ling-han
(National Key Laboratory on Ship Vibration&Noise,China Ship Scientific Research Center,Wuxi 214082,China)
Abstract:The loss factor and vibration transmission loss of pipes with damp cladding are studied.Vibration and acoustic evaluation method for pipes with damp cladding is developed and the application method and rules of damping material are acquired.The results show that the moment of inertia of pipe and damping have great influence on the vibration absorbing effect.For the pipe,constrain damping is better than the free damping.Also the damping location is of the same importantce.
Key words:constrained damping;pipe vibration;vibration control
0 引 言
管路在设备振动中扮演着传递者的角色,起着结构噪声传递的“声桥”作用,因此管路一直是减振降噪治理的重点对象。比较常用的治理管路振动的手段主要有两种:第一、在管路中串联挠性接管,隔离振动能量传递;第二、在管壁外敷设阻尼层结构,吸收并耗散振动能量[1]。阻尼处理常作为辅助技术措施应用于管路,但相关试验发现阻尼处理与挠性接管具有相当的减振效果[2]。
阻尼损耗系统能量从减振的角度来看,就是将机械振动的能量转变成热能、电能、磁能或其它形式能量而消耗掉,从而达到减振的目的[3]。阻尼技术就是充分运用阻尼耗能的一般规律,从材料、工艺、设计等方面发挥阻尼在减振方面的潜力,以改善机械结构的动态特性,降低机械产品的振动,增强机械或机械系统的动稳定性。管路阻尼减振一般是在管路表面贴上或涂上内损耗、内摩擦大的粘弹性高阻尼材料,使管路振动因阻尼作用而得到衰减,从而减少空气噪声的辐射。这样的结构形式说明,与流体直接接触的管壁材料、厚度没有改变,即阻尼减振不改变管路的原有结构,对系统的可靠性没有任何不利影响;其次,阻尼处理的范围从理论上讲可以不受限制,减振效果可以得到保证,适用于受弯曲振动为主的厚度不大的构件或薄壁零件。因此,该阻尼减振措施适合潜艇管路的减振降噪处理。管路阻尼处理技术在不改变管路承压强度和方便施工等方面具有自身的优势,具有十分广阔的应用前景。本文主要探讨管路阻尼敷层减振降噪效果仿真评估的方法。
1 管路阻尼覆层结构的理论分析方法
管路系统用的阻尼材料不仅要求材料本身阻尼性能优异,还要求有一定的柔韧性以便于管路的缠绕包覆。而一般常规的阻尼材料要么硬度比较高,要么阻尼性能较低,主要用于平面部位或曲率不大的部位。
粘弹性阻尼材料由于其阻尼性能优异、柔韧性好、易于包覆等特点,是管路中应用最为广泛的阻尼材料类型。粘弹性阻尼材料主要有沥青类阻尼材料和橡胶类阻尼材料[4-5]。橡胶类阻尼材料是利用橡胶本身所具有的粘弹性对结构进行阻尼减振,也是管路阻尼包覆中应用得最为广泛的一种材料。
目前常用的管路阻尼覆层减振结构有自由阻尼结构和约束阻尼结构[6]两种型式。直接将阻尼材料粘附在薄板上,称为“自由阻尼结构”;在构件表面上铺设阻尼层和约束层的结构称为“约束阻尼结构”,约束阻尼结构通过阻尼层在振动过程中承受交变变形来损耗能量,从而控制结构的振动。
自由阻尼结构和约束阻尼结构的理论分析方法主要有复刚度法、变形能法、模态分析法、有限元法等。其中复刚度法应用最为广泛,它通过利用材料力学和弹性力学的观点和分析方法,导出直接粘附阻尼结构的复刚度。在利用复刚度法进行表面阻尼处理结构分析时,假设:
①阻尼层与弹性层在弯曲振动时具有相同的曲率,忽略相对伸长;
②各层具有相同的振动模态,忽略振动过程中各层的厚度变化。
考虑到表面阻尼处理主要适用于受弯曲振动的结构,其复刚度表达式为:

式中:(EI)*为复弯曲刚度,(EI)′、(EI)″分别为其实部和虚部,η 为直接粘附阻尼结构的损耗因子。 损耗因子的大小就是迟滞阻尼的大小,它反映了结构振动时能量损耗能力的大小。
1.1 自由阻尼结构
图1为管道敷设结构示意图。带覆层圆柱管单元在弯曲时,使首端固支,在末端加一弯矩M,它与端面的转角关系为

式中:φ既是覆层又是管壁末端面的转角,两者都处于弹性状态,所以有:


式中:下标p为管路本身力学属性,下标c为阻尼层的力学性能。由材料力学的线弹性关系,有下式成立:

所以,EI=EpIp+EcIc
同理,损耗系数为:

图1 管道敷设阻尼结构示意图Fig.1 Pipe covered with damping

式中:
对于图2(a)所示具有自由阻尼敷层的矩形截面梁,基本层厚度H1,阻尼层厚度H2,梁为单位宽,x轴为中性层,弹性层和阻尼层的交界面离x轴的距离为δ,ω为挠度,y表示与中性层的距离。由复刚度法推导得到结构损耗因子为

式中:β为阻尼材料的损耗因子,为模量比;为厚度比。对比(7),(8)式可见具有自由阻尼层的圆截面管道与矩形截面梁的损耗因子表达式相差比较大,前者仅与管道和阻尼材料的弯曲刚度及各自的阻尼有关,而后者与二者的模量比和梁的高度比有关。主要原因在于管道阻尼层是对称布置而矩形截面梁是非对称布置。

图2 矩形截面梁自由阻尼与约束阻尼结构示意图Fig.2 Free damping and constrained damping of rectangular cross beam
1.2 约束阻尼结构
我们认为管道与阻尼层及约束层具有完全相同的横向位移,同时其弯曲模态也完全一致。这种假定是用复刚度法分析具有约束阻尼层的管道的弯曲刚度和损耗因子的前提。对于图2(a)所示具有一层阻尼材料和一层约束层的三层结构的管道其横截面上的弯矩是三层材料所受弯矩之和。

式中:EI为截面的复合弯曲刚度;Mi为第i层的弯矩;θ为截面的转角。

图3 约束阻尼层变形与受力Fig.3 Deformation and stress of constrained damping layer
为了得到EI必须先求出每层的弯矩。选取任意截面其相对于平衡位置的角位移如图3(b)所示,管道与约束层的转角为θ,阻尼层的剪应变为γ,忽略管道与约束层的剪切变形。这样管道与约束层的弯矩分别为:

式中:E1,E3为管壁与约束层材料的杨氏模量;I1,I3为管壁与约束层的截面惯性矩,
阻尼层由于既存在拉伸变形又存在剪切变形,其弯矩需要根据其具体的变形状态来计算。在管截面内建立图3(a)所示极坐标。在阻尼层截面上任意一点(α,r)沿轴向x的变形量 δ=rsin(α ) θ-(r- r0-h0)γ,该点的轴向应力,据此可以计算阻尼层的弯矩

式中:E2为阻尼材料的杨氏模量。
由于阻尼层各点的剪应力不是一个常量,要计算上式还必须通过对阻尼层进行受力分析获得剪切应变γ的表达式。管道截面各层材料的受力状态是比较复杂的,为将问题简化,假定在任意径向剖面上阻尼层与约束层的剪切应力可以忽略不计。这样在任意径向剖面上阻尼层与约束层交界面上的剪切力与约束层的轴向拉应力平衡(图3(c)),即有

根据上式可得到

式中:G2为阻尼材料的剪切模量。
将(13)式代入(11)式可计算得到:

如果管道做简谐振动则阻尼层的应变也做简谐运动,此时将有 γ=γ0sinαcos( kx),θ=θ0cos( kx)。 由此,可以得到:

由(13),(15)式以及γ与θ的简谐变形规律得到

式中:g为剪切参数,
将(10)、(14)和(16)式代入(9)式可求得管截面的复合弯曲刚度:

令 EI=E′I( 1+jη ),EiIi=Ei′Ii(1+ jηi),其中 η 是截面总的损耗因子,ηi是第i层的损耗因子(i=1,2,3)。如果忽略管壁和约束层的损耗因子,根据上式计算得到截面总损耗因子表达式如下:

式中:
图5~7是DN80管道上包覆一层厚h1的阻尼材料和一层厚h2的约束材料,其损耗因子与频率和阻尼材料厚度之间的关系。管道材料与约束层都是钢质。阻尼材料是橡胶,其杨氏模量和损耗因子如图4所示。

图4 阻尼材料杨氏模量与损耗因子Fig.4 Yong’s modulus and loss factor of damping material
2 带有约束阻尼层的圆截面管道减振效果研究
2.1 覆层材料复杨氏模量测量
由橡胶材料的性能影响因素可知,橡胶材料的特性参数随频率和温度会发生变化,无法精确获得,因此很难通过解析或数值手段得到其动力特性参数。本文应用了一种通过小型橡胶试件的动刚度 (位移阻抗)的测得值和试件的尺寸系数推算出其纵向或剪切变形的复弹性模量及其损耗系数的测试方法。并根据测试要求加工出圆柱体试件的小样,使用一套粘弹性材料动态特性测量装置对圆柱体橡胶试件进行了测量,测出了在室温为15℃时5 Hz~1 kHz频率范围内圆柱体试件材料的复杨氏模量和损耗系数。
2.1.1 测试原理
对于一个圆柱体结构的压缩变形,其复杨氏模量和拉压动刚度存在如下的关系:

图5 损耗因子与频率及阻尼层厚度的关系Fig.5 Relationship among loss factor and thickness of damping and frequency

图6 损耗因子与频率及约束层厚度关系Fig.6 Relationship among loss factor and thickness of constrained and frequency


图7 损耗因子与频率及阻尼材料杨氏模量关系Fig.7 Relationship among loss factor and Yong’s modulus of damping material and frequency
式中:S为试件的横截面面积;h为试件的高度。
由上式可以得出复杨氏模量及其损耗系数:


式中:imag(*)为*的虚部;real(*)为*的实部。
由以上可知,只要测得试件的拉压动刚度就可以计算出其复杨氏模量和损耗系数。
2.1.2 测试结果
图8所示为橡胶复杨氏模量(左)与损耗系数(右)测量结果。从图中可以看出,在5 Hz~1 kHz的频率范围内,橡胶的杨氏模量幅值和损耗系数都呈现单调增加的趋势。如果将5 Hz的测量结果当做其静态特性,则在1 kHz其杨氏模量幅值变为原来的1.65倍,损耗因子增加为原来的4倍。由此可见橡胶阻尼材料复模量的这种随频率变化的特性将对其阻尼效果产生重要影响。
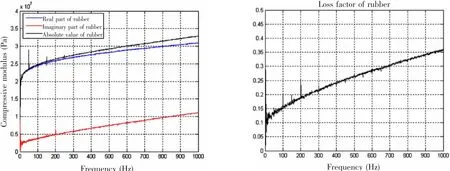
图8 管道阻尼包覆材料复杨氏模量与损耗系数测量结果Fig.8 Test result of Yong’s modulus and loss factor of damping material
2.2 敷设约束阻尼层的圆柱管单元的振动传递试验
由于具有自由阻尼层的管道损耗因子仅与阻尼材料和管道的弯曲刚度之比有关,要获得较好的阻尼特性,要求阻尼材料具有较大的杨氏模量。一般橡胶类阻尼材料的杨氏模量量级在107~108之间,与钢材相差3~4个数量级,因此阻尼效果微乎其微。相比之下,约束阻尼结构由于阻尼材料的剪切运动,阻尼效果比较明显。为了对约束阻尼结构的损耗因子计算公式(18)式进行验证,对一段包覆约束阻尼的管道进行了振动传递试验。管道及阻尼材料参数如下:
管道:长1.8 m,内径80 mm,壁厚4.5 mm,Q235钢无缝钢管;
阻尼层:7 mm厚丁基橡胶板;
约束层:0.8 mm厚镀锌板。
该阻尼结构的包覆工艺是先将阻尼层与约束层硫化成一张500 mm×500 mm的板然后根据管道外径将板裁剪成长500 mm,宽约160 mm的矩形板,在模具内弯曲成型,最后用环氧树脂胶粘贴定位、固化。管道用2根橡皮绳水平悬吊,一端安装力传感器、加速度计,另一端安装加速度计,将力传感器与激振机激振杆连接,用白噪声对管道进行激励。根据管道两端加速度可以获得阻尼对管道振动的衰减作用。
图9为约束阻尼管道激振试验示意图。本试验共进行了如下3个工况:
工况1:阻尼敷设长度为1.5 m;
工况2:阻尼敷设长度为1.0 m;
工况3:阻尼敷设长度为0.5 m。
图10是这三个工况的阻尼敷设的示意图。在工况1和工况3,阻尼在纵向是对称布置,在工况2,阻尼敷设位置与工况1一致,但减掉了靠近激励点的0.5 m长的阻尼。

图9 约束阻尼管道激振试验Fig.9 Excitation test on constrained damping pipe

图10 三个工况下的阻尼敷设示意图Fig.10 Three operation conditions of damping laying
图11是三个工况下管道振动传递损失与未敷设阻尼的管道传递损失对比曲线。从图上观察,阻尼主要在管道共振频率附近起减振效果,而且大体上在高频的阻尼效果优于低频,低频的阻尼效果几乎可以忽略。虽然图5~7表明约束阻尼层的损耗因子随频率单调增加,但实际表现出来的对振动的衰减效果却并不一定如此。这说明实际的阻尼效果还取决于结构的振幅,振幅越大则减振效果越明显。对比三种阻尼敷设方式,虽然阻尼层沿纵向的长度变化较大,但对振动的衰减作用总体上变化并不大,在部分频段,后两种工况的阻尼效果甚至较第一种要好。这充分说明在对管道敷设阻尼时,并不一定要覆盖整个管段,应该根据管道上的振动分布来确定阻尼的敷设位置和长度。
图12、13是对一段具体的舰船通海管路进行动力学特性计算,以用来分析阻尼层的厚度与杨氏模量的影响。阻尼对管路振动的衰减作用随阻尼材料的厚度、模量的变换比较明显,但是要获得满意的减振效果,阻尼材料的厚度和杨氏模量要相当大,实际情况下难以实现,所以应该通过合理地设置阻尼材料在管道上的布置位置及沿管轴向的长度来提高减振效果。
3 结 论

图11 三个工况下管道的振动传递损失曲线Fig.11 The vibration loss factor of three operation conditions

图12 管道振动级随阻尼层厚度变化Fig.12 Relationship between vibration acceleration and thickness of damping layer
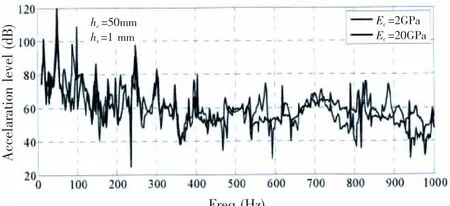
图13 管道振动级随阻尼材料杨氏模量变化Fig.13 Relationship between vibration acceleration and Yong’s modulus of damping layer
本文对敷设阻尼材料的管道的损耗因子和振动传递损失进行了理论和数值仿真分析,主要目的在于进一步完善包含阻尼减振措施的管路声学评估方法,同时探究阻尼材料在管路振动控制方面的应用方法和规律。通过实验和仿真分析,本文获得了如下结论:
(1)自由阻尼层对管道的阻尼作用主要同阻尼层与管道的截面惯性矩之比有关,由于管道截面惯性矩通常比板的大,自由阻尼在管道上的阻尼效果比板上效果小。而且一般的橡胶阻尼材料由于模量低于管材3~4个数量级,阻尼效果很微弱;
(2)约束阻尼层对管道的阻尼作用不仅与阻尼材料杨氏模量有关还与约束层和阻尼层的截面惯性矩比有关。在约束层不产生翘曲变形的条件下,其厚度越小则越有利于提高阻尼材料的阻尼效果;
(3)管道阻尼的减振效果同阻尼材料在管道上的敷设位置关系较大,振幅越大阻尼效果越明显。
