极点提取算法研究现状

邢煦然，贾 鑫，赵宏钟

(航天工程大学 a.研究生院； b.电子与光学工程系， 北京 101416)

根据目标特性理论可知,当雷达信号的波长与目标的特征尺寸相当的时候，目标处于谐振区，雷达回波中会存在谐振现象。与常见的光学区雷达目标散射回波不同，雷达目标在谐振区的最主要特性就是可用极点描述。极点对目标相对姿态、雷达极化方式等不敏感，只与目标本身的大小、形状、材料等因素有关，不同的目标具备不同的极点集[1-5]。因此极点可以克服轨道编目对变轨目标失效的缺陷和光学区雷达成像存在的姿态敏感性[6]，是一种稳健的目标识别途径，具有巨大的应用前景。从雷达回波中提取出目标的极点是使用极点特性进行目标识别的前提。

1 奇点展开理论

20世纪60年代，数值电磁学的发展，尤其是矩量法的提出，使得一些简单几何目标的瞬态散射得以计算。由于当时的计算目标主要是细导线这一类简单的目标，其散射表现出强烈的谐振特性，使得人们开始研究目标的谐振问题。1971年，Baum在研究雷达回波时，将雷达回波的后时部分用复衰减指数和来逼近，在复频域上可以用极点和留数表示[7]。此后，经过Marin和Ramm等[8-9]的研究和论证，完善了奇点展开法(the Singularity Expansion Method，SEM)的数学基础。SEM作为一种瞬态电磁响应求解的方法被提出，发展成为谐振区电磁特性的指导理论，其推导过程本文不做过多讨论，只给出其在谐振区雷达信号性质上的重要结论。SEM理论的主要内容为：雷达目标的传递函数可以表示为一个有理函数和一个整函数之和。

(1)

其中，ri为留数，si为极点，si=σi+ωij，其中σi为衰减因子，ωi为角频率，M为极点个数。其中整函数部分C(s)对应于系统时域上的前时响应，也是受迫响应，这一部分描述雷达目标的散射中心特性。有理函数部分对应于系统的后时响应，也是自然响应，这一部分描述雷达目标的极点特性，其时域对应复衰减指数和信号。

(2)

简单导体目标的谐振现象可以用爬行波现象解释，几何体的特征长度P与电磁波的频率f的关系是

(3)

其中m≥1且为整数。也就是说，波长的整数倍等于特征长度时，发生谐振，在此频率范围产生极点。当m=1时，谐振频率f1是目标的基带谐振频率；m>1时，fm称为谐波频率[10]。

下面列举球体的特征长度与极点，以说明它们之间的关系。假设半径为0.5 m的导体球，其极点理论值为[11]

-3.0×108+5.196 0×108i

(4)

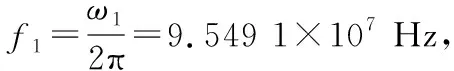
2 极点提取的时域算法研究现状

SEM揭示了极点对姿态不敏感的优良特性，使之成为雷达目标识别研究的热点。至今为止大部分研究致力于在后时响应信号中提取极点。

1975年，Blaricum等[12]首次将Prony方法应用于时域回波信号的极点估计中，这是最早的极点提取算法。Prony法通过求解多项式的零点获得极点，其缺点在于没有区分前时响应和后时响应，方程病态问题没有解决，而且对噪声敏感。诸多缺陷导致Prony法不能被广泛应用。之后的学者对Prony法做出了多种改进以提高其性能。其中比较经典的是1982年Kumaresan等[13]提出的SVD-Prony法，也叫KT法，KT法在Prony法的基础上增加了线性矩阵的维数，采用后向线性预测矩阵，并对预测矩阵做奇异值分解(SVD)，其抗噪能力较原始的Prony法有所提升。在KT法的基础上，1987年，Rahman等[14]将整体最小二乘技术运用于求解方程的过程中。1997年，Li等[15]使用低秩迭代逼近的方法处理预测矩阵，得到了更低的噪声门限。此后，Lee[16-17]对Prony法的信号采样做了改进。匡纲要等[18]提出了基于高阶矩的改进Prony法，将高阶矩的统计特性与Prony法高分辨性能有机地结合起来，其过程包括构造一个扩阶三阶矩矩阵、奇异值分解、确定阶数和求解方程，该算法的有效信噪比达到-10 dB。然而这些改进都没能克服Prony法本身的病态问题。

为了克服Prony法的固有缺陷，研究方向转为提升算法本身的精度和抗噪能力。1981年，Jain等[19]提出了函数束法。与Prony法相比，函数束法有更强的抗噪能力，其缺陷在于求解过程中存在参数估计，会导致误差积累，而且计算精度受滤波器选择影响。1989年，Hua等[20]在函数束的基础上，提出了广义函数束法，解决了函数束法的误差积累问题，该方法又称为矩阵束法(Matrix Pencil Method，MPM)。矩阵束法摒弃了多项式方法先求解方程组再计算高次多项式零点的思路，首先用信号构造Hankel矩阵，然后对Hankel矩阵奇异值分解，最后构造矩阵束求解广义特征值获得极点。矩阵束法抗噪性强，运算效率高，成为一种广泛应用的极点提取算法。此后Sarkar[21-22]又研究了矩阵束法的束参数和目标极点个数的估计方法，并通过实验分析完善了矩阵束法。2002年，Sarkar[23]通过对同一目标的多角度数据同时处理获得了目标的极点，这一方法克服了单一角度下矩阵束法因某些留数过小造成的极点丢失。2008年哈尔滨工业大学伍光新[24]提出了改进的总体最小二乘矩阵束法。该方法是通过遍历可能的阶数分别使用矩阵束法求解极点，而后由得到的极点分别重构信号。重构信号与原信号比较均方误差，误差最小者对应的个数即为极点个数。该方法是一种极点个数估计的可靠准则，但估计阶数往往大于真实极点个数。2012年哈尔滨工业大学邓文斌[25]提出了另一种确定极点数目的算法。他在研究过程中发现不同阶数时计算出的极点中，真实极点呈现出聚集特性，而虚假极点则随机分布。利用这一现象，他通过提取不同极点个数时的极点，观察它们的聚集程度确定极点个数。该方法原理简单，但是存在参数人为选取的问题，限制了其应用。矩阵束法综合性能强，但也存在问题。首先，矩阵束法对束参数和模型阶数敏感[26]，在使用时获得参数的过程往往比算法本身更复杂，而得到的参数往往不是最优；其次，矩阵束法是整体估计算法，一个极点的错误估计可能影响到其他极点。

极点估计的非线性模型算法中，最具代表性的是E脉冲法和迭代法。E脉冲是指一种特殊的雷达入射波型，当它激励特定目标时，使目标的后时响应为零[27-28]，这一特性使E脉冲成为一种有效的雷达目标识别方法。使用E脉冲识别目标，首先获得目标极点，然后根据极点合成E脉冲，最后用E脉冲激励目标，如果回波的后时响应为零那么就确定了目标。在此基础上，1987年Rothwell[29]提出，在已知目标冲击响应的条件下，可以利用E脉冲技术反求目标极点。E脉冲法等价于对冲激响应进行卷积和平滑后再使用广义Prony法求取极点，因此其噪声特性优于广义Prony法[30]，但是该方法计算量大，结果受时间参数影响，因此实用性价比不高[26]。迭代法是1985年由Drachman[31]首次提出，迭代法的思路是将极点提取问题转化为优化问题，每次通过优化算法估计目标的一对极点，直到估计出目标的所有极点。通过对优化算法的改进已经发展出很多种，已应用的优化算法包括：进化算法[32-33]、下降算法(Gauss-Newton算法、Levenberg-Marquardt算法)[33]、遗传算法[34]、有理逼近[35-36]等。迭代类算法的优势在于总是优先提取出留数大的极点，在提取之前不需要估计极点的个数，因此估计精度不受极点数目的影响。迭代法的共性特征在于：需要迭代初值；误差累积；极点多时运算量大[35]。

极点估计的时域算法依赖于后时响应信号的准确性，由于实际中不能实现冲激响应激励目标，所以得到的信号同时存在前时响应和后时相应。根据信号与系统理论，系统前时响应中受迫响应为主但是自然响应也同时存在；实际上，因为目标在入射波方向有长度，后时开始时仍有前时响应信号传播导致混叠。因此，极点提取的时域算法都会存在早晚期响应混叠缺陷。归纳已有的几大类算法，其缺陷如表1所示。

表1 极点提取时域算法的缺陷

3 极点提取的频域算法研究现状

极点提取的频域算法直接从频率响应数据中获得目标的极点，是极点提取的另一种思路。频域方法通过采集的频率响应数据，参数化目标的谐振区传递函数，然后求解传递函数的极点。最早出现的频域方法是1977年Moffatt等[37]在研究金属导线的谐振效应时，通过有理近似的方法从频域数据中获得了电路系统的极点。这一算法虽然不是雷达目标的极点问题，但数学模型十分相似，为后来的雷达目标极点估计提供了思路[10]。1990年，Kumaresan[36]针对由频域响应数据参数化传递函数的问题提出了频域Prony法，这一方法后来被用于极点提取问题中。以上两种方法都没有克服极点估计的病态问题，因此限制了其应用。1994年，Bertocco[38]提出了一种基于频域插值的衰减正弦信号分析方法，并对仿真数据进行了算法验证。1996年，焦丹等[35]提出了基于有理逼近的极点提取方法，首先通过样条拟合去噪，然后在频域上有理逼近获得极点。1999年，焦丹[39]又提出了先使用频域紧支集正交小波基对信号去噪，然后再最优一致逼近的方法。2004年，Wang等[40]提出了用ARMA模型参数化传递函数，然后用最小二乘法估计极点的方法，并对细导线进行了验证。2007年，Chauveau等[10]使用有理近似法和频域Prony法对仿真目标进行了窄带频域数据极点提取的仿真实验，这是已有的唯一一种窄带条件下的极点提取算法。2008年，伍光新[36]提出了另一种有理逼近的方法，通过正交矢量拟合迭代的方法参数化传递函数，算法考虑到病态问题，在简单目标和复杂目标的仿真实验中都获得了准确的结果，但算法的逼近精度和极点准确度之间存在矛盾。

极点提取的频域算法研究相对时域算法较少，其原因在于不能避免前时响应在频域的影响，也无法在算法模型上避开病态问题。但是极点估计的频域算法可以避免时域算法中的截断问题、前后时区分问题，更重要的是具有从窄带数据中提取极点的能力，是一种非常有前景的极点提取方向。

4 结论

1) 极点在的优良特性使其在目标识别方面有很大的应用前景，但是由于苛刻的信噪比和带宽条件，当前仅被应用于无源标签[41]和暗室实验中，继续研究和改进极点提取方法，具有重大的工程和学术价值。

2) 当前，对于极点提取算法的研究主要集中于简单几何目标，提取结果与电磁学计算结果相比较，验证算法性能。但是对于复杂目标，首先不能直接计算其极点理论值，无法验证算法提取结果是否准确；其次复杂目标的谐振现象复杂，提取中往往出现大量虚假极点，影响其作为目标识别标准的适用性。研究复杂目标的极点提取算法是将极点应用于工程中的前提。

3) 极点提取算法基于超宽带数据，然而大部分现役雷达不具备超宽带能力，为了提高极点的工程价值，研究基于窄带数据的极点提取算法具有重大的工程价值。

4) 当前极点提取算法适用的信噪比极限在-10dB左右，依然远高于雷达设备的信噪比。继续提升极点提取算法的抗噪能力，是将极点识别应用于工程中的另外一个重要条件。