采用傅里叶拟合的双天线信号端点识别方法

屈文星，李炎倍，李云祥，李建玉

(中国人民解放军63788部队， 陕西 渭南 714000)

弹道导弹目标在飞行过程中为保持较为良好的定向性与姿态稳定性，常采用自旋的方式，即在弹体质心平动的同时，引入围绕弹轴的自旋运动[1]。此类自旋运动会对某型双天线应答式目标的下行信号产生频率调制，在多普勒频率中引入边带分量，称之为微多普勒频率[2]。由于双天线目标的弹体遮挡效应，会使下行信号中的微多普勒频率产生与天线轮序切换节点相互对应的阶跃，使其时频特征表现为半周期斜升正弦曲线[3]，导致在微多普勒项的信号模型表述中产生较为复杂的描述参数项，对于信号处理算法的应用与信号数据分析不利。

为了实现更为完备而简捷微多普勒频率表述，完成对微多普勒频率阶跃的消除，工程中可通过对双天线信号的双路分离，对单天线支路信号进行处理。由于微多普勒频率的阶跃处与双天线信号端点相互对应，可通过对双天线信号的切换端点进行识别，基于此,本文提出了一种采用傅里叶拟合的双天线信号端点识别方法，首先通过对双天线信号的一阶差分处理，为获取精确的信号端点，需要克服噪声带来的数据不平滑影响[4]，本文采用傅里叶曲线拟合对端点信息进行平滑处理，并通过极值搜索获取精确的信号端点时间信息，即可在信号存储区完成双路信号的分离。

1 双天线信号

1.1 微多普勒时频特征

信号时频特征反映了信号频率随时间变化的规律，根据应答式旋转目标的微多普勒模型[5]可知，自旋引起的微多普勒调制信号其时频特征表现为周期性的正弦曲线。如图1所示。

对于两幅轮序工作天线(P1与P2)的导弹目标，由于目标的弹体遮挡效应[6]，单天线P1在图1中有效的雷达覆盖范围为D-A-B段，相反B-C-D此段内的信息处于缺失状态。在其他条件不变的前提下，对称放置的天线P2与天线P1仅在时频域上有大小为π的相位差，微多普勒频率变化特征相同。

因此双天线的微多普勒特征表现为周期重复的半周期斜升正弦曲线，即在天线切换处会出现频率阶跃。理论接收信号中的微多普勒时频特征如图2所示[3]。

1.2 基频信号模型

根据文献[3]可知，接收信号调制特性应考虑平动多普勒、微多普勒以及天线方向性的共同调制作用，基频信号模型可表示为：

s(t)=a(t)Ptexp(j(2πfbt+2πfd(t)+φ(t)))+n(t)=

exp(j(mfsin(2πfmt+φm)))+n(t)=

a(t)Ptsc(t)sT(t)sm(t)+n(t)

(1)

式(1)中，a(t)为天线幅度调制函数；Pt为空间链路损耗；sc(t)为基频载波分量；sT(t)为平动多普勒分量；sm(t)为微多普勒分量；n(t)为高斯白噪声。

基频信号的时域波形与微多普勒特征如图3所示。

2 信号端点识别

2.1 差分变量法

对于信号频率阶跃处的端点提取可采用变量差分法[7]，以获取双天线的切换时刻。具体算法表述如下：

设T时间内的采样数据点在采样间隔ts下为x1,x2,x3，…,xT/ts，对其进行一阶差分，其结果Δxi可表示为：

Δxi=|xi+1-xi|，i=1,2,3，…，T/ts

(2)

根据前文分析可知，因旋转双天线产生的频率阶跃与目标自旋频率和天线方向性有关，其频率阶跃范围与时频特征周期均为定量值。以单天线周期长度Nm为滑动窗口，取Nm位数据中Δxi的极值，即可获得双天线信号的时间端点。其中Nm可表示为：

Nm=⎣2Tfmfs」

(3)

式(3)中，fs为采样率，⎣·」为向下取整。通过门限提取可得Nm位结果中的极小值Δxmin i，i=1,2,…，Nm。寄存极大值Δxmini的时间位置信息记为t(Pl)，Pl代表天线选择，每一段位置信息(两组为一段)分别为：tbegin(Pl)与tend(Pl)，理论信号端点的起始位置如图4所示。

理想条件下，通过提取一阶差分结果的谷值，即可得双天线切换时间端点。受信号信噪比环境与时标偏移等因素的影响，一阶差分处理结果无法获得较为准确的谷值。因此需对处理结果进行曲线拟合，在本文中采用了傅里叶曲线拟合的方法。

2.2 傅里叶曲线拟合

曲线拟合是利用平滑曲线拟合多个离散数据[8]，是数据分析与数据平滑较为常用的方法之一，拟合曲线会尽可能接近离散数据点，但并非全部通过。傅里叶拟合通过傅里叶级数的不断逼近，实现离散数据的平滑处理，是一种较为常用的曲线拟合方法[9]。

结合双天线信号的周期性，可采用基于周期函数傅里叶级数展开原理的傅里叶拟合方法，可取得较为平滑的差分结果，利于时间端点谷值的提取。其拟合函数表示为：

i=1,2,…,n

(4)

式(4)中:a0与w为常系数；ai与bi为各级系数；n为傅里叶展开级数；Yfit(t)为拟合所得曲线。对微多普勒信号做一阶差分处理，并对其结果傅里叶拟合。由式(4)可看出，当傅里叶展开级数n越高，所得拟合结果应更为平滑，相应的计算次数也会随之增加，因此在傅里叶拟合过程中，傅里叶展开级数的选择需要权衡平滑效果与计算效率。

通过对拟合曲线的谷值提取，可得信号在天线切换处的时间端点t(Pl)，通过时间轴端点区分可得单天线信号时间位置tbegin(Pl)与tend(Pl)，即可获得双天线对应的支路信号。

3 仿真与分析

设置仿真自旋频率为0.5 Hz/s，旋转半径为1 m，模拟方位角为125°，空间俯仰角为10°，多普勒频率无变化率，应答机工作于C频段，取5 GHz，其转发系数为0.9，观测时长7 s，其中单天线信号的周期为1 s。分别通过仿真信号与实测信号对上述方法进行检验。

3.1 理论信号验证

通过分别设置两类噪声环境：一类为无噪声理论信号，另一类为加噪仿真信号，其信噪比为30 dB。根据上述信号模型与端点识别方法，可得不同环境噪声下的仿真信号时域波形。如图5所示。

对所得两类信号进行一阶向前差分处理，所得结果如图6所示。

对加噪信号的一阶差分处理进行谷值提取，可得单天线(P2)信号时间端点提取结果如表1所示。

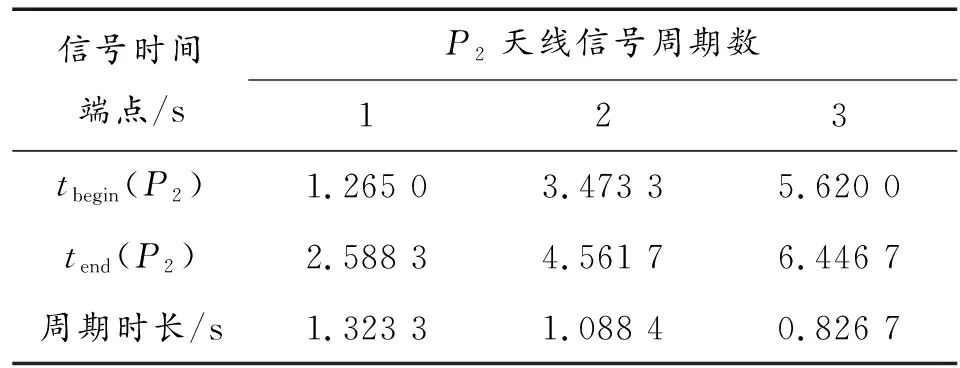
表1 单天线信号的时间端点提取结果

可以看出在信噪比为30 dB的情况下，所得提取结果单天线周期时长与实际值(1 s)误差，即加噪信号的一阶差分处理结果无法获取精确的谷值，进而验证了通过傅里叶拟合完成数据平滑的必要性。

3.2 实测信号验证

本文仿真试验中所用实测信号为某型旋转导弹微多普勒试验模拟平台所产生的模拟双天线下行信号。旋转目标微多普勒试验模拟平台由微动目标模拟台、信号发射端与信号接收端组成。目标模拟台可模拟目标在空间的飞行姿态，安装于模拟台上的应答机模拟双天线下行信号，应答机天线随转台做连续转动。试验平台样机工作原理如图7所示。

取与上述参数设置一致的实测信号，自旋频率为0.417 Hz/s(150°/s)，单天线周期为1.199 s，信号总观测时长为143 s，截取信号时长为7 s，记录所得实测信号时域波形如图8所示。

对截取段实测信号进行一阶差分处理，并设曲线拟合中傅里叶级数为6，对一阶差分结果进行傅里叶拟合，完成信号端点的识别处理，其结果如图9所示。

其中傅里叶拟合函数的常系数与各级系数如表2所示。

表2 差分结果拟合所得傅里叶拟合函数的各级系数

通过提取傅里叶拟合曲线的谷值，可得双天线实测信号端点，取P2天线信号的时间端点，其提取结果如表3所示。

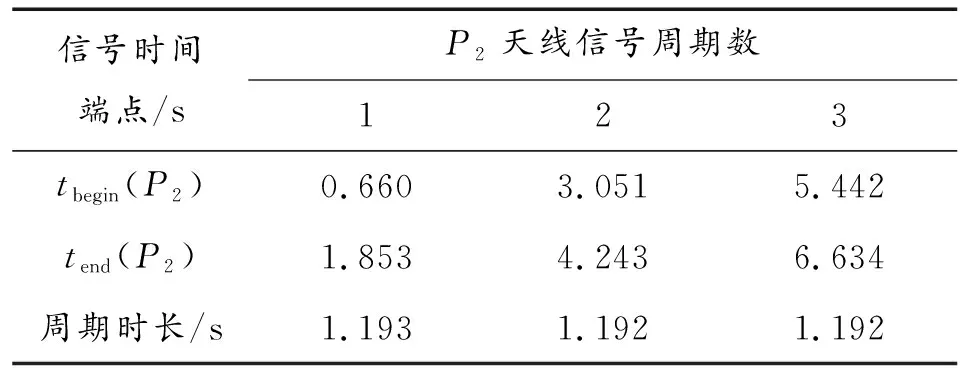
表3 单天线信号的时间端点提取结果

P2天线三个周期时长分别为：1.193 s、1.192 s、1.192 s，与所实测信号单天线周期1.199 s的相对误差均小于0.5%，可获得了较为精确的时间端点信息，完成了单天线信号的提取，证明了本文方法的有效性。

4 结论

1) 基于微多普勒阶跃端点与双天线轮序切换节点相互对应的原理，利用信号差分处理获得信号的端点信息，并通过傅里叶曲线拟合对所得信息进行平滑处理，最终提取出精确的信号时间端点，从而实现双天线信号的双路分离，为微多普勒频率阶跃的消除或处理提供了有效的信号基础；2) 本文中所涉及差分处理与曲线拟合等方法在空间信号分析与数据处理等领域也具有一定的工程实践意义与参考价值；3) 由于微多普勒的阶跃呈现为周期性规律，通过对单天线支路信号的反相处理，可实现阶跃特征的消除，或通过估计微多普勒重点参数，进一步完成所需特征的提取，这也是下一步的研究方向。