一种基于边长约束的界址点坐标平差方法

陈长波

（1.广东省国土资源测绘院，广东 广州 510500）

近年来，随着数字摄影测量技术的快速发展，全国很多地区结合自身对地理信息资源的需求，开展了高分辨率航空影像数据建设。如何将其成果应用到村庄地籍调查中，快速、高效地完成村庄地籍调查，已成为国土资源管理和地籍调查人员探讨的重点。基于高分辨率影像图解的界址点坐标[1-7]，采用坐标法计算宗地面积与实际面积存在较大差异[8]。为此，本文以图解的界址点坐标为基础，以实地丈量的界址边长及界址边方位变化最小为约束，采用附带约束的平差方法进行图解界址点坐标计算[9]，使得最终的图解界址边长与丈量界址边长一致、界址边方位角变化最小，并使用图解界址点采用坐标法计算宗地面积，满足解析法地籍调查宗地面积计算要求。

1 数学模型

1.1 界址点坐标观测值误差方程式

以图解的界址点、地物点的坐标作为观测值，由于图解坐标观测值含有误差，使得根据这些顶点的坐标计算的宗地面积与实际面积不一致。假定（xi，yi）为界址点Ji的图解坐标，相应的平差值、观测值改正值、未知参数分别为（，）、（v，v）、（δx，δy），则：xiyiii

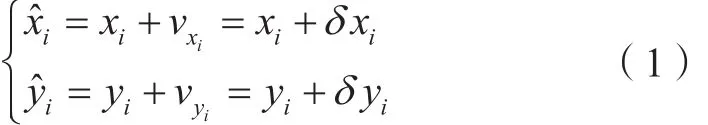
对所有界址点、地物点坐标观测值，列出误差方程如下：

式中，V1为坐标观测值改正数向量；δX为坐标未知参数向量。顾及图解坐标的精度一致性且相互独立，故观测值的权为单位阵。

1.2 界址边长约束条件方程式

对任意界址边JiJi+1，实地丈量边长为li,i+1，由于实地丈量界址边长精度高于图解界址边长，在此不考虑界址边长丈量误差影响，则有：

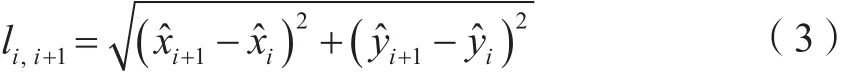
线性化，得：

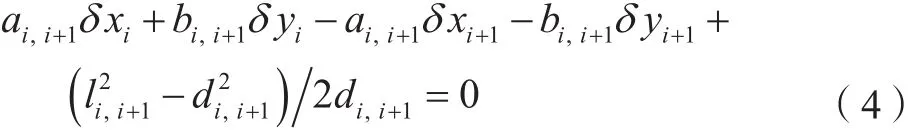
对所有界址边长（含界址点至地物点丈量距离）列立约束条件方程，得：

式中，C为约束条件方程式系数阵；W为约束条件方程式常数向量。

1.3 方位角虚拟观测值误差方程式

在实际情况中，存在界址边长不一，当界址边长差异很大时，仅利用界址边长约束进行界址点坐标平差对界址边方位影响较大，进而引起界址边夹角变化，极容易对几何图形产生扭曲变形。对于0.5 m的界址边长，当界址点坐标在垂直于界址边方向产生5 cm的改正，对界址边方向影响接近6°。为此，增加界址边方位角虚拟观测值。

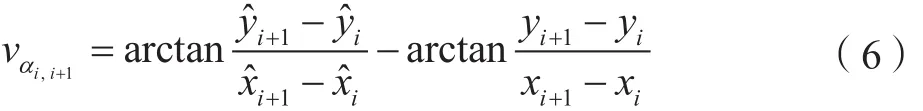
线性化，得：

对所有界址边列立方位误差方程，得：

式中，V2为界址边方位角虚拟观测值改正数向量；B为误差方差式系数阵；相应的权阵P。

1.4 误差方程式求解

联合图解坐标观测值误差方程式（2）、界址边长约束条件方程式（5）及界址边方位角虚拟观测值方程式（8），根据最小二乘原理，组成极值函数[10]：

将Ψ对δX求一阶倒导数，并令其为零，得：

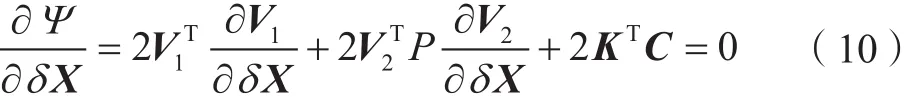
顾及式（2）、（8），得：

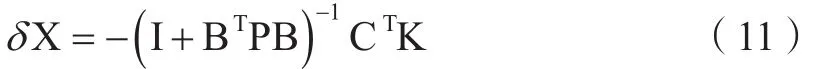
式中，I为单位阵。将式（11）代入式（5），解得：

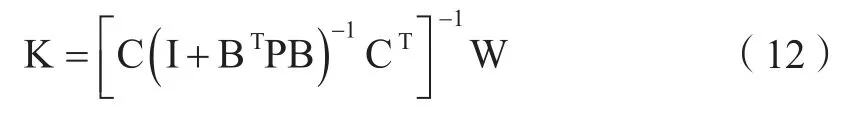
最终，解得未知参数δX。由此解得所有界址点及地物点的坐标，且所有界址边长的图解与实际丈量的一致。此时，可直接利用图解界址点平差坐标计算宗地面积：

2 算例及精度分析

2.1 单宗地计算实例分析

以图1所示的宗地为例，图解界址点坐标及外业实测界址边长分别见表1第2、3列，如图1所示。为比较界址边长差异对平差坐标的影响，分别采用仅约束界址边长、约束界址边长及方位角变化最小两种方案，分别计算了界址点的坐标，结果见表1第4、5列和第6、7列。

图1 宗地示意图及实测界址边长

表1 图解界址点坐标及平差坐标

计算结果表明，通过平差计算，最终的界址边长均与实测边长一致，即通过平差实现几何图形界址边与实际的一致对应。

采用几何要素计算本宗地面积为308 m2，分别采用图解坐标、边长约束平差坐标、边长角度约束平差坐标计算本宗地面积分别为312.965 1 m2、310.617 0 m2、308.032 1 m2，与几何要素法计算面积差分别为4.965 1 m2（相对差1.61%）、2.617 0 m2（相对差0.85%）、0.032 1 m2（相对差0.01%）。由此可见，通过约束平差，面积精度得到了显著提高。

利用界址点坐标反算界址边夹角，并与图解界址边夹角相比，其中边长约束平差界址边夹角变化最大达到1.5°，边长角度约束平差界址边夹角变化最大仅为5′，两者相差接近20倍。

由此可见，采用边长角度约束平差图解宗地界址坐标，宗地面积与实际面积差值较小，且界址边夹角变化很小，实现几何图形保真。

2.2 村庄地籍调查实例分析

图2 图解村庄示意图

为检验方法的普适性，将上述方法用于如图2所示的某村庄地籍调查。首先基于1∶2 000数字正射影像图解各宗地，共得到350宗，平均宗地面积约90 m2。而后利用外业实测界址边长及相邻宗地界址点相互位置关系，进行边长角度约束平差计算图解界址点平差坐标，并与实测宗地面积比对，结果与上述结果基本一致。

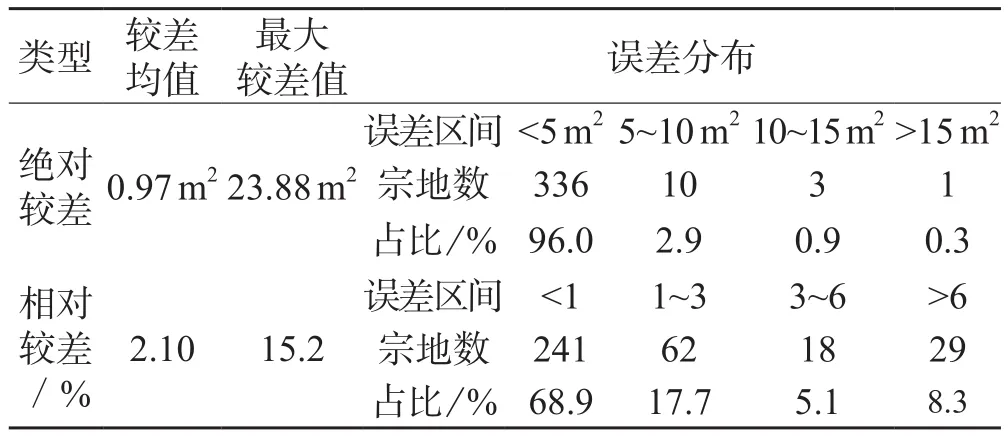
表2 计算面积与几何要素计算面积较差统计表

表2表明，采用本文的边长角度约束平差，图解面积与实测面积较差在1%范围内的约占70%，3%范围内的约占90%。个别误差较大的宗地，究其原因，主要是宗地面积过小，稍许误差即可引起较大的相对误差，当扣除小面积（此处取20m2以内），95%以上宗地相对误差在0.5%以内。因此，在实际作业中，当面积较小时（此处取20m2）应特别注意宗地面积对宗地相对误差的影响。

表3 计算方位角与图解方位角较差统计表

表3表明，边长角度约束平差坐标计算宗地界址边方位角，75%以内的方位角变化在15′内，采用边长角度约束平差图解宗地界址坐标，同样可以实现几何图形保真。

5 结 语

以图解的界址点坐标作为基础，以实地丈量的界址边长及界址边方位变化最小为约束，采用附带约束的平差方法进行图解界址点坐标改正，使用图解界址点平差坐标计算宗地面积，既解决了宗地不规则的问题，又满足了几何要素的要求。

通过村庄地籍调查实践证明，该方法既能高效便捷地开展村庄地籍调查，又能保证界址边长和宗地面积的可靠性，方法完全可行，具有很好的应用前景。