方差分量估计方法对比分析

郑 蓉 何思源

(1.中国电力工程顾问集团西北电力设计院有限公司，陕西西安 710075； 2.中铁第一勘察设计院集团有限公司，陕西西安 710043)

在进行平差处理时，必须先建立与之相应的数学模型。平差处理的数学模型由两部分组成，即函数模型和随机模型。其中，函数模型表达的是观测量与观测量之间、观测量与待估参数之间的相互关系，随机模型表达的是观测噪声的一些随机特征，这里主要指观测误差Δ的数学期望和方差

E(D)=h

(1)

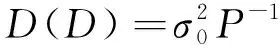
(2)

平差数据处理中，最优的参数估计和合理的精度评定都是以正确的观测值随机模型(协方差阵)为前提，方差-协方差分量估计就是确定观测值的协方差阵。采用传统的验前精度定权并不能得到合理的观测值随机模型，对参数估计也将产生影响。因此，研究方差分量估计方法在数据平差处理中具有重要的意义。

从1924年Helmert提出先利用预平差得到改正数，然后按验后方法估计各类观测量方差开始，许多学者针对方差分量估计进行了大量的研究，先后导出了著名的最小范数二次无偏估计(MINQUE)，Helmert方差分量估计的严密公式及简化的迭代算法，最优二次无偏估计(BQUE)；於宗俦导出了适用于所有平差方法的Helmert方差协方差分量估计公式、最优不变二次无偏估计公式和极大似然估计公式。由于方差分量估计算法本身的特点，其相较于平差参数的估计更为复杂，在迭代求解的过程中涉及到大量的矩阵运算，导致其在面对海量观测数据的平差处理时计算效率过低。因此，寻找一种高计算效率的近似算法显得尤为必要。

基于上述方差分量估计方法在实际应用中面临的问题，通过设计合理的实验数据，对比分析现有方差分量估计方法在计算效率和精度上的差别，以期得到相对较好的方差分量估计算法。

1 各种方差分量估计方法的比较

现有的方差分量估计方法有很多种，比较知名的有Helmert方差分量估计及其简化算法，二次无偏估计(最小范数二次无偏估计，最优不变二次无偏估计)，最小二乘方差分量估计。以下介绍各种方法的原理并对各个算法的运算效率进行比较。

1.1 方差分量估计原理

(1)Helmert方差分量估计的严密算法

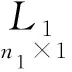
(3)

且有下列关系式

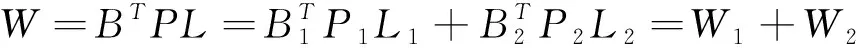
(4)

推导得到方差-协方差分量估计的通用公式为

(5)

式中

S=

公式(5)即为两类观测值情况下间接平差模型的Helmert方差分量估计公式，详细推导过程请参考文献[14]。方程组中未知参数个数与方程个数相同，具有唯一解。

(2)Helmert方差分量估计的简化算法

略去严密公式(5)中的求迹部分，则有

(6)

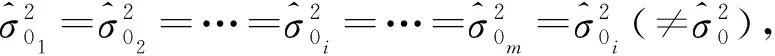
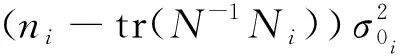
(7)

由此可得简化公式为

(8)

另外一种简化算法这里不再详细推导(可参照文献[10])。

(3)二次无偏估计

二次无偏估计的基本思路是先提出估计应该具有的性质，如：无偏性，不变性，最小范数等，再把满足这些性质所附加的条件构成一个极值问题，求解这个极值问题的解，即可得到所需的估计结果。

略去部分推导过程，这里直接给出观测向量的二次型矩阵M需要满足的极值条件

(9)

最终得到MINQUE的估计公式

(10)

式中

详细推导过程可参考文献[8]。

(4)基于最小二乘残差方程的方差分量估计

国内学者李博峰，沈云中等在Gauss-Markov模型的基础上，从最小二乘残差方程出发，建立方差分量估计的基本方程，并在给定观测值方差矩阵初值的情况下，导出了各种方差分量估计方法的公式。

基于最小二乘残差方程的Helmert方差分量估计公式为

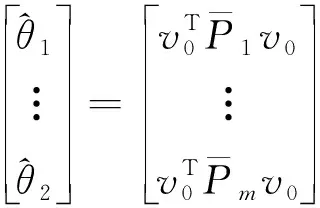
(11)

基于最小二乘残差方程的MINQUE(LS-MINQUE)公式为

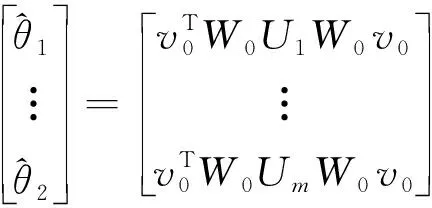
(12)

在公式(12)的基础上，推导出一种高效率的方差分量估计公式(L算法)

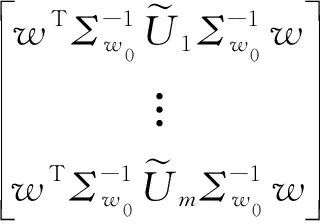
(13)

以上两种方法的详细推导过程可参考文献[7]。

1.2 最小二乘方差分量估计

最小二乘估计准则对线性模型来说具有普遍适用性，在对参数进行估计前，不需要已知其分布的任何信息，这一优越的性质使其成为目前使用最为普遍的估计准则。归庆明，黄顺玉在1996年提出过一种最小二乘方差分量估计方法，该方法利用一种行之有效的离散-均值对应方法，把随机模型的方差-协方差化为派生函数的均值参数，然后对派生模型的均值参数进行最小二乘估计，从而得到模型方差-协方差分量的最小二乘估计，其公式为

(14)

其中

yvh=vh(ttT-BTQ0B)

方差-协方差分量最小二乘估计的详细推导公式可参考文献[12]。

2 实验对比分析

2.1 实例描述

通过模拟一个边角网的观测数据，对比分析6种不同的方差分量估计算法在计算效率和精度上的差别。

如图1所示，设计一个边角网，给定P1、P2、P3、P4纵横坐标的真值(如表1所示)。由坐标真值反算出任意两点间的精确距离，以四个控制点中的任意点为测站点，反算出三个方位角精确值(如表2所示)。可得到一个多余观测最多(共6个距离，12个方位角)的大地四边形控制网数据。

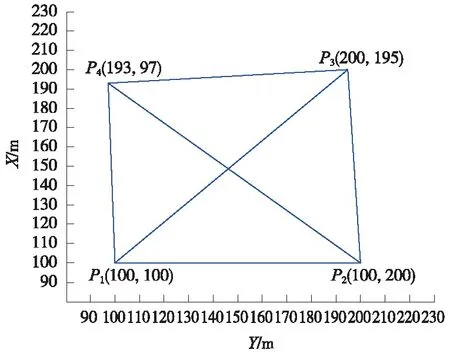
图1 模拟边角网[8]

固定P1点的横纵坐标和P2点的横坐标，另外的五个坐标待估(假设距离和方位角观测值的方差未知)。数据处理采用Matlab R2010b，模拟1 000次观测数据，每次给距离和方位角的精确值加上的期望为零，标准差分别为10 mm和2″的正态分布随机噪声。通过每一次模拟出的观测值，利用极坐标法求出P4、P3点的纵坐标和横坐标以及P2点横坐标的近似值，然后按间接平差的方法开列误差方程，进行平差计算。

表1 控制点坐标的真值

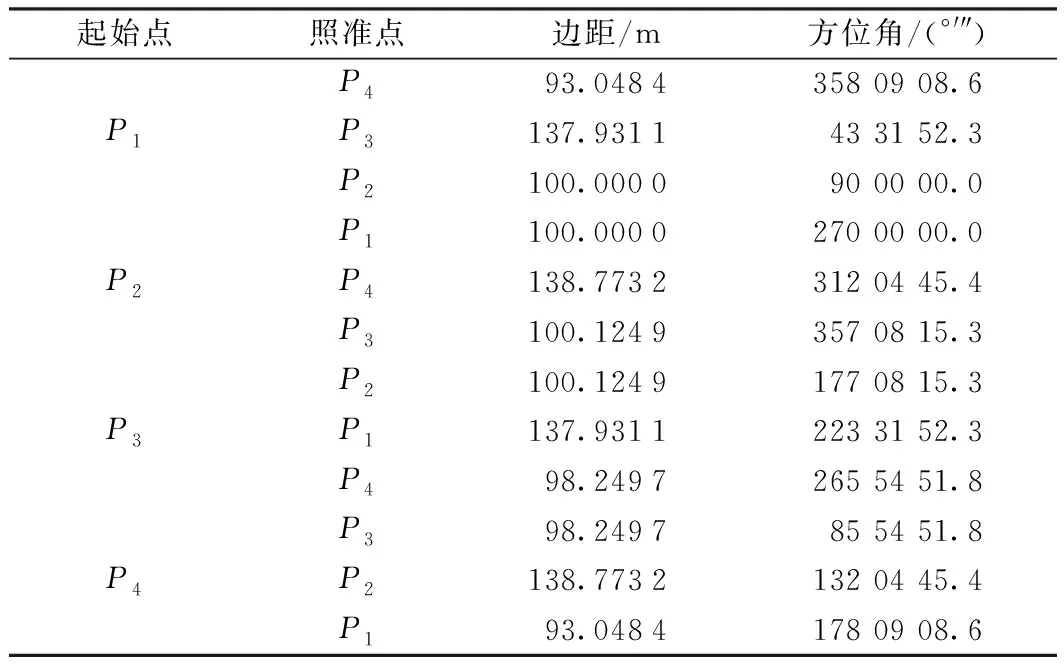
表2 模拟数据距离和方位角

2.2 不同方差分量估计算法计算结果的对比分析

为了保证所得结果的可靠性，所有算法所使用的数据都由上述实验提供，且保证计算环境(操作系统，编程语言，迭代阈值等)相同，其中迭代阈值统一选取为

(15)

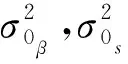
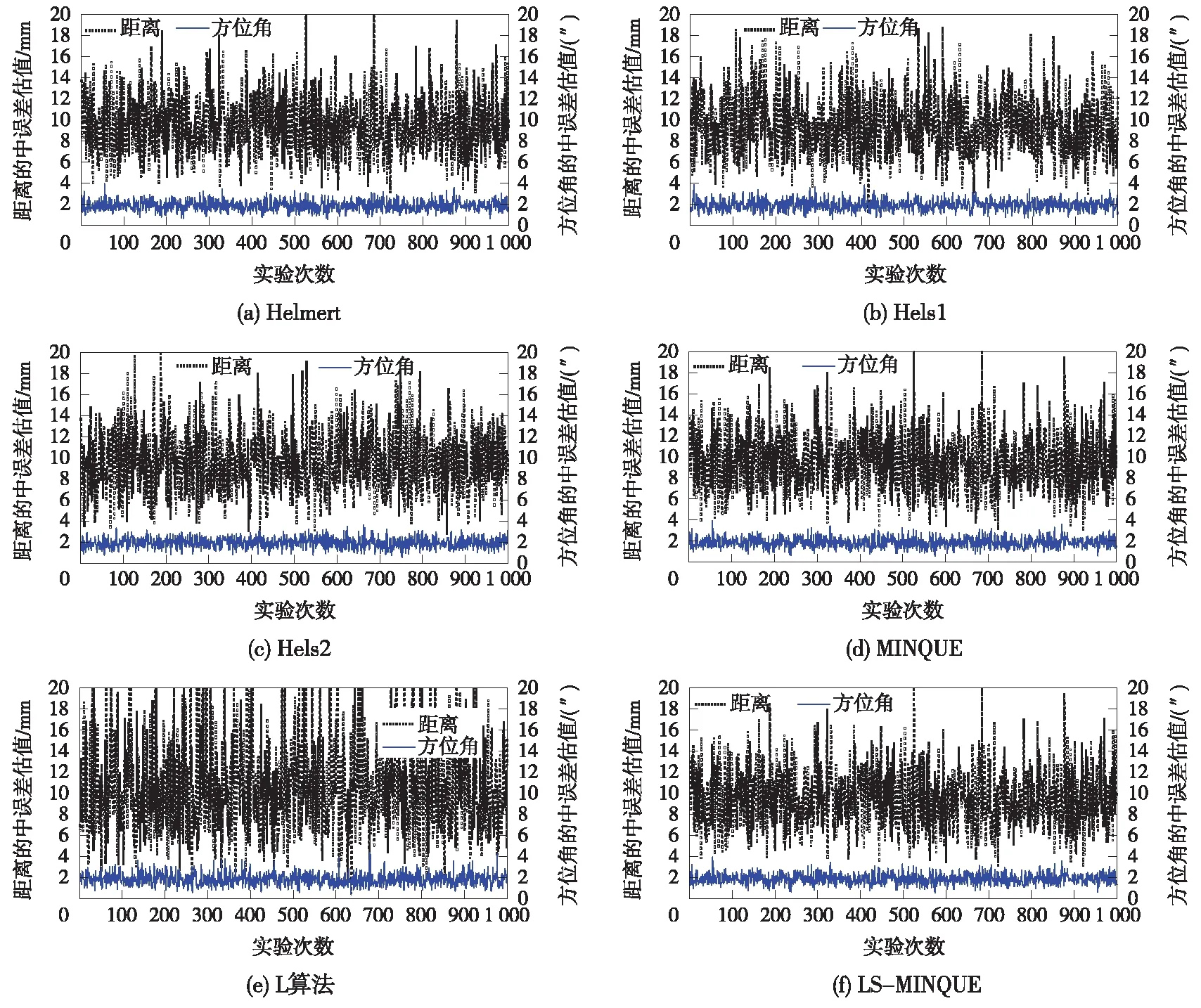
图2 6种方法统计结果

图2(a)为Helmert方差分量估计严密算法，图2(b)为Helmert方差分量估计简化算法一(Hels1)，图2(c)为Helmert方差分量估计简化算法二(Hels2)，图2(d)为MINQUE，图2(e)为L算法，图2(f)为基于最小二乘残差方程的MINQUE。

通过对比可以得到以下结论：

(1)受到有限观测数据的影响，在一次计算中方差分量的估计结果具有随机性，但从1 000次计算的统计结果来看，距离和角度的精度估值与模拟精度一致。

(2)L算法所得距离的精度估值相较于其他五种算法来说波动幅度较大，这是因为L算法相较于其他五种算法，在迭代的过程中没有平差计算的参与，由预平差得到的观测值残差在整个迭代过程中保持不变，这也就造成了L算法的估计结果会在很大程度上依赖于所选初值的大小。

(3)距离观测值中误差的离散度要比方位角观测值中误差的离散度大，这是因为方位角(12个)的多余观测多于距离(6个)，这也证明了多余观测数越多，方差分量的估计结果越稳定。

2.3 不同方差分量估计算法计算效率的对比分析

在统计每一种算法所用时间时，所用的模拟数据是相同的。计算时间的始点均为进入迭代运算的循环开始处，终点均为达到迭代阈值条件后跳出迭代运算的循环结束处。所有算法的计算环境、迭代阈值以及给定的初值完全相同。

图3为6种算法所用时间的统计结果(单位为10-4s)，横轴为实验次数，表3是对耗时的统计结果。可以明显看出，Hels2所用时间最短，其次为Hels1，Helmert严密算法和MINQUE所用时间大致相同，L算法和基于最小二乘残差方程的MINQUE所用时间最长。

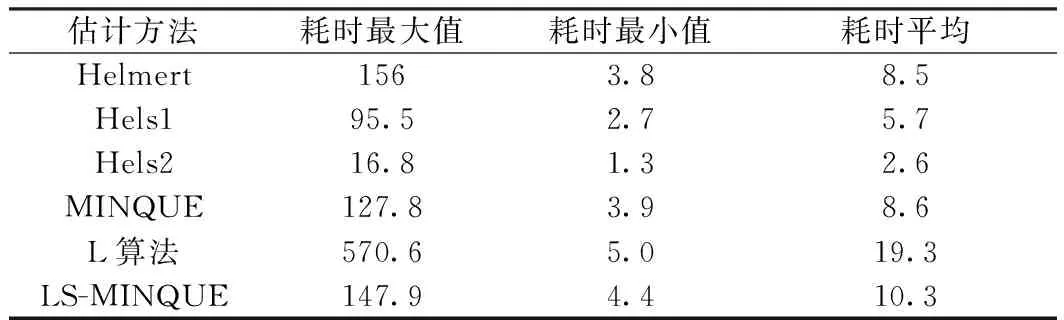
表3 计算时间统计 10-4s

为了更精确地反映不同算法的计算效率，这里定义计算时间的提高率为

p=(t1-t2)/t1×100%

(16)

式中，t1，t2分别为两种方差分量估计算法所用时间。

为了寻找一种精确高效的方差分量估计方法，故这里只以计算所用时间最短的Hels2为研究对象，给出其相较于两种经典的方差分量估计方法计算时间提高率的统计结果，从计算结果来看，Hels2相对于Helmert严密算法和MINQUE的计算时间提高率为55%～75%(如表4)。

表4 计算时间提高率统计

3 结束语

通过实例验证，Helmert方差分量估计的第二种简化算法(Hels2)相较于Helmert严密算法、Helmert的第一种简化算法(Hels1)、MINQUE、基于最小二乘残差方程的MINQUE以及L算法[8]，在迭代阈值满足式(14)的情况下，具有最高的计算效率；相较于Helmert严密算法和MINQUE，计算时间提高率为55%～75%，且在计算精度上与其等效，故可以采用Hels2替代其他算法，以满足对方差分量估计计算效率的要求。