GM(1，1)模型在巨型溶洞超厚回填 路基沉降监测中的应用

陈 健

(中铁第四勘察设计院集团有限公司，湖北武汉 430063)

为了保证线路的平顺性和稳定性，线下工程的沉降监测在建设期间和运营期间都是一项重要工作内容。为应对新时期铁路工程建设的需要，中国铁路总公司于2016年7月发布了《铁路工程沉降变形观测与评估技术规程》，对速度200 km/h及以上有砟轨道的沉降观测有了明确要求和规定，其中软土、松软土、高填方路基及过渡段等易发生工程地质灾害的位置是沉降变形监测工作关注的重点[1，2]。

在隧道工程的施工过程中，溶岩发育的地段会遇到穿越巨型溶洞的特殊状况，此时，回填处理是一项较为常见的处理措施。由于巨型溶洞的特殊地形和地质构造，会形成一段超厚回填路基。在铁路运营期，在自然沉降与列车动荷载的作用下，常出现路基的整体或局部沉陷，特别是过渡段的沉陷尤为突出[3，4]，路基的工后沉降也将十分明显。影响超厚回填路基稳定的因素复杂且多样，为了保证溶洞处理后铁路的正常运营，需在路基填筑过程中及填筑完成后进行沉降监测，掌握其沉降规律，为后续施工措施提供指导。

GM(1，1)模型在变形监测领域应用非常广泛。黄红军、曹凯等研究了GM(1，1)模型在建筑物沉降监测中的应用[5，6]，李晓红、姚颖康等研究了GM(1，1)模型在滑坡监测中的应用[7，8]，王在诚、林飞等研究了GM(1，1)模型在路基沉降观测中的应用[9，10]。这些都是针对常规变形监测项目的研究，鲜有针对巨型溶洞超厚回填路基这种极端地质条件下的应用研究。因此，研究GM(1，1)模型在极端条件下的应用，对于工程建设经验的积累具有一定的实用价值。

在介绍GM(1，1)模型预测法原理和精度评定的基础上，依托新建黔张常铁路高山隧道巨型溶洞超厚回填路基沉降监测和预报项目，根据监测点累计沉降量的变化关系建立GM(1，1)模型，对所得模型的精度进行评定，并利用该模型对该段超厚回填路基的累计沉降量和沉降趋势进行预测，将预测结果与设计预想和现场实际情况进行对比，综合判断GM(1，1)模型的适用性。

1 GM(1，1)模型预测法原理及其精度评定

灰色理论一般模型为GM(m，n)模型，即n个变量的m阶方程，m和n的不同取值决定了不同的模型。灰色理论的主要内涵是在信息贫乏系统的部分已知信息中提取出能够对系统的运行规律进行正确描述的有价值信息[11]。GM(1，1)模型是灰色理论中最简单而又最重要的一种模型。

1.1 GM(1，1)模型预测原理

适用于GM(1，1)模型的数列需为非负、离散、等时距数列，若需参与建模的数列为非等时距序列，则可采用线性差值的方法对原始数列进行处理，转换成等时距数列。

设x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}为一非负、离散、等时距数列，数列长度为n，对x(0)进行一次累加，生成一新数列

x(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}

(1)

利用此新数列建立一阶微分方程[12]

(2)

根据最小二乘法解算GM(1，1)模型的系数[13]

(3)

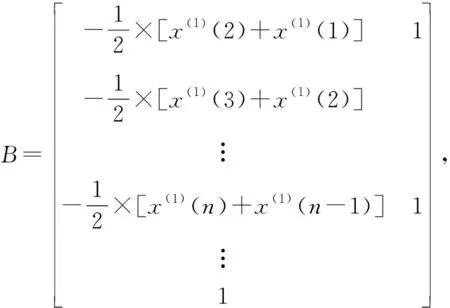
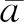
(4)

(5)

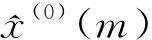
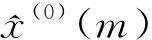
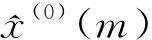
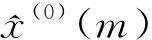
1.2 GM(1，1)模型精度评定

通常用后验差方法对GM(1，1)模型的精度进行评定。后验差比值C、小误差概率P这两个参数是评定模型精度的主要指标，具体求解步骤如下。

步骤1：利用x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，由GM(1，1)模型得到

(6)

计算残差

(7)

步骤2：求解原始数列的平均值，可得

(8)

步骤3：求解残差的平均值，可得

(9)

步骤4：求解原始数列的均方差

(10)

步骤5：求解残差的均方差

(11)

步骤6：得到后验差指标

C=S2/S1

(12)

P={|b(m)|<0.674 5S1}

(13)

后验差比值C小说明虽然原始数据较离散，但残差离散程度小，小误差概率P大说明该模型预测的精度比较高，所以C值越小越好，P值越大越好[14，15]。

2 巨型溶洞超厚回填路基沉降监测实例

新建黔张常铁路Ⅳ标高山隧道属于岩溶强烈发育区域，为Ⅰ级风险隧道。在开挖过程中发现一个巨大的厅堂状溶洞，长约100 m，宽32～63 m，高46～65 m，溶洞底板自线路左侧向右侧约呈13°向下倾斜，在溶洞南端尽头又以裂隙型溶洞继续向远离线路方向左右侧延伸，洞底堆积物以粉质黏土为主，夹少量角砾，层厚5～10 m，局部大于10 m。线路斜穿溶洞而过。设计采用回填的方式对溶洞的空腔进行处理，进而形成了一段超厚回填路基，回填的材料主要有掺5%水泥级配碎石、加工洞砟、普通洞砟。该段超厚回填路基填土地基高度为30～55 m，洞底充填体高度为37～66 m，预计工后沉降将十分明显。为保证溶洞在处理过程中的安全及铁路运营安全，需进行严密的沉降监测。

由设计资料可知，溶洞洞壁及洞顶存在塌落掉块风险，稳定性较差。因此，在布设沉降观测基准网时，需选择稳定可靠的位置埋设基准点。根据设计单位勘察资料，在洞壁较为稳定的岩石及平导水泥支撑层上选择了3处(植入不锈钢观测标)作为沉降监测网的基准点，基准点的高程成果通过与整个隧道的高程控制网联测并经严密平差求得。路基顶面的沉降观测点埋设于填筑层顶面。基准网采用二等水准测设，监测网首期数据采集采用二等水准往返测，从第二期开始采用单程附合水准路线观测。该段超厚回填路基的测点布设和水准观测路线示意如图1所示。

图1 测点布设图和水准路线示意

此处选取某一监测断面的3个监测点在路基填筑完成至施工加强混凝土底板之间的沉降观测期及路基加固处理期的9期沉降观测数据，对观测数据进行处理后，累计沉降量统计如表1所示。

表1 某断面监测点累计沉降量 mm

由表1的数据采集时间可以看出，监测点数据的监测频次为3天1次，所选取的9期数据构成的数列是一个非负、离散、等时距数列，无需进行转换处理，满足GM(1，1)建模要求。

3 工程实例建模计算过程及预测结果分析

以实例中7号、8号和9号监测点的9期累计沉降量数据作为原始数据用于GM(1，1)建模，此处以8号监测点为例详述建模过程，以8号监测点累计沉降量构建原始数列

x(0)(m)={10.1，16.4，22.2，28.2，34.1，39.8，45.9，52.9，59.6}；

据此原始数列构建新的累加生成数列

x(1)(m)={10.1，26.5，48.7，76.9，111.0，150.8，196.7，249.6，309.2 };

构建数据矩阵B和数据向量

采用与8号监测点同样的建模方法可得到7号监测点的沉降预测模型

同样可得到9号监测点的沉降预测模型

GM(1，1)模型的模拟值与监测值的较差情况(即残差)以及模拟值所呈现的变化趋势是否与监测值变化趋势一致能够反映出模型的拟合效果，本实例中GM(1，1)模型的具体拟合情况如表2和图2～图4所示。

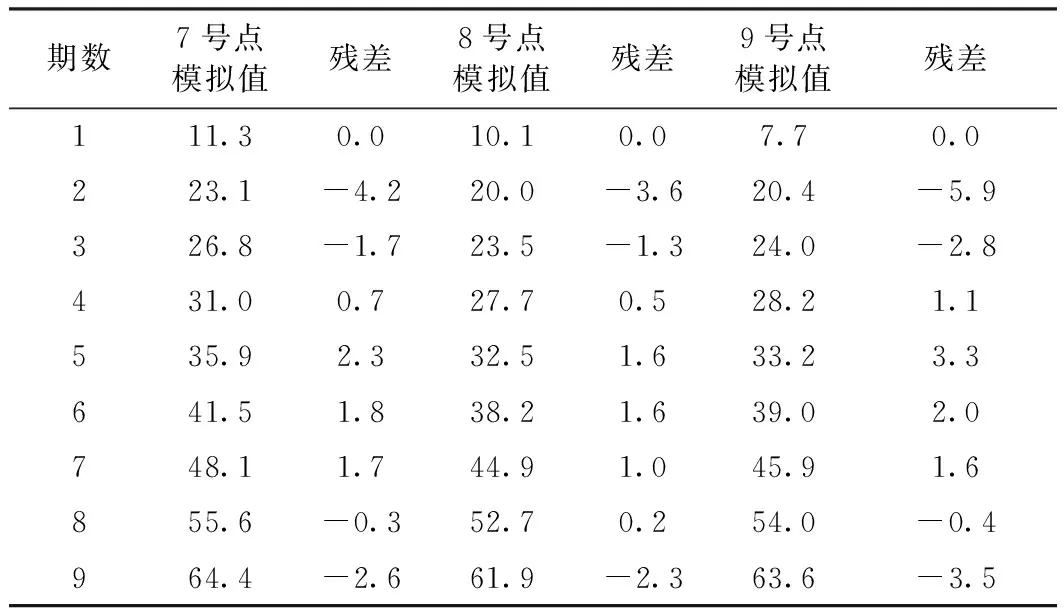
表2 高程监测值与模型模拟值较差 mm

图2 7号点GM(1，1)模型模拟效果

图3 8号点GM(1，1)模型模拟效果

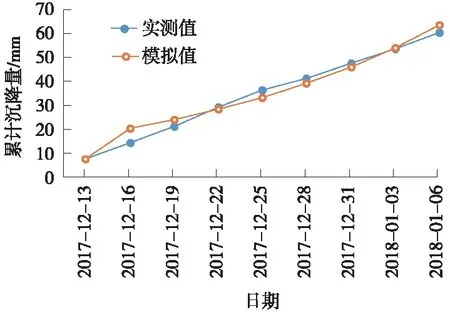
图4 9号点GM(1，1)模型模拟效果

根据表2中累计沉降量的拟合情况，由8号点的GM(1，1)模型计算可知：S1=15.778 1，S2=1.714 0，得到8号点GM(1，1)模型的后验差比值C=0.108 6，小误差概率P=1，根据预测模型精度等级划分，其拟合精度达到Ⅰ级。同样可以计算出7号点和9号点模型的精度指标，如表3所示。

由预测模型可以预测后3期累计沉降量的预测值(如表4所示)。

表3 模型精度指标

表4 累计沉降量预测值 mm

由表2和图2～图4可知，3个监测点的累计沉降量逐渐增加，监测值与模拟值的残差较小且该监测点的实际沉降趋势与表4中体现的预测趋势吻合情况良好，该监测点仍呈下沉趋势。按照以上建模过程和方法对所有的监测点数据进行建模计算，即可掌握路基的整体沉降情况。

超厚回填路基的稳定性不仅与填土高度有关，还与地基的属性、填料的性质、路基压实方法等有关[16，17]。由于洞砟回填厚度大，实际填筑压实度可能达不到预想要求，为避免因沉降问题对上部隧道结构产生不利影响，根据设计要求，对本段超厚回填路基采取注浆等工程措施，以加强该回填路基的稳定性。

GM(1，1)模型在此实例中的的预测情况与设计预想情况基本一致，证明了采取后续施工加固措施的必要性，分析预测结果为后续的施工组织提供了较为有价值的参考。在后续的施工及铁路运营过程中，应持续对该路基进行沉降监测，及时进行数据的处理和分析，利用预测模型对路基的沉降情况进行预测预报。

4 结论

(1)对该巨型溶洞超厚回填路基沉降监测数据进行处理与分析，根据累计沉降量的变化关系建立的GM(1，1)模型能够较好地预测该段超厚回填路基的沉降情况，拟合精度满足实际需要，表明该模型对于岩溶发育地段超厚回填路基的沉降监测与预报适用性良好。

(2)影响超厚回填路基稳定性的因素较多，其沉降是一个动态的变化过程，应及时补充最新观测数据，提高预测精度，从而更好地反应该超厚回填路基的沉降变化趋势。

(3)GM(1，1)模型在此巨型溶洞超厚回填路基沉降监测项目中的应用方法可供类似沉降变形监测项目参考和借鉴。