燕山北部丘陵温热区ET0估算方法比较及修正

2018-08-29郝春雷张丽妍边丽梅孟繁盛慈艳华霍剑锋

节水灌溉 2018年8期

张昊，郝春雷，董喆，郑伟，张丽妍，边丽梅，孟繁盛，慈艳华，霍剑锋

(赤峰市农牧科学研究院，内蒙古赤峰 024031)

参考作物需水量(ET0)是影响作物需水量的关键因素，是灌溉决策、灌溉预报、水资源规划、农业水资源开发的基础[1-4]。因此，准确估算参考作物需水量ET0可以有效地提高作物水分利用率、灌溉预报模型的精度，在指导农田灌溉等方面具有重要意义，也一直是国内外研究的热点[5-9,11-13]。

目前，参考作物需水量计算的唯一标准方法为联合国粮农组织(FAO)推荐的Penman-Monteith公式[10]。该公式需要的基本气象参数有最高温度、最低温度、相对湿度、平均风速和日照时数，实际中常因缺乏完备的气象资料而难以被广泛应用。相比之下，所需气象资料简单的Hargreaves公式、McCloud公式、Thornthwaite公式以及P-M公式中部分指标的替代算法等受到广泛关注。刘战东等[11]根据黄淮海地区7个气象站的资料，利用FAO推荐的Penman-Monteith公式对3种基于温度的计算方法进行比较分析，得出Hargreaves与Penman-Monteith公式吻合最好，并对Hargreaves公式进行了修正。陶国通等[12]利用新乡市1970-2010年的气象数据对Hargreaves公式和McCloud公式进行了订正，筛选出Hargreaves公式作为参考作物需水量ET0的估算方法，并建立了基于温度的作物需水量计算模型。谢源泉等[13]以川东南稻区6个气象站气象数据为基础，利用FAO推荐的Penman-Monteith公式计算再生稻作物需水量，分析了川东南地区再生稻再生芽萌发期降水适宜程度的时空变异。申孝军等[4]利用石河子垦区气象资料确定了基于Hargreaves公式计算参考作物需水量的基本参数，在此基础上构建了石河子垦区膜下滴灌棉田实时灌溉预报模型。

燕山北部丘陵温热区是内蒙古自治区的粮食主产区，玉米、杂粮、杂豆等在该区域均大面积种植，尤其以玉米种植面积居多，但生产上面临一系列的限制因素制约该地区的农业发展，尤其是水资源的不足与作物生长需水不匹配。而在该区域参考作物需水量的估算方法及修正等方面的研究鲜有报道，鉴此，本文根据该区域已有气象资料，对ET0估算方法的应用效果进行初步评价，筛选出不同时间尺度既有一定预测精度而且能够在气象资料不足的情况下准确的估算ET0，以期为实时灌溉预报模型、田间水分管理以及灌溉水的高效利用提供理论指导和技术支持。

1 材料与方法

1.1 数据来源

本研究选取赤峰气象站1981-2014年的逐日气象数据，包括最高气温(℃)、最低气温(℃)、相对湿度(%)、平均风速(m/s)和日照时数(h)等，以上气象数据均来自中国气象科学数据共享服务网(http:∥data.cma.cn/)。利用FAO推荐的Penman-Monteith(P-M)公式为标准，以Hargreaves(Harg)公式、McCloud(Mc)公式、Irmark-Allen(I-A)公式为对照，计算日、旬、月3种时间尺度的ET0值(ET0旬值和月值均由逐日的ET0值统计而来)。各计算方法基本公式如下。

1.2 研究方法

1.2.1 ET0的估算方法

1.2.1.1 Penman-Monteith公式(P-M公式)法

PM公式计算的是假设作物高度为0.12 m、并且有固定的地表阻力(γ=70 s/m)和反射率(α=0.23)的假想参考作物需水量，相当于高度均一、生长旺盛、完全覆盖地面并不缺水的开阔绿草地的需水量。其计算公式为：

式中：ET0为参考作物需水量，mm/d；Rn为作物冠层表面的净辐射量，MJ/(m2·d)；G为土壤热通量日总量，MJ/(m2·d)；T为空气平均温度，℃；u2为2m高度处日平均风速，m/s；es为空气饱和水汽压，kPa；ea为空气实际水汽压，kPa；Δ为饱和水汽压与空气温度关系曲线的斜率，kPa/℃；γ为湿度计常数，kPa/℃。

公式中各参数计算方法如下：

(8)

ωs=arcos[-tan(φ)tan(δ)]

(11)

式中：Z为海拔高度，m；uh为离地面hm高出的风速，m/s；e0(Tnax)和e0(Tmin)分别表示空气温度为Tmax、Tmin时的饱和水汽压，kPa；RHmean为空气平均相对湿度；GSc为太阳常数=0.082MJ/(m2·min)；dr为地球和太阳相对距离的倒数；δ为太阳的磁偏角，rad；ωs为太阳时角，rad；φ为地理纬度，rad；J为一年中的第几天；N为日照时间，h；as和bs为修正系数，在计算中一般取as=0.25和bs=0.5；Tmax,K和Tmin,K分别为最大、最小绝对温度K(K=℃+273.16)；σ为Stefan-Boltzmann常数=4.93×10-9MJ/(K4·m2·d)；Rns、Rnl、Ra、Rs、Rsa分别为净短波辐射、净长波辐射、大气顶层辐射、短波辐射、晴空太阳辐射，MJ/(m2·d)。

1.2.1.2Hargreaves公式法

Hargreaves和Allen在1985年建立了Hargreaves公式，该公式只需要最高气温和最低气温以及大气层顶辐射就可计算参考作物需水量。Hargreaves公式为最常用的以气温数据为输入的ET0计算公式。其计算公式为：

式中：ET0为参考作物需水量，mm·d；Ra为大气顶层辐射，MJ/(m2·d)；λ 为水汽化潜热，其值为2.45MJ/kg；Tmax为日最高气温，℃；Tmin为日最低气温，℃；K为转换系数，建议值为0.002 3；n为指数系数，建议值为0.5；Toff为温度偏移量，建议值为17.8。

1.2.1.3McCloud公式法

该公式基于日平均气温，视ET0为温度的指数函数，公式如下式所示：

ET0(Mc)=KW1.8Tmean

(18)

式中：ET0(Mc)为用McCloud公式计算得到的ET0，mm/d；Tmean为平均气温，℃；其中，K=0.254，W=1.07。

1.2.1.4Irmark-Allen公式法

Irmark-Allen(I-A)公式是由Irmark等[15]在2003年提出的基于温度与净辐射计算ET0的方法，公式如下式所示：

ET0(IA)=0.489+0.289Rn+0.002 3Tmean

(19)

式中：ET0(IA)为用Irmark-Allen(I-A)法计算得到的ET0，mm/d；Tmean为平均气温，℃；Rn为作物冠层表面的净辐射量，MJ/(m2·d)。

1.2.2 数据分析及精度评价指标

采用SPSS22.0和Excel2016对数据进行分析处理。

除了通过图形直观分析外，还利用平均偏差、平均相对偏差、相关系数评价3种ET0估算方法与P-M公式的吻合程度。

2 结果与分析

2.1 参考作物需水量ET0估算方法的比较

2.1.1ET0日值序列比较

由图1可以看出，I-A公式、Harg公式与P-M公式的ET0逐日变化趋势基本一致，均呈逐渐上升的趋势，在达到峰值后开始下降，二者基本与P-M公式保持同步。I-A公式计算的ET0值前期高于P-M公式计算值，一段时间之后低于P-M公式的计算值；Harg公式计算的ET0值整体上低于P-M公式计算值；Mc公式与P-M公式变化趋势差异较大，Mc公式计算的ET0值与P-M公式存在明显偏差，尤其是峰值滞后于P-M公式。

图1 3种ET0估算方法与PM法ET0逐日变化比较Fig.1 Comparison of daily change by PM method and 3 methods for estimating ET0

2.1.2ET0旬值序列比较

由图2可以看出，I-A公式、Harg公式与P-M公式的ET0逐旬变化趋势基本一致，均是由第一旬逐渐增加，达到峰值后然后逐渐减小，二者基本与P-M公式保持同步。Harg公式与P-M公式在第15旬达到最大值，I-A公式在第21旬达到最大值，而Mc公式与P-M公式变化趋势差异较大，Mc公式计算的ET0值与P-M公式存在明显偏差，尤其是峰值滞后于P-M公式，在第21旬达到最大，Mc公式计算的ET0的峰值与最高温度出现的旬序相一致。

不同ET0计算方法各旬对应均值的绝对偏差与相对偏差分析表明，I-A公式、Harg公式、Mc公式与P-M公式的平均偏差在夏季偏大，其他季节尤其是冬季则偏小，即平均偏差有随气温增高(降低)而增大(减小)的趋势。I-A公式计算的第1～9旬和32～36旬的ET0值比P-M公式计算的各旬的ET0偏高，偏高0.147～5.585mm(或1.4%～58%)。其余各旬偏低，偏低1.094～11.17mm(或2.8%～19%)。Harg公式计算的各旬的值比P-M公式计算的各旬的值均偏低，偏低0.007～12.73mm(或0.1%～29.3%)。第20～22旬的Mc公式计算的各旬的ET0值比P-M公式计算的各旬的ET0值偏高0.3～3.75mm(或0.64%～7.31%)，其余各旬比P-M公式计算值偏低5.06～31.86mm(或4.4%～89.6%)。Mc公式与P-M公式的偏离趋势十分明显，其与P-M公式的平均偏差和相对平均偏差均大于I-A公式和Harg公式。

相关分析显示，整体上，3种ET0估算方法的旬值序列与P-M公式存在一定相关性。各旬Harg公式、I-A公式与P-M公式的相关性明显优于Mc公式与P-M公式的相关性，即Harg公式和I-A公式与P-M公式的相关系数较大，分别为0.995、0.985和0.844。

图2 3种ET0估算方法与PM法ET0逐旬变化比较Fig.2 Comparison of ten days change by PM method and 3 methods for estimating ET0

2.1.3ET0月值序列比较

由图3可以看出，I-A公式和Harg公式与P-M公式ET0逐月均值变化趋势基本一致，均是从1月份逐渐增加，到达峰值后逐渐减小，二者基本与P-M公式保持同步，I-A公式在7月份达到最大值，Harg公式在6月份达到最大值，P-M公式在5月份达到最大值。而Mc公式与P-M公式存在明显偏差，峰值明显滞后于P-M公式，在7月份达到最大值，与最高温度出现的月份一致。

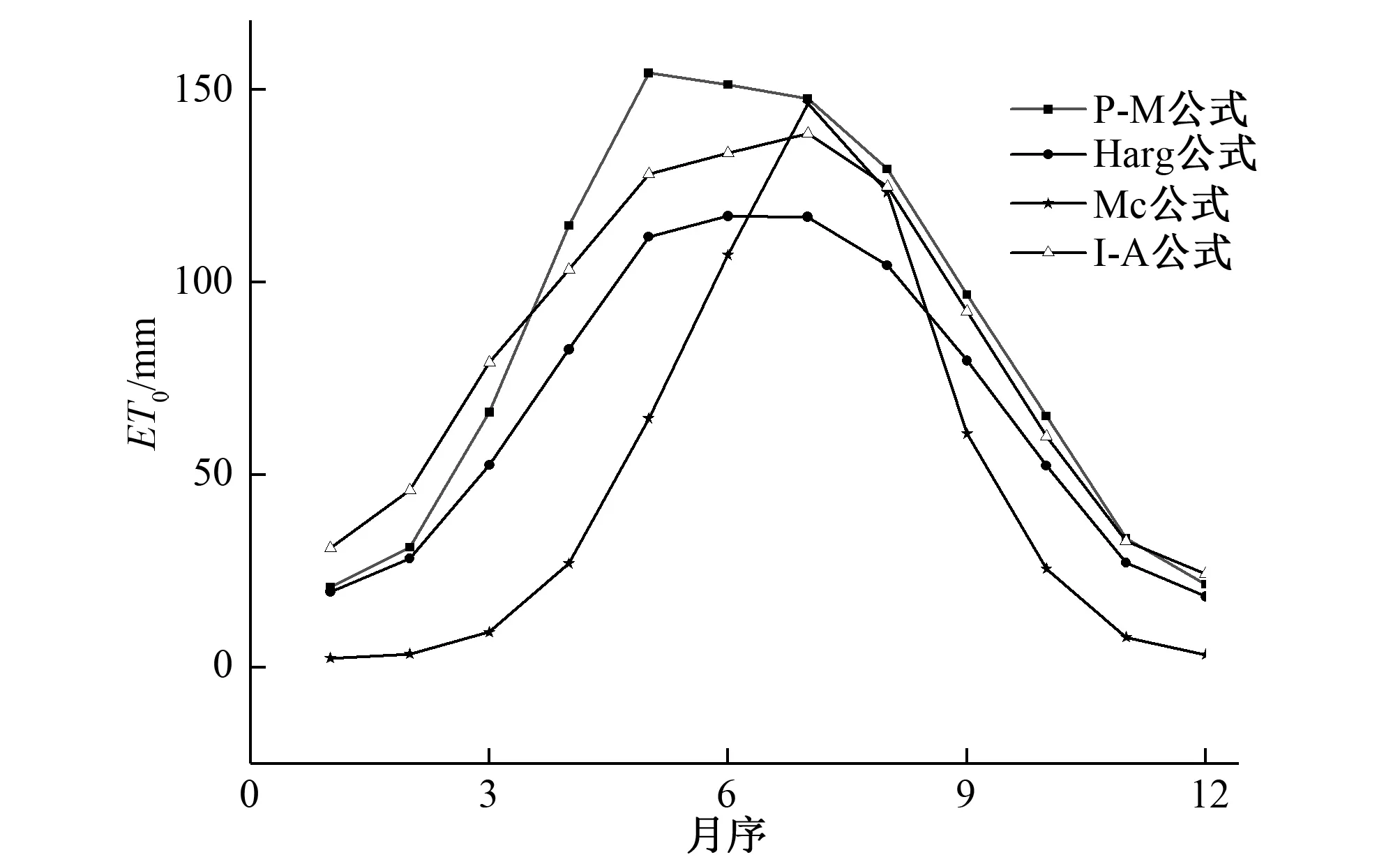
图3 3种ET0估算方法与PM法ET0逐月变化比较Fig.3 Comparison of monthly change by PM method and 3 methods for estimating ET0

不同ET0计算方法各月对应均值的绝对偏差与相对偏差分析表明，I-A公式、Harg公式和Mc公式与P-M公式的平均偏差在夏季偏大，其他季节尤其是冬季则偏小，即平均偏差有随气温增高(降低)而增大(减小)的趋势。I-A公式计算的第1-3月和12月ET0值比P-M公式计算的ET0值均偏高，偏高2.69～14.82mm(或12.54%～49.09%)，其余各月计算的ET0值均偏低，偏低0.62～26.19mm(或1.86%～16.98%)。Harg公式计算的各月的ET0值比P-M公式计算的各月的ET0值均偏低，偏低1.11～42.25mm(或5.35%～27.86%)。Mc公式计算的各月的ET0值比P-M公式计算的各月的ET0值偏低1.09～89.38mm(或0.74%～88.86%)。Mc公式与P-M公式的偏离趋势非常明显，其与P-M公式的平均偏差和相对平均偏差均大于I-A公式和Harg公式。

相关分析显示，整体上，3种ET0估算方法的月值序列与P-M公式存在一定相关性。各月Harg公式、I-A公式与P-M公式的相关性明显优于Mc公式与P-M公式的相关性，即Harg公式、I-A公式与P-M公式的相关系数较大，分别为0.996、0.986、0.851。

综上所述，在估算ET0的所有方法中，I-A公式和Harg公式表现最好，Mc公式表现最差。因此，在气象资料缺乏条件下，优先选用I-A法和Harg法。另外，不同时间尺度相关分析显示，Harg公式和I-A公式与P-M公式显著相关，相关系数最高，据此可进一步对2个公式进行修正，以提高估算精度。

2.2 公式的修正

I-A公式和Harg公式在该地区计算得到的ET0总体表现不错，但在总量和季节分配上仍与P-M公式计算结果存在一定偏差，因此可采用一定的方法对二者的计算结果进行修正使其更符合实际情况，本文采取回归修正法对公式(17)和公式(19)的内部参数进行修正。

以赤峰气象站1981-2014年逐日的最高气温，最低气温，大气顶层辐射为自变量，P-M公式计算的逐日ET0为因变量，将Harg公式原参数K=0.002 3，n=0.5，Toff=17.8作为初始值，对Harg公式进行非线性回归分析，迭代若干次后得到不同时间尺度下新的参数拟合值。

Irmark-Alleen法中ET0是平均气温和作物冠层表面的净辐射量的一次线性函数，以赤峰气象站1981-2014年逐日的平均气温和作物冠层表面的净辐射量为自变量，P-M公式计算的逐日ET0为因变量，进行线性回归分析，对I-A公式中的系数加以改进，得到不同时间尺度下新的参数拟合值，以提高计算精度，公式如式(20)所示：

ET0(IA)=a+b Rn+c Tmean

(20)

利用式(2)、式(5)和表1中的相关参数模拟赤峰市1981-2014年平均逐日、逐旬、逐月的ET0，并利用P-M公式根据气象资料计算同时段的。I-A公式的逐日模拟值与P-M公式计算值的相对偏差的最大值、最小值和平均值分别为42.2%、0.1%和11.2%；逐旬模拟值与P-M公式计算值的相对偏差的最大值、最小值和平均值分别为33.9%、0.3%和11.3%；逐月模拟值与P-M公式计算值的相对偏差的最大值、最小值和平均值分别为29.8%、1.8%和10.7%。Harg公式的逐日模拟值与P-M公式计算值的相对偏差的最大值、最小值和平均值分别为29.2%、0.002%和5.8%；逐旬模拟值与P-M公式计算值的相对偏差的最大值、最小值和平均值分别为25.1%、0.1%和6.6%；逐月模拟值与P-M公式计算值的相对偏差的最大值、最小值和平均值分别为15.6%、0.8%和7.4%。由此可见，2个公式，Harg公式的模拟效果最好，最能准确的估算燕山北部丘陵温热区的ET0，同时达到利用较少数据得到较高精度的ET0。

3 结论与讨论

在燕山北部丘陵温热区，无论日值、旬值还是月值，在上述3种ET0估算方法中，以Harg公式和I-A公式估算该地区ET0的效果较好，考虑到估算地区的实际情况，通过进一步对Harg公式和I-A公式进行修正，得出Harg公式与P-M公式的计算值最为接近，可以作为燕山北部丘陵温热区气象资料缺乏条件下计算ET0的方法，同时以Harg公式为基础，还可以建立适宜该区域的基于气象信息的实时灌溉预报模型，以提高水资源利用率，做到因需灌水，从而最大程度的控制与减轻干旱对该区域农业生产的影响。