基于果蝇优化算法的三维LED光源阵列优化设计
2018-08-28文尚胜唐浩洲钟惠婷康丽娟
何 果,文尚胜,2,符 民,2,唐浩洲,钟惠婷,康丽娟
(1.华南理工大学材料科学与工程学院,广东广州 510640;2.华南理工大学发光材料与器件国家重点实验室,广东广州 510640;3.华南理工大学聚合物新型成型装备国家工程研究中心,广东广州 510640;4.华南师范大学美术学院,广东广州 510631)
1 引 言
对比传统光源,LED有着安全环保、寿命长、污染低、耗电量少且体积小等显著优点,如今已广泛地应用于植物照明[1]、可见光通信[2]、太阳光模拟[3]、汽车前照灯[4]、隧道照明[5]等领域,在现代生活中起到重要作用。单个LED芯片的功率不足以满足照明光源的要求,因此许多照明系统是由多芯片 LED阵列集成的,以满足照明要求[6]。作为半导体照明器件,LED芯片具有显著的发光指向性,其发出的光强近似朗伯分布[7]。传统光学设计包括一次光学设计[8]与二次光学设计[9]。一次光学设计一般在LED芯片封装时进行,使灯具满足一定照明效果。二次光学设计主要是LED阵列设计,未经优化的LED阵列发出的光直接入射到接收平面上,难以得到均匀的光照效果,因此对多芯片LED阵列出光的光强均匀化设计具有极大的研究价值。现有的关于LED阵列优化大多为对平面LED阵列或曲面阵列的优化。如王加文在文献[10]提出的利用模拟退火算法对平面LED阵的照度均匀度进行优化,以及陈浩伟在文献[11]中设计的一款应用自由曲面底板的红蓝 LED植物照明用灯具。果蝇优化算法作为一种全局优化的算法,广泛应用于如气化参数优化[12]、交通运输定位[13]、供应链网络配置[14]等领域,具有原理易懂、调节方便等优势,本文拟使用果蝇优化算法对LED阵列芯片位置参数进行三维空间内的优化。
本文采用Ivan Moreno提出的一种LED阵列二维设计与优化方法[15],对初始的多芯片LED阵列进行二维优化,并在此基础上利用果蝇优化算法对阵列中芯片的位置进行三维空间的优化,使LED阵列照度均匀度进一步提高。三维空间的优化过程将采用MATLAB软件编程仿真模拟,得到的最佳结果将采用TracePro光学软件进行验证,从而得到照度均匀度最优的芯片阵列位置参数。
2 实验模型
2.1 光学模型
如图1所示,LED按要求分布在以面板E(其z坐标为0)为底面的一个三维空间内,并将接收面板F均匀地分为10 000份。在此先对LED芯片作出如下假设:LED芯片所发射出的光满足朗伯特分布,并且无损耗,其光强可以由如下余弦公式表示:
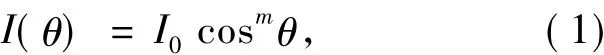
其中,θ为光线与光轴夹角,I0为轴线上的光强[16-17],m 为光源辐射模式,与半功率角 θ1/2处光照强度有关[18-19]:

位于三维空间内点A(X,Y,Z)上放置的 LED芯片在接收平面上点B(x,y,z)处产生的光强照度为[20-21]:
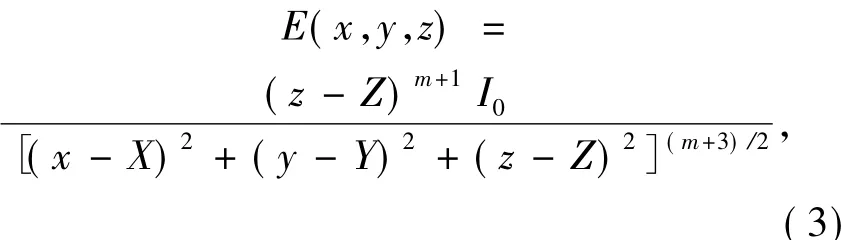
在三维空间内分布的LED芯片阵列在接收平面上点B(x,y,z)处产生的总光照强度为:
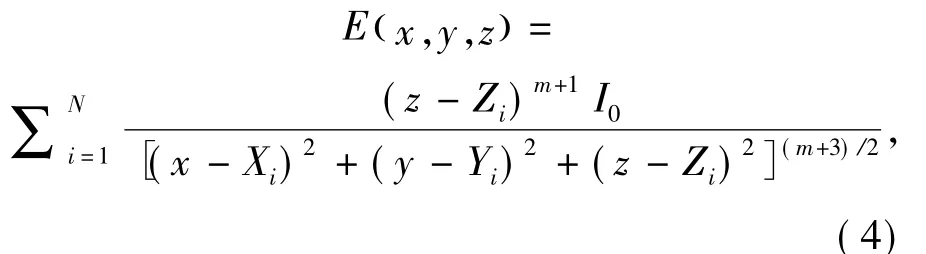
接收平面F可近似视为被均匀地分为N份,其中N=1 000,接收平面F上光照强度的平均值为E:
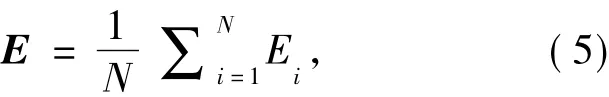
三维LED阵列的光照效果可以以接收平面F上的照度均匀度为衡量标准,利用标准差公式(6),通过MATLAB软件计算出各组实验的标准差σ。σ值越小,说明离散程度越小,接受平面上照度均匀度越高[19]:


图1 LED光照模型Fig.1 LED lighting model
2.2 算法模型
如图2、3所示,本实验设计了一种改进的果蝇优化算法,可以用于多芯片三维LED阵列的迭代寻优,改进的果蝇优化算法主要步骤及原理[22]如下:
(a)选取多个果蝇群落,设置它们的种群大小与迭代数目等参数,并赋予果蝇群落随机的初始位置、位移方向与位移大小。
(b)计算果蝇离原点的距离的值,该值的倒数即味道浓度判定值,即

(c)令式(6)LED阵列照度均匀度的标准差公式为果蝇优化算法的味道浓度判定函数。将各果蝇群体的味道浓度判定值(S1,S2,S3,……)代入味道浓度判定函数,得到所有果蝇群体的气味浓度,从而得到使味道浓最小的各果蝇群体位置分布。
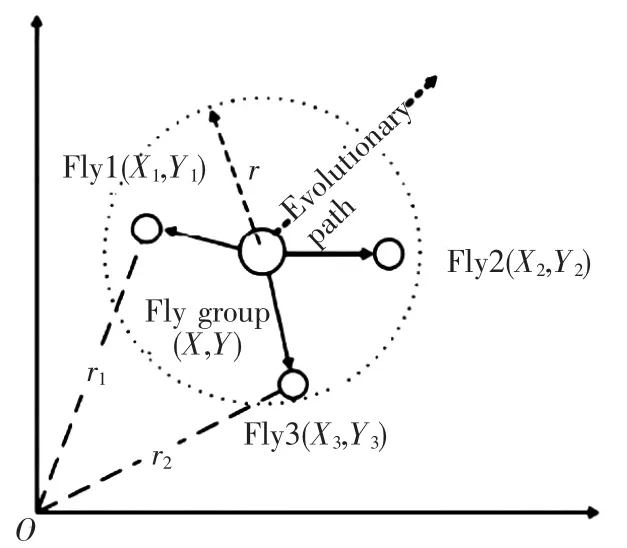
图2 果蝇优化算法图解Fig.2 Diagram of fruit fly optimization algorithm
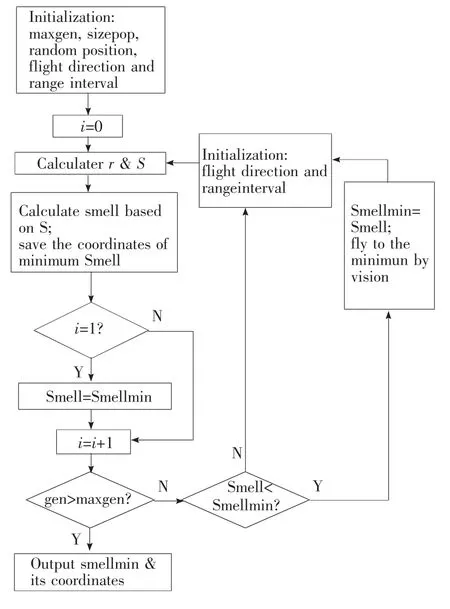
图3 果蝇优化算法程序结构Fig.3 Flow chart of the procedure structure of fruit fly optimization algorithm
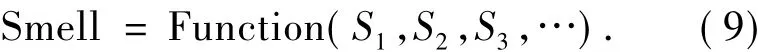
(d)各果蝇群体按照该位置分布排列向新的位置飞去。
(e)多次迭代,重复(b)(c)过程,判断新一轮迭代所得的综合味道浓度是否更小,若是,则重复(d)过程。
3 实验设计及结果分析
本实验所选用的LED芯片尺寸为1 mm×1 mm×0.1 mm,每个芯片的轴线方向光照强度为2 800 mcd,发光面出射光线数为1 000条。在离原点距离z=100 mm处放置一个接收面板F,面板F被均匀分为了10 000份,面朝LED阵列的一面设为对光线完全吸收。本实验设计了如图4排布的两个初始LED阵列,在二维优化的基础上再进一步对其进行三维空间内的优化。

图4 LED阵列二维排布方式。(a)圆形LED阵列;(b)方形LED阵列。Fig.4 Two-dimensional arrangements of chips.(a)Circular LED array.(b)Square LED array.
3.1 圆形LED阵列设计及分析设置一个包含8个LED芯片的圆形二维
LED芯片阵列,取半径为R,其排布如图4(a)所示。令
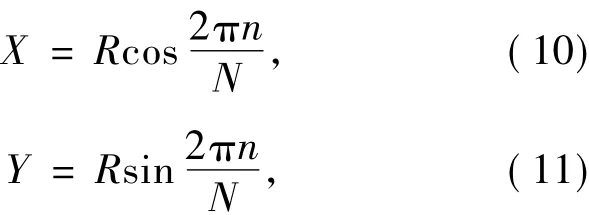
代入式(4),并令Z=0,则可以得到二维圆形LED阵列的光照强度表达式
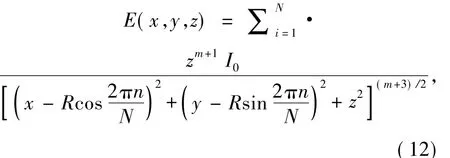
其中,N=8,为阵列所用LED芯片数;n指第n颗LED芯片。取圆形LED阵列的初始半径为120 mm,目标平面大小为300 mm×300 mm,测得初始圆形LED阵列在接收平面上的照度分布效果如图6所示,照度均匀度为49.7%。
参考Ivan Moreno提出的圆形LED阵列二维平面优化方法[12],根据斯派罗法则,在 x=0,y=0时,令(2E)/(x2)=0,可以得到照度的最大平坦条件

即圆形LED阵列二维优化半径取值应不大于81 mm,则本实验取圆形LED阵列半径值为16 mm,并配合半径选取接收平面大小为80 mm×80 mm。
接着采用MATLAB软件进行圆形LED阵列的三维优化。对于三维圆形LED阵列,其光照强度表达式为式(4)。令式(6)为味道浓度判定函数,迭代求得最小的味道浓度。此时优化后的LED芯片位置组合如表1所示。图5所示为味道浓度判定函数的收敛情况,可以看到圆形阵列对应的味道浓度判定函数逐渐收敛于2.509E-4。

图5 圆形三维LED阵列迭代寻优过程Fig.5 Optimization process of 3D circular LED array

表1 圆形三维LED阵列优化坐标参数Tab.1 Optimized coordinates of 3D circular LED array
经二维优化的圆形LED阵列与经三维优化的圆形LED阵列在接收平面上的照度分布效果如图 7、8所示,照度均匀度分别为 70.7%、96.0%。相较于初始圆形LED阵列49.7%的照度均匀度,经二维优化后,圆形LED阵列照度均匀度提升了21%;二维优化的圆形LED阵列再经三维优化,照度均匀度又再提升了25.3%。

图6 未经优化的圆形LED阵列照度分布效果图Fig.6 Illumination distribution of the original circular LED array

图7 二维优化后圆形LED阵列照度分布效果图Fig.7 Illumination distribution of the optimized 2D circular LED array

图8 三维优化后的圆形LED阵列照度分布效果图Fig.8 Illumination distribution of the optimized 3D circular LED array
3.2 正方形LED阵列
如图4(b)设置一个包含9个芯片的正方形LED阵列,芯片呈3×3排布,相邻的芯片间距d恒相等,中心的LED芯片位于坐标系原点位置。该正方形LED芯片阵列的光照强度表达式为
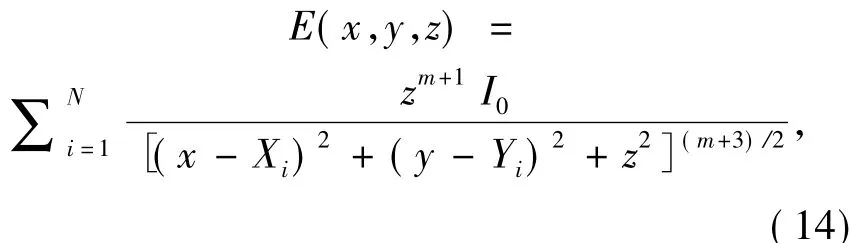
其中,N=9。令正方形LED阵列的初始间距为120 mm,取接收平面为360 mm×360 mm,初始正方形LED阵列在接收平面上的照度分布效果如图10所示,测得照度均匀度为83.0%。
参考Ivan Moreno同时提出的正方形LED阵列二维平面的优化方法[12],根据斯派罗法则,在x=0,y=0 时,令(2E)/(x2)=0,可以得到照度的最大平坦条件
即正方形LED阵列间隔的二维优化取值应不大于115 mm,则本实验取方形阵列的芯片间距为30 mm,并选取接收平面大小为50 mm×50mm。
对于正方形三维LED阵列,其光照强度表达式同样为式(4)。设定式(6)为味道浓度判定函数,经算法寻优后,正方形三维LED阵列坐标参数如表2所示。如图9所示,味道浓度判定函数收敛于2.42E -4。
使用TracePro对未经优化的方形LED阵列以及优化后的方形LED阵列进行仿真,仿真得到的照度分布效果图如图11、12所示。对比图10、11、12的照度均匀度,未经优化的正方形LED阵列照度均匀度为83.0%,经二维优化后照度均匀度提高了6.7%,为89.7%;二维优化的正方形LED阵列再经三维优化后提升了7.7%,为97.4%。

图9 正方形三维LED阵列迭代寻优过程Fig.9 Optimization process of 3D square LED array

表2 方形三维LED阵列优化坐标参数Tab.2 Optimized coordinates of 3D square LED array
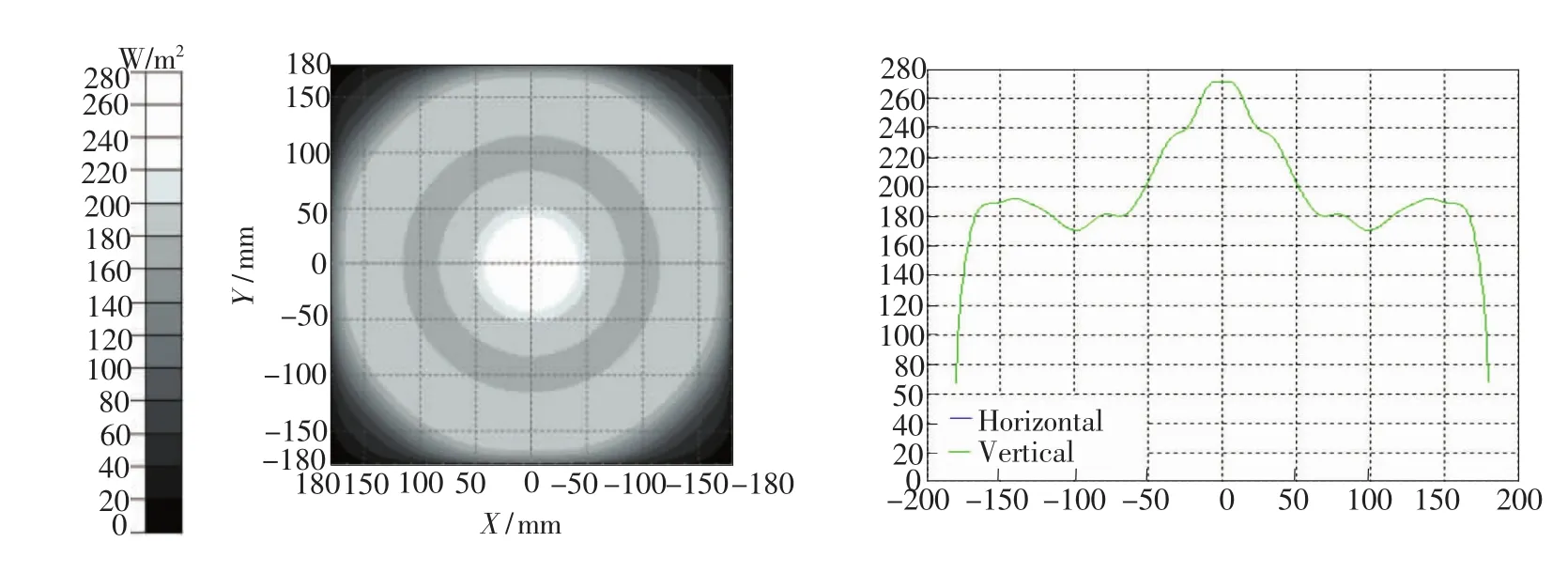
图10 未经优化的正方形LED阵列照度分布效果图Fig.10 Illumination distribution of the original square LED array

图11 二维优化后正方形LED阵列照度分布效果图Fig.11 Illumination distribution of the optimized 2D square LED array

图12 三维优化后的正方形LED阵列照度分布效果图Fig.12 Illumination distribution of the optimized 3D square LED array
4 结 论
本文根据Ivan Moreno提出的方法对初始圆形LED阵列与正方形LED阵列进行二维优化,采用MATLAB软件,结合果蝇优化算法,对两个二维平面阵列进一步进行三维空间上的优化,得到照度均匀度最优的LED芯片空间位置参数。使用TracePro对MATLAB的仿真结果进行验证,得到两种阵列的照度图与照度均匀度:三维优化后的圆形LED阵列的照度均匀度为96.0%,相较于二维优化后的圆形LED阵列提高了25.3%;方形阵列的照度均匀度为97.4%,相较于二维优化后的圆形LED阵列提高了7.7%。综上,根据Ivan Moreno所提出的方法对初始LED阵列进行二维优化,再通过果蝇优化算法对其进一步进行三维曲面优化,使用MATLAB软件仿真,可以快速、有效地得到具有高照度均匀度的LED光源阵列,这不仅为LED阵列的优化设计提供了新的思路与理论依据,还实现了三维LED阵列的计算机智能优化设计,节约了大量的生产成本。
