基于Kinect的全向移动平台视觉伺服控制研究
2018-08-28,,
,,
(1.哈尔滨工业大学机电工程学院,黑龙江 哈尔滨 150001;2.苏州大学机电工程学院,江苏 苏州 215006)
0 引言
全向移动平台由于其完整约束的运动特性被广泛应用于工业生产及特殊作业中[1]。近年将传统机器人技术同其他类别的学科或理论进行融合和研究已经成为一种新兴趋势。如基于ROS并融合物联网技术设计的全向移动机器人系统,用于解决工业上的实际问题[2]。特别对于人机交互方向,由于微软研发的Kinect相机自身可方便同用户交互及能够依据具体需求进行算法开发等优势,越来越多的国内外研究人员将Kinect相机应用于机器人对目标信息的获取及动作模仿、行为跟踪等新型的交互控制中[3-5]。
文献[6]利用多个Kinect相机开发集成的无标记步态跟踪系统,提出基于几何原理的人体步态数据优化测量方法;文献[7]通过对具体身体部位的分析和人体活动情况进行约束的策略,改进基于骨骼跟踪的人体活动识别系统,提高识别的准确率;文献[8]提出利用Kinect对中风患者的行走运动情况进行监测,用于评估病情情况,并总结两者的相关性程度,可应用临床及家用。
设计出平台的构型并分析其运动学模型,考虑利用Kinect相机的交互特点获得目标的特征信息,并将其用于平台的视觉伺服控制中可实现人体跟踪,相对于传统双目立体视觉伺服控制可减少视觉测量的运算量,同时避免运动过程中深度测量值受外界光照等因素影响而失真。给出伺服控制中雅可比矩阵深度值估计方法,通过讨论彩色图像及深度图像设置的增益值组合对平台运动的影响,以仿真形式验证所提方法及控制系统的可行性。
1 平台的运动学模型构建
1.1 全方向移动平台的构型设计
设计的移动平台底盘的3维结构图如图1a所示,全向轮选择omni轮,并以四轮正交分布的方式进行配置,实现移动平台整体的前后行进、左右移动及原地转动3个自由度。对于Kinect相机与平台的连接方式采用“eye in hand”方式,整体形式如图1b所示。
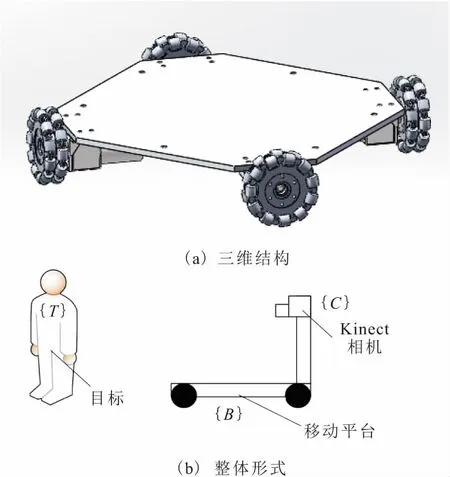
图1 移动平台的构型设计
1.2 平台运动学模型的构建
为方便分析讨论,建立图2所示坐标系,其中B为平台的几何中心,移动平台的理想化坐标系为∑BXBYBZB,坐标系∑WXYZ为已知的参考坐标系,∠θ为两X轴夹角,逆时针为正,∑BXBYBZB在参考系中的位姿可写成A=[x,y,θ]T,则平台坐标系相对于参考系的旋转变换矩阵为:
(1)

图2 平台坐标系与参考系

(2)
已知四轮转速,反向推导转角θ及V=(vX,vY,ωZ)T,得到下式:
(3)
(4)

2 基于图像的视觉伺服控制模型

(5)
对上述偏差设置比例增益,分别设为k1,k2,且为正数,令其产生的像素偏差速度为:
(6)
由文献[9]对于得到上述特征点的像素变化速度与平台运动速度的关系:
(7)
故由式(5)~(7)得到移动平台在参考系∑WXYZ中的3个自由度的速度:
(8)
通过对以上过程的迭代运算,直至特征点的实际像素坐标同期望像素坐标重合,而实际的像素坐标不可能达到亚像素级,故设定由特征点在运动时的像素偏差值小于一个像素,即认为已到达期望的图像像素坐标。
3 基于图像的视觉伺服控制系统设计
以移动平台为控制对象,对其进行基于图像的视觉伺服控制,设计如图3所示的控制系统方案,首先,由Kinect对场景中的图像进行采集,目标通过移动平台上方的Kinect摄像头完成图像采集,进行特征点的提取,移动平台依据当前特征点与给定特征点的偏差进行位姿调整,并通过图像的雅可比矩阵将调整信号转换成速度控制信号;最终作用于平台本体,在此过程中,通过视觉反馈继续获得输出位姿,并不断调整至期望值。

图3 基于图像的视觉伺服控制系统
3.1 特征点的选取与提取
视觉伺服控制中能代替目标的特征点信息对伺服控制的实现是至关重要的,即在摄像头中特征点的像素信息及在摄像头坐标系中的方向的深度信息,对特征点检测效果的好坏将直接影响对移动平台的运动控制,对于目标本身而言,其自身的运动及姿态变化也同样会影响整个控制过程。同时,对于伺服控制本身,也需要实时的深度信息获取,由式(8)可知,若输入变量为特征点在像素平面内的运动速度,输出量为平台的移动速度,故需至少两组特征点的信息;而对于单一特征点,Kinect可在深度相机及彩色相机获取其对应像素值及深度信息,故可将两组特征信息用于雅可比矩阵的求逆运算,从而控制平台运动。
而人体在环境中产生位姿变化会导致上述关节点在空间中的位置变化,同时会带来部分关节点在检测时丢失或关节点在图像空间中的位置重合,从而影响特征信息的获取,而由于四肢灵活度较高,在人体位置确定时,其会产生各类姿态,故考虑以位于人体中央位置的脊柱中央关节点作为特征点,并调用Kinect深度相机的人体骨骼获取函数来获得其特征信息,将其在彩色相机及深度相机中的像素坐标及深度值作为控制信息的输入。
3.2 雅可比矩阵中深度值的估计方法
由式(8)可知,图像的雅可比矩阵中的参数分类可为同相机内参相关的参数(包括深度及彩色相机的等效焦距及主点像素坐标),提取的特征点在摄像头坐标系的深度值,以及特征点在两相机中的对应像素坐标。

ΔM=R(YC1,-ωZ×Δt)×Trans(VX×Δt,0,VY×Δt)
(9)
由于点P在坐标系∑Ixy与∑CXCYCZC的坐标关系可表示为:
(10)
则摄像头在初始位姿下的深度及图像平面的像素坐标已知时,其对应的其余两方向坐标可表示为:
(11)

(12)
4 不同增益值组合对平台运动的影响
设特征点在彩色相机图像平面的初始像素坐标为(568,257),在深度相机图像平面的对应初始像素坐标为(116.797,104.704),彩色相机的期望像素坐标为(1 143,358),深度相机图像平面的对应期望像素坐标为(313.879,137.583),初始深度值为1.59 m,设相机初始点的外参数矩阵为:
彩色相机和深度相机内参数矩阵分别为:
理想的控制结果是能够在保证Kinect相机从特征点的初始像素坐标到达期望像素坐标的前提下,移动平台及摄像头的各自由度的运动速度最大值不超过设定速度,且能实现运动速度的收敛,而同时要考虑收敛至与期望像素坐标的偏差阈值附近的时间,以下分别对两参数进行控制结果的影响分析,由此得出较为理想的参数组合,用于后期实验。分析比例增益K对于平台运动速度的影响,其中采样时间ts取为15 ms,K取值如下,移动平台在笛卡尔空间中的速度变化情况如图4所示。
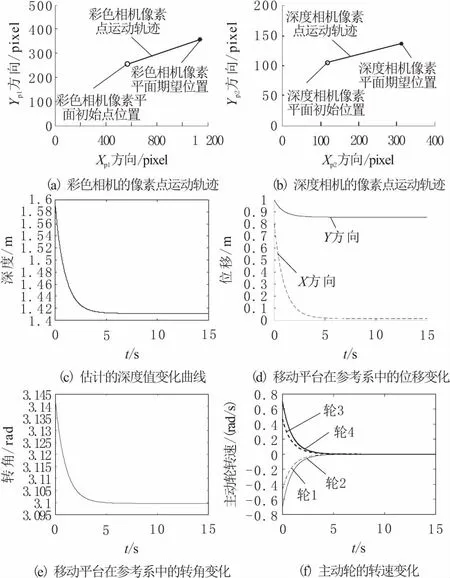
由以上结果可知,当K1=K2时,速度变化曲线更为平稳,随着增益值的增大会导致平台的初始运动速度加快,但同样缩短了收敛至稳态值的时间,其中,在参考系中的X方向的速度增大变化最为明显,而Y方向的速度变化、Z方向的转动速度变化及两者的初始速度值均较小;当K1>K2时,ωZ初始值变大,同时VY出现小范围波动,但VX基本无明显波动,但其会随着增益变大而变大,收敛时间也会变短;当K1 图4 ts=15 ms时不同增益值对移动平台的速度变化仿真结果 考虑平台2个方向的初始移动速度值不宜过大(不超过1 m/s),3个自由度的速度收敛至稳态时间不宜过长(<5 s),故选择增益值组合为K1=1,K2=1,其X方向的移动速度初始值最大为0.830 6 m/s,其收敛最慢,迭代循环至294次时,对应时刻为开始后的4.41 s,结果显示减小至0.01 m/s以内,故可选此组增益值进行平台视觉伺服控制效果的仿真,设平台的初始位姿为(0.8 m,1 m,π),采样时间为ts=15 ms,采样循环为1 000次,利用前述对于移动平台运动学模型的构建,得到参考系下基于图像的视觉伺服控制输出的平台位姿,其控制的仿真迭代结果如图5所示,其中,设Xp1方向为Kinect相机彩色图像平面的水平方向,Yp1方向则为对应竖直方向,Xp2方向为深度图像平面的水平方向,Yp2方向为对应竖直方向。 仿真显示,在平台开始运动的5 s内,特征点在Kinect相机的初始像素坐标均运动至期望的像素坐标,其在图像平面中的运动轨迹为直线,在期望像素坐标附近,移动平台的速度及转速减慢,且伴随着收敛速度的减缓,移动平台在参考系中的位姿由初始时的(0.8,1,π)运动至(-0.033 6,0.848 6,3.099 7),其运动的收敛时间及在彩色及深度相机的像素坐标运动情况满足控制要求。 图5 移动平台的视觉伺服控制仿真 给出了基于Kinect的全向移动平台构型,并推导其正逆运动学模型,建立基于图像的视觉伺服控制的理论模型,设计伺服控制系统,提出控制中特征点的选取及提取的方式。为避免测量值受到干扰,给出雅可比矩阵中深度值的估计方法,讨论不同增益值组合对平台运动的影响,选择符合实际要求的一组增益值,对控制系统进行仿真,仿真结果表示其可行。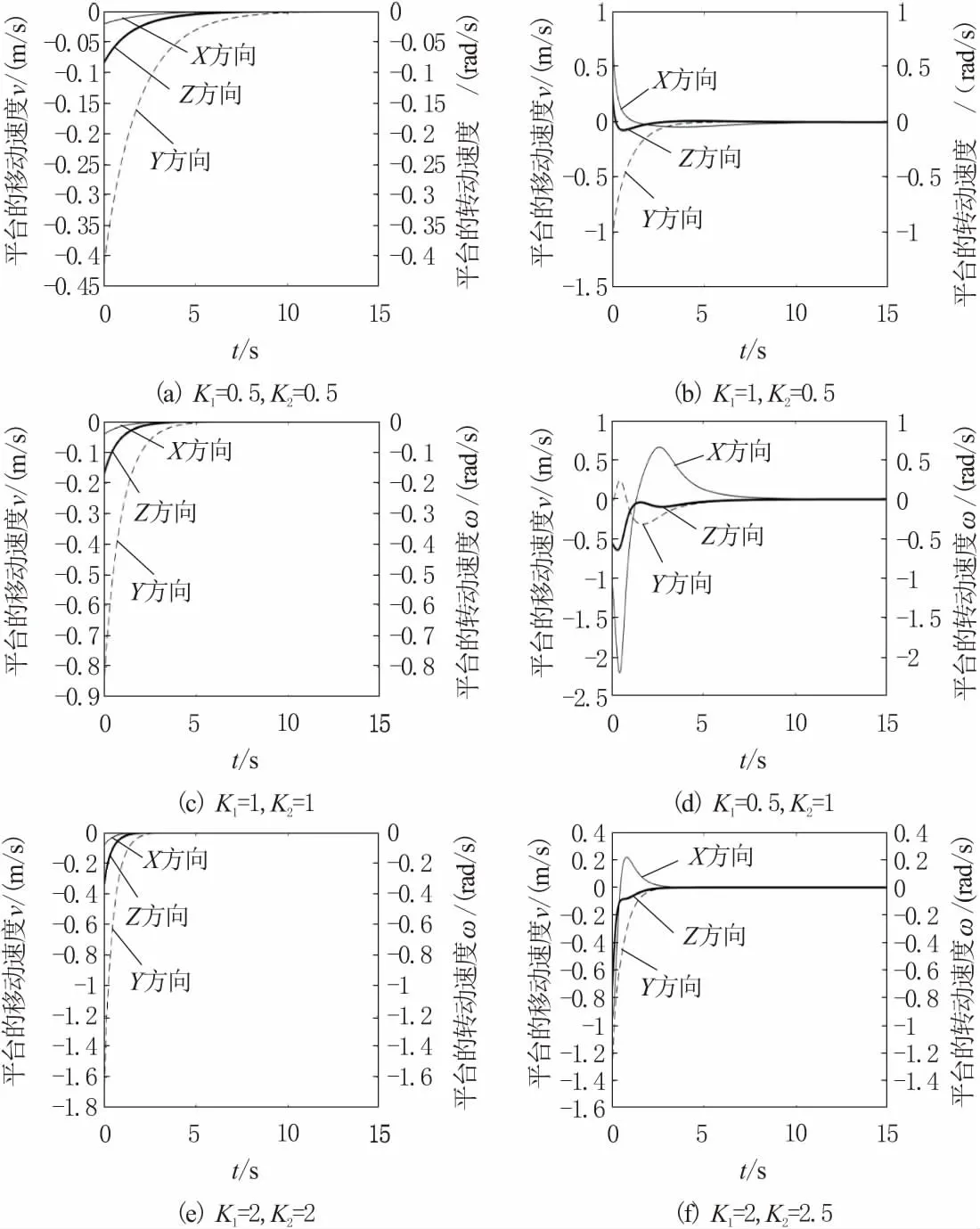
5 伺服控制系统的仿真验证
6 结束语
