直列四缸发动机曲轴扭转振动固有特性分析
2018-08-28张洪飞闫守成
张洪飞,闫守成
1 引言
曲轴扭转固有特性分析是扭振减振器设计的基础,当前较成熟分析方法包括基于有限元模型和基于集总参数模型两种模态分析法。前者为简化处理,将无限个自由度实体模型经单元网格划分简化成有限个自由度有限元模型,是实际结构和物质数学表示方法,有限元分析方法是目前工程分析的主要方法[1]。后者实际形态很复杂,每个轴段都是即有惯量又有弹性振动体,这样数学模型无法处理。依照经典振动理论,按照振动特性不变原则,将一个实际曲轴简化成可进行数学运算理想系统,假设曲轴只有转动惯量无弹性变形的一些集中质量和一些只有弹性而无转动惯量的弹性轴段组成。
对扭转振动研究:文献[2]搭建发动机曲轴平面模型,采用传递矩阵法获得曲轴扭转振动和弯曲振动解;文献[3]搭建曲轴三维空间模型,采用传递矩阵法获得曲轴扭转振动、轴向振动和两个横向振动的解;文献[4]分析基于实模态灵敏度分析结构动力学修改原理用于扭振控制;文献[5]搭建试验台对比安装与否减振效果进行对比,提出减振措施。
以某四缸汽油发动机曲轴轴系为例,分别用基于有限元模型和集总参数模型模态分析法计算曲轴轴系扭转固有特性。同时明确基于有限元及集总参数模型进行曲轴扭转固有特性分析关键点,基于完整曲轴有限元模型,特别是活塞连杆机构的几种等效方法以及集总参数模型中曲轴各段扭转刚度的有限元全模型计算方法。对两种方法获得曲轴的扭转固有频率进行对比。
2 曲轴轴系有限元模型模态分析
2.1 曲轴有限元模型
应用Pro/Engineer中建立某款直列四缸汽油机曲轴模型,导入ANSYS建立有限元模型,进行模态分析和各轴段扭转刚度求解。在建立有限元模型前要对曲轴的三维实体数字模型进行简化,将活塞连杆组以及飞轮总成等结构删除,在模态分析中用Mass点代替[6]。曲轴轴系相关参数,如表1、表2及图1所示。

表1 曲轴轴系的材料参数Tab.1 Material Parameters of Crankshaft System

表2 曲轴轴系的相关参数Tab.2 Parameters of Crankshaft System(质量 m/kg,转动惯量 I/kg·m2,长度 /mm)

图1 简化后的曲轴轴系Fig.1 Simplified Crankshaft System
为便于计算截面扭转角度,预先将曲轴横向切分为若干段,各截面,如图2所示。截面1为曲轴上皮带轮轮毂键槽横向中央截面,截面 2、4、6、8、10 为主轴颈中央截面,截面 3、5、7、9 为连杆轴颈中央截面,截面11为曲轴与飞轮的接触面。

图2 曲轴分段示意图Fig.2 Schematic Diagram of the Crankshaft
采用8节点Solid45单元,对主轴颈和曲柄轴颈用精度为1网格划分;平衡块和曲拐部分用精度为3网格划分,共得到48794个节点,如图3所示。

图3 曲轴轴系有限元模型Fig.3 Finite Element Model of Crankshaft System
将所有节点坐标转换为以曲轴中心线(z轴)为轴线柱坐标,便于后续施加转矩载荷和径向约束。将活塞连杆组、飞轮总成等效为相应集中质量或转动惯量;在图3中A1~A4、B等硬点所生成节点上创建相应等效Mass单元。将各Mass单元与其附近节点形成一刚性区域,确保Mass单元等效集中质量和转动惯量正常参与曲轴动力学行为[7]。
2.2 模态分析
在有限元模型基础上,施加约束,进行轴系扭转振动模态分析。实际运行时受主轴承对曲轴主轴颈支撑作用。轴系扭转固有频率远小于弯曲固有频率,在分析扭转固有特性时可对有限元模型进行简化。由于只分析扭转固有特性,将每个主轴颈径向施加约束,既能略去其他模态,又能得到准确的扭转固有频率[8]。
采用ANSYS中模态分析法,分析1 Hz以上(以滤去刚体转动模态)5阶模态。所分析四缸汽油发动机曲轴系第一、二阶扭转模态频率分别为477 Hz、1214 Hz。其中,第一阶扭转模态节点在飞轮前端的主轴颈上并靠近飞轮,阵型正常。
3 集总参数模型模态分析
3.1 集总参数模型
直列四缸发动机曲轴简化成六自由度当量轴盘系统,当量盘只包含转动惯量不包含刚度,当量轴只提供刚度不包含转动惯量。以各轴颈中央截面为界将轴系划分成若干段,每一段用一个集中转动惯量代替连续体转动惯量[9]。刚度即是每个连续质量之间实际刚度,集总参数模型各质量块转动惯量和各质量块之间刚度转化,如图4所示。以图4(a)所示各主轴颈中央截面为界将轴系划分成六段,各段转动惯量对应图 4(b)所示 I1~I6。图 4(b)所示各自由度之间扭转刚度 K1~K5分别为图 3 中截面 1~3、3~5、5~7、7~9、9~11 之间曲轴轴段的扭转刚度。

图4 多自由度集总参数模型的简化Fig.4 Simplification of the Lumped Parameter Model
曲轴六自由度简化模型,自由振动矩阵方程:


求解式(1)关键在于集总参数模型中转动惯量与扭转刚度计算。
3.2 转动惯量计算

式中:d m—微质量;r—微质量到回转半径距离;m—物体的总质量。
基于有限元模型求得各零件转动惯量,曲轴各段质量块模型,如图5所示。
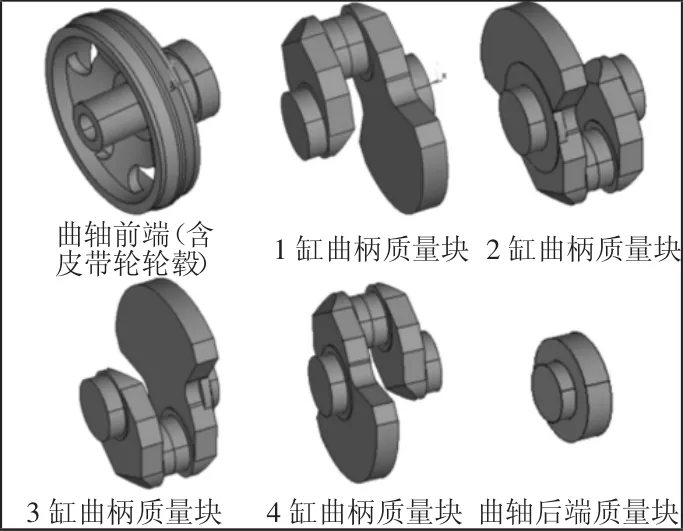
图5 各质量块模型Fig.5 Each Mass Block Model
计算得到曲轴各轴段转动惯量,如表3所示。

表3 曲轴轴系的当量转动惯量Tab.3 Equivalent Moment of Inertia of Crankshaft(转动惯量 I/10-3kg·m2)
3.3 扭转刚度计算
轴段扭转刚度:扭转轴段使其旋转单位角度(1rad)时所需要的扭矩[10],则:

式中:M—扭矩;Δφ—轴两端相对扭转角度;G—轴段材料剪切弹性模量;Jp—截面极惯性矩;L—轴段长度。
曲轴各轴段扭转刚度是一个很难确定参数,可采用经验公式进行推算,如西马年科公式、卡特公式,如式(4)、式(5)所示。

采用直接法和间接法两种方法计算曲轴各轴段扭转刚度。如图2曲轴分段,直接法为计算曲柄轴颈中央截面3、5、7、9及1、11 截面转角,直接得到 1~3、3~5、5~7、7~9、9~11 轴段两端截面相对转角,进而得到相应轴段扭转刚度;间接法为计算主轴颈中央截面 2、4、6、8、10 及 1、11 截面转角,分别求得 1~2、2~4、4~6、6~8、8~10、10~11轴段两端截面相对转角,进而得到相应轴段扭转刚度,由于平衡块对扭转刚度影响可忽略,且 2~4、4~6、6~8、8~10轴段分别关于3、5、7、9截面对称,按照刚度串联法求得2~3、3~4、4~5、5~6、6~7、7~8、8~9、9~10 轴段扭转刚度,再将相关轴段串联得到 1~3、3~5、5~7、7~9、9~11 轴段扭转刚度。直接法扭转刚度求解,如表4所示。间接法求解,如表5所示。

表4 直接法计算曲轴轴段扭转刚度Tab.4 Calculation of Torsional Stiffness of Crankshaft by Direct Method(转角θ/e-4rad,力矩 M/N·m,刚度K/105N·m·rad-1)

表5 间接法计算曲轴轴段扭转刚度Tab.5 Calculation of Torsional Stiffness of Crankshaft by Indirect Method(转角θ/e-4rad,力矩 M/N·m,刚度K/105N·m·rad-1)
两种方法扭转刚度对比,如表6所示。各轴段扭转刚度相对误差均在6%以内,具有很好吻合性。

表6 直接法与间接法扭转刚度计算结果对比Tab.6 Comparison of Direct and Indirect Methods(刚度 K/105N·m·rad-1)
3.4 集总参数模型求解
设式(1)特解形式为:

则求解式(1)转换成求矩阵I-1K-λE的特征向量与特征值问题。
通过计算得到集总参数模型转动惯量参数和各轴段扭转刚度参数,用MATLAB进行矩阵I-1K-λE特征值与特征向量运算,即得集总参数模型中各阶次扭转模态频率和相应阶次阵型结果。基于直接法与间接法刚度计算集总参数模型前二阶扭转模态频率,如表7所示。

表7 基于两种算法集总参数模型模态频率Tab.7 Modal Frequency
由表7可知,基于直接法与间接法刚度计算集总参数模型前二阶扭转模态频率相差很小,均在3%以内,特别是两种方法扭转一阶模态频率误差仅为0.621%,证明两种刚度计算方法吻合性。
由于直接法刚度集总参数模型无任何假设条件,取该方法结果为最终集总参数模型模态分析结果,集总参数模型各质量块相对振幅,如表8所示。阵型,如图6所示。

表8 集总参数模型各质量块相对振幅Tab.8 Relative Amplitude of Each Mass

图6 集总参数模型振型图Fig.6 Vibration Pattern
4 曲轴扭转固有特性对比
分别采用有限元模型与集总参数模型模态分析方法结果对比,如表9所示。
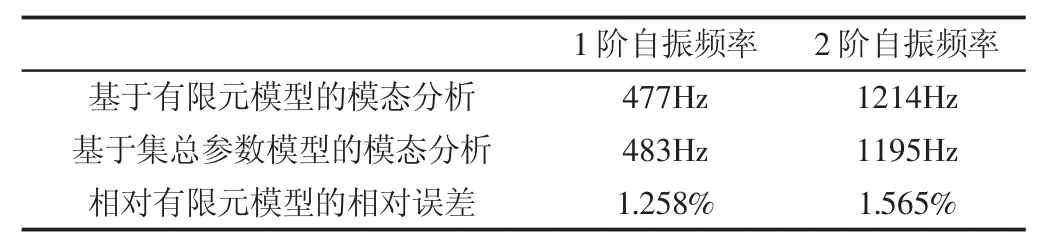
表9 扭转固有特性分析方法结果对比Tab.9 Comparison of Analytical Results
由表9可知,两种分析方法结果相对误差仅在2%以内,基于集总参数模型与有限元模型的扭转固有特性分析结果完全一致,两种分析方法是统一的。
5 结论
对某四缸汽油发动机曲轴同时建立有限元模型和集总参数模型,分别计算曲轴扭转固有频率,对集总参数模型中曲轴各段扭转刚度计算方法进行分析。结果表明:
(1)基于连杆轴颈中央截面分段直接刚度计算法和基于连杆轴颈和主轴颈中央截面分段然后串联间接法两种途径计算曲轴各段扭转刚度一致性好,精度满足工程要求;前二阶扭转模态频率相差很小,均在3%以内。
(2)基于集总参数模型与有限元模型的扭转固有特性分析结果完全一致,两种分析方法结果相对误差仅在2%以内,两种方法是统一的。
(3)两种分析方法及结果一致性,为同类设计研究及扭转减振研究提供可靠固有特性分析方法。
