索网结构找形分析研究
2018-08-28谭也平
谭也平,王 健,张 谦
(深圳大学土木工程学院,广东 深圳 518060)
1 引言
索在房屋建筑结构中应用的历史只有六十几年[1-5], 对于索网结构的找形问题,已经有了广泛的研究。Schek最先提出了力密度法,用于索网结构的找形[6]。Linkwitz和Grundig运用数值分析的方法不断发展和完善了该原理[7-8]。
索网结构作为二十世纪七十年代初德国盛行的空间张拉体系,因其结构效率极高而成为最有发展前景的建筑结构之一。索网结构其结构的空间力学特性,使得索单元在施加预应力之后才能形成稳定的结构。在无使用荷载状态下,结构通过各个索单元的预应力相互作用而处于稳定的平衡状态。基于结构的拓扑关系、预设的力密度值对每一个节点建立静力平衡方程,通过求解平衡方程得到索单元节点坐标。力密度法通过预设的力密度值使求解复杂的几何非线性问题转化成求解一组简单的线性方程组,从而避免了坐标初始值问题以及其他方法致命的收敛性问题,是求解索网结构找形问题的有效方法[9]。
Matlab是由Math works公司开发的一套功能强大的数学软件,也是当今科工程应用最广泛的计算机语言之一。高度集成的数值计算、符号运算、计算机可视化为找形分析提供了便利[10]。完善的科学计算工具和采用矩阵运算的机制使得Matlab编写的找形程序比用C++、FORTRAN等传统语言更为便捷,运用稀疏存储结构存储非零元素可以有效减少矩阵存储量,优化计算过程,从而可以迅速计算出节点坐标,并通过内置的数据可视化功能输出索网结构找形图。
2 力密度法的计算原理
对于索网结构在本文中符合以下假定:
(1) 节点拓扑结构是已知的;
(2)各索单元的节点连接均为铰接;
(3) 在找形过程中不施加外荷载并且忽略结构自重。
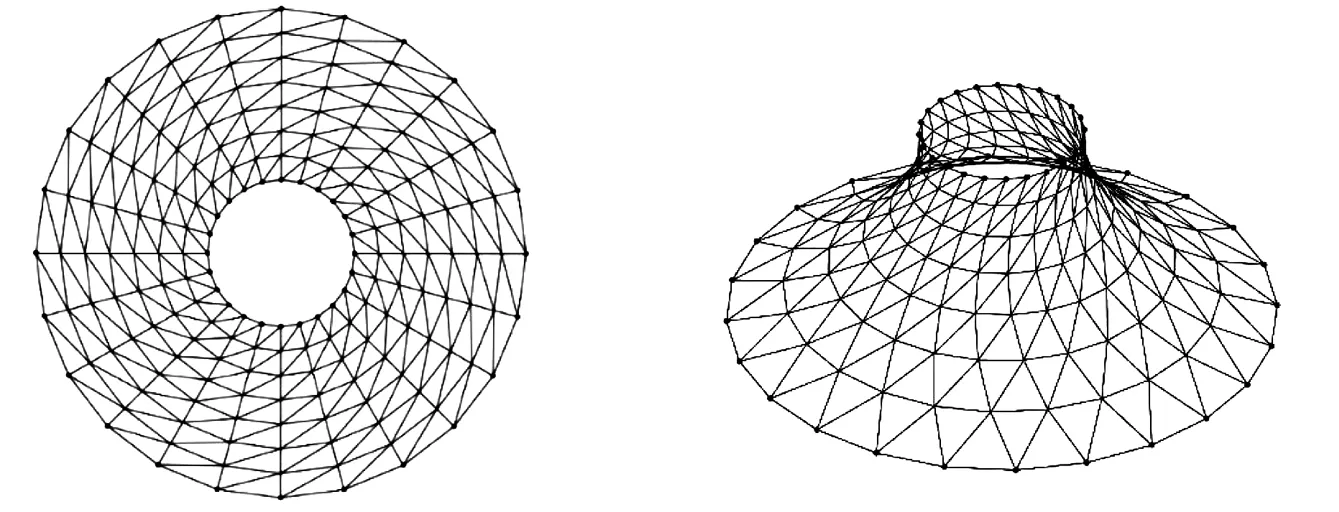
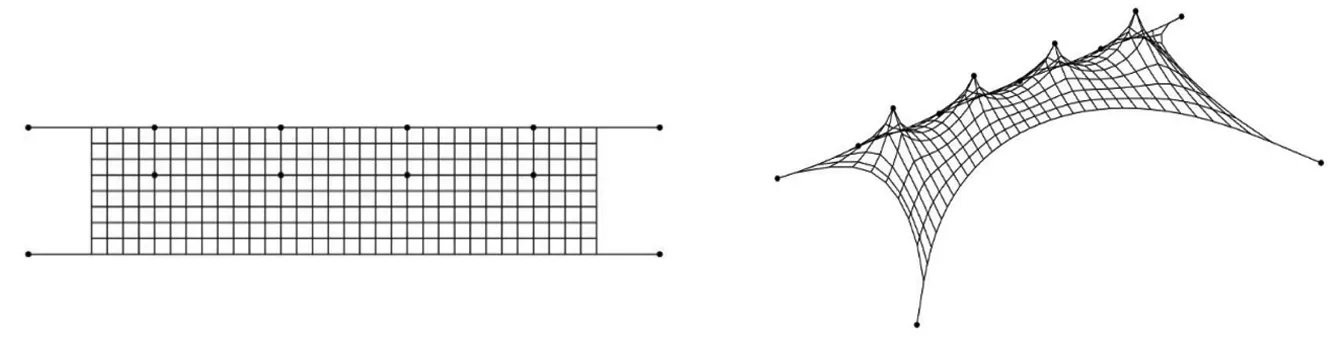
假设有一个具有m个杆单元,n个节点的索网结构。 第k个索单元的节点i和j(i (1) 其中,索单元k的长度 (2) 假设Q是力密度矢量q的对角矩阵: Q=diag(q) (3) 如果索单元k连接到节点和,那么拓扑矩阵Cs=[CCf](C和Cf分别为自由节点和固定节点的拓扑矩阵)的第k行的数值分别设为1和-1,除此之外第k行元素等于0。则拓扑矩阵Cs为: (4) 由拓扑矩阵中各节点的位置关系,可以得出索单元相邻节点的坐标差为: u=Cx+Cfxf v=Cy+Cfyf (5) w=Cz+Cfzf 其中x、y、z为m维列向量节点坐标; 其中xf、yf、zf为固定节点坐标。 根据力密度的定义,由(1)式可以得到索单元的平衡方程为: CtUq=px CtVq=py (6) CtWq=pz 其中U、V、W为u、v、w的对角矩阵;px、py、pz为节点三个方向上的外力;Ct为自由节点拓扑矩阵的转置矩阵。 由矩阵的运算性质有: Uq=Qu Vq=Qv (7) Wq=Qw 联立(5)(6)(7)可得: CtQCx+CtQCfxf=px CtQCy+CtQCfyf=py (8) CtQCz+CtQCfzf=pz 由于找形过程中,索网结构节点无外荷载,节点的平衡方程可以表示为: CtQCx+CtQCfxf=0 CtQCy+CtQCfyf=0 (9) CtQCz+CtQCfzf=0 令系数矩阵D=CtQC,常数矩阵Df=CtQCf,则三个方向的节点坐标为: x=-D-1Dfxf y=-D-1Dfyf (10) z=-D-1Dfzf 由此,只需根据结构拓扑矩阵和预设的力密度值即可得到找形后的节点坐标。 索网结构的力密度找形仿真过程就是根据拓扑矩阵(包括固定节点坐标)和预设的力密度值求解式(10),得到每一个索单元的节点坐标。本文提出了基于稀疏存储结构(sparse函数)的力密度法的格式,根据力密度法计算原理编制了索网结构找形的计算程序,计算流程如图1所示: 图1 找形流程图 算例1对称双曲抛物面是典型的索网结构,结构投影图如图2所示,结构平面为正方形,相邻对角线固定点高差为。总节点数ns=61,mf=4,自由节点数n=57。假设固定节点坐标(黑点表示固定节点)分别为:nf1(-5,-5,0,),nf2(5,-5,4),nf2(5,5,0),nf4(-5,5,4)。索单元数m=120.预设的边界索单元力密度q=100,内部索单元力力密度值q=10,输入结构拓扑信息,根据式(10)编制的程序得到结构的找形结果如图3所示。 图2 双曲面投影图 图3 双曲面找形图 算例2悬链圆环张拉索网结构如图4所示,圆环半径由内到外分别为15m到50m,总节点数ns=192,固定节点数nf=48,自由节点数n=144,杆单元m=528。圆环内外圈固定节点高差为20m, 预设的内外边界索单元力密度值q=100,内部索单元力力密度值q=20,输入结构拓扑信息,根据式(10)编制的程序得到结构的找形结果如图5所示结构。 图4 悬链圆环投影图 图5 悬链圆环找形图 算例3体育场看台顶棚投影图和固定节点如图6所示,该结构平面为32m×8m矩形。其中,总节点数ns=301,固定节点nf=12,自由节点数n=289,杆单元m=556。预设的上下边界索单元力密度值q=50 、150,左右边界索单元和内部索单元力力密度值q=10,输入结构拓扑信息,根据式(10)编制的程序得到结构的找形结果如图7所示。 图6 帐篷投影图 图7 帐篷找形图 (1)索网结构的内力特点在设计时需要进行结构找形分析,力密度法原理可以使找形中的非线性问题线性化,是确定索网结构形状问题的有效方法。 (2)三个算例表明,基于Matlab的稀疏存储结构可以迅速求解出索网结构的节点坐标,其高度的准确性和便捷性适用于大型索网结构的找形分析。 (3)对于给定约束条件如特定的索长、索力及边界约束条件,需要进一步研究的问题是通过力密度法找形得出的初始形状,对其进行带有约束条件的迭代,使得索长、索力满足设计要求。3 程序编制
4 数值算例

5 结语
