基于随机延误情景的城轨网络末班车时刻表调整模型

徐文恺，赵 鹏，宁丽巧，张 辉

(1.北京交通大学 交通运输学院，北京 100044；2.山东建筑大学 交通工程学院，山东 济南 250101)

城市轨道交通网络末班车时刻表调整是指网络中某线路末班车发生延误时，通过调整末班车在换乘站的到发时刻，协调不同线路末班车在换乘站的衔接关系，实现一定目标下的系统最优。末班车间的衔接关系决定着城市轨道交通网络在运营结束阶段的换乘可达性[1]，在末班车运行延误的条件下，网络换乘可达性的变化会导致换乘乘客错失计划换乘，从而无法经由城市轨道交通网络完成出行。因此，当末班车运行发生延误时，有必要结合乘客需求和运营管理要求，及时调整网络末班车时刻表，尽可能保证乘客的正常出行。随着乘客对城市轨道交通系统服务水平要求的提高，该问题具有重要的研究价值和现实意义。

目前，国内外学者主要从末班车换乘衔接的角度研究网络末班车时刻表问题，期望得到一个更优的网络末班车计划时刻表，但针对网络末班车时刻表调整问题的研究较少。文献[2]根据网络中各线路和换乘站的重要度系数确定网络的主协调线路和换乘站，以乘客在换乘站的总候车时间最小化为目标，根据重要度从大到小依次求出各线路末班车在各换乘站的到发时刻。文献[3]通过选取主导衔接关系和主协调换乘站，以成功实现换乘的末班车乘客数量最大化为目标构建网络末班车衔接方案优化模型，并将问题转化为最大生成树问题，借鉴Kruskal算法推算出协同优化的网络末班车时刻表。文献[4]结合路径选择模型，以乘客换乘等待时间最小化和换乘失败乘客数量最小化为目标，设计一种遗传算法求解出各线路末班车在始发站的发车时刻。文献[5-6]通过选取网络的关键换乘方向，以乘客换乘等待时间最小化和成功换乘衔接关系数量最大化为目标构建网络末班车协同优化模型。文献[7]设计一种启发式算法优化网络末班车时刻表，案例分析表明该算法明显优于模拟退火算法和遗传算法。文献[8]建立以乘客总体换乘不满意度最小、换乘成功的乘客数量最多和各线路方向末班车结束运营时间最早为目标的确定环境下的末班车时刻表衔接优化模型，设计NSGA-II算法求解。文献[9]从网络末班车时段出发，构建以总乘客换乘等待时间最小化为目标的末班车时段时刻表协同优化模型。

总之，目前绝大多数关于网络末班车问题的研究集中于网络末班车计划时刻表的编制优化，很少涉及网络末班车运营过程中遭遇突发事件延误后的时刻表调整问题。但无论是网络末班车时刻表协调优化问题还是网络末班车时刻表调整问题，换乘乘客都是研究的重点。本文从乘客的角度出发，以实现换乘的乘客数量最大化为目标；从运营的角度出发，以调整时刻表与计划时刻表的偏离程度最小化为目标构建网络末班车时刻表调整模型。通过ε-constraint法[10-11]，将模型转化为单目标混合整数规划模型，并通过不断调整ε取值，求出相应的近似Pareto最优解，即网络末班车的时刻表调整方案。

1 网络末班车时刻表调整模型

在实际运输生产过程中，当发生列车运行延误时，调度管理人员往往采用赶点、跨站停车、扣车、小交路等措施使列车尽快恢复正点运行，而较少考虑对乘客的影响[12-14]。此外，既有研究中的末班车时刻表模型大多是基于预先确定的主协调线路或关键换乘方向。本文所构建的模型结合网络末班车间换乘客流分布，不选择主协调线路或关键换乘方向，从乘客以及全局优化的角度，协调延误条件下各线路末班车间的衔接关系。

1.1 符号和变量

模型的符号和参数定义如下：

模型的决策变量定义如下：

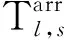
1.2 末班车衔接关系

根据各线路末班车在换乘站的实际到发时刻，每一个衔接关系c存在以下两种情景：

图1 换乘衔接成功

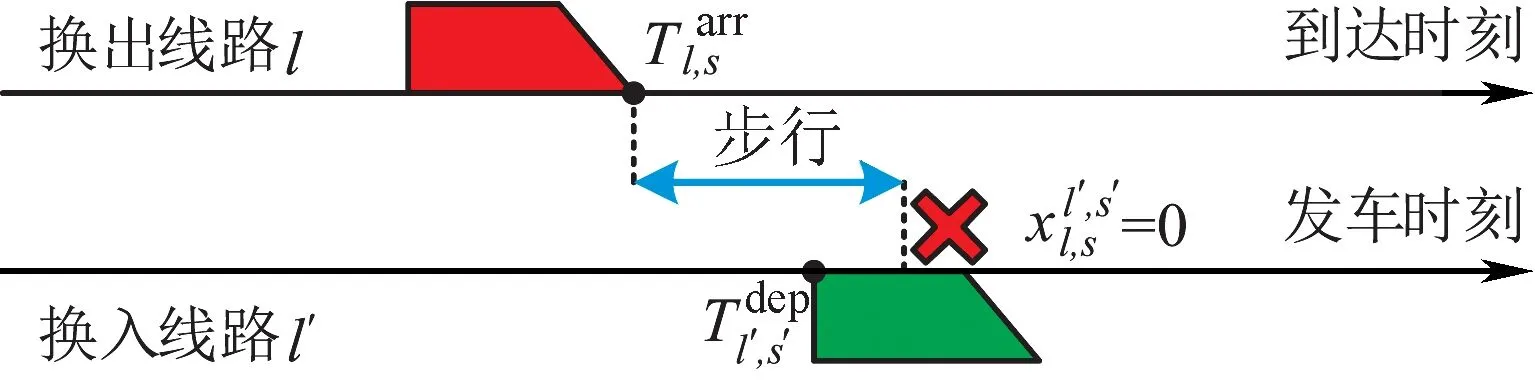
图2 换乘衔接失败

( 1 )

( 2 )

( 3 )

1.3 优化模型

针对网络末班车问题，网络换乘可达性对乘客出行有着十分重要的影响。本模型从乘客和运营两个角度出发，建立目标函数。

( 4 )

( 5 )

式( 4 )从乘客的角度出发，以换乘成功乘客数量最大化为优化目标。从运营的角度出发，当发生列车运行延误时，调度管理人员须尽快使列车运行恢复至计划时刻表，因此，式( 5 )表示调整时刻表与计划时刻表的偏离程度最小化。该目标也有利于降低调整时刻表对非换乘乘客的影响。

模型约束如下：

s.t.

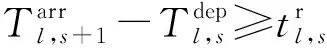
( 6 )

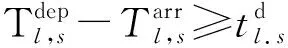
( 7 )

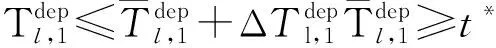
( 8 )

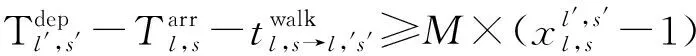
( 9 )

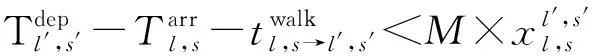
(10)

(11)

(12)

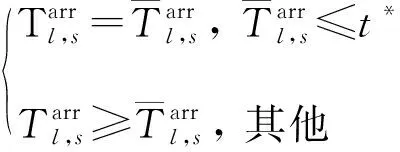
(13)

(14)

式( 6 )、式( 7 )为安全性约束，各线路末班车在区间的运行时间不得小于最短运行时间，在车站的停站时间不得小于最短停站时间[15]。式( 8 )为灵活性约束，对于发生列车延误事件后还未从始发站发出的末班车，允许调整其在始发站的实际发车时刻。式( 9 )、式(10)即式( 2 )、式( 3 )，用于判断各线路末班车在换乘站的衔接关系是否成立。式(11)为初始延误约束，用于输入列车的延误时间及位置。式(12)～式(14)为实际问题决策变量约束。

2 模型求解

本文所构建的双目标优化模型旨在最大化换乘成功乘客数量的同时最小化调整时刻表与计划时刻表的偏离程度，期望得到一组近似Pareto最优解以体现两个目标函数之间的均衡，可以直观地作用于调度管理人员的决策过程。多目标优化模型求解时需要转换为单目标模型，而常用的权重系数法存在权重系数难以确定的问题。因此，本文采用ε-constraint法求解近似Pareto最优解。

选取目标函数式( 5 )作为ε-constraint，将式( 5 )转换为式(15)。

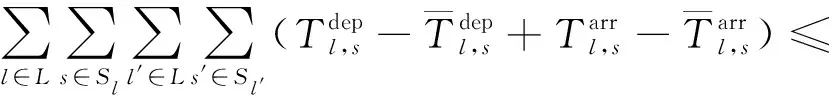
(15)

式中：F*为仅考虑目标函数式( 5 )的条件下模型求得的最优值；ε为调度管理人员对调整时刻表与计划时刻表偏离程度的容忍度，0≤ε≤εmax，εmax为调度管理人员对偏离程度的最大容忍度。

采用ε-constraint法，将本文所构建模型转换为以换乘成功乘客数量最大化为目标的单目标混合整数线性规划模型(MILP)，通过改变ε的取值，使用Cplex软件编程求解出相应的近似Pareto最优解。模型的求解过程如图3所示。

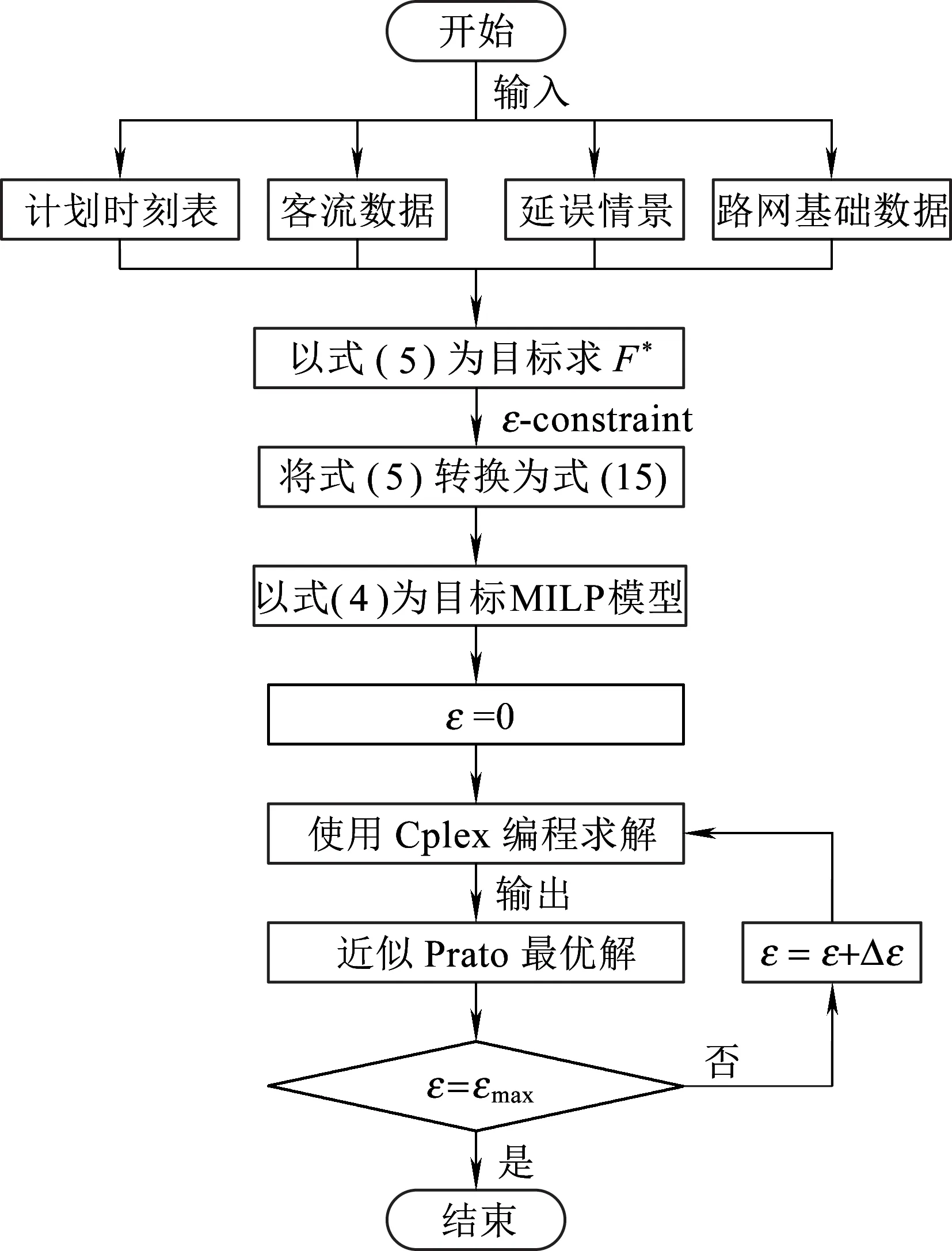
图3 模型求解

3 案例分析

本文以北京地铁网络为研究对象，验证模型的有效性。截至2017年6月底，除机场线外，北京地铁网络共包含18条双线线路，53座换乘站，路网结构如图4所示。由于客流特征等因素的不同，不同的线路有不同的运营时间范围，各线路的末班车计划时刻表详见北京地铁官方网站。

图4 北京地铁路网(不包括机场线)

换乘客流量是决定一个末班车衔接关系是否要满足的关键因素。但清分后的地铁自动售检票(AFC)数据只能给出一段时间内每一个换乘方向的换乘客流量，无法准确得到来自某列车的换乘客流量。因此，在现有的技术条件下我们无法准确获得来自末班车的换乘客流量。本文以各线路最后30 min的AFC数据为基础生成在各个换乘站从末班车下车去往其他线路的换乘客流量。由于本文所提出的模型并不需要提前选取实际路网中的主协调线路或关键换乘方向，所以基于AFC数据生成的换乘客流数据虽然与实际不符，但并不影响验证模型的有效性。

3.1 随机延误情景分析

为验证模型的有效性，本文随机生成若干延误情景，每个延误情景随机选择北京地铁网络中的某条线路，假设该线路的末班车发生延误，延误时间设置为3～10 min。具体延误情景见表1。

表1 延误情景

通过在3.1 GHz CPU, 8 GB RAM台式电脑上使用Cplex软件编程求解每一个末班车延误问题，所有问题均在2 s内求得最优解，可以满足实际运输生产过程中实时性的要求。为验证模型的有效性，设置对比方案，各方案详细求解结果见表2，括号中的百分比代表相对于方案A的提高比例。

方案A：列车运行延误后不进行任何调整，仍然按照计划时刻表中的区间运行时间和停站时间运行。

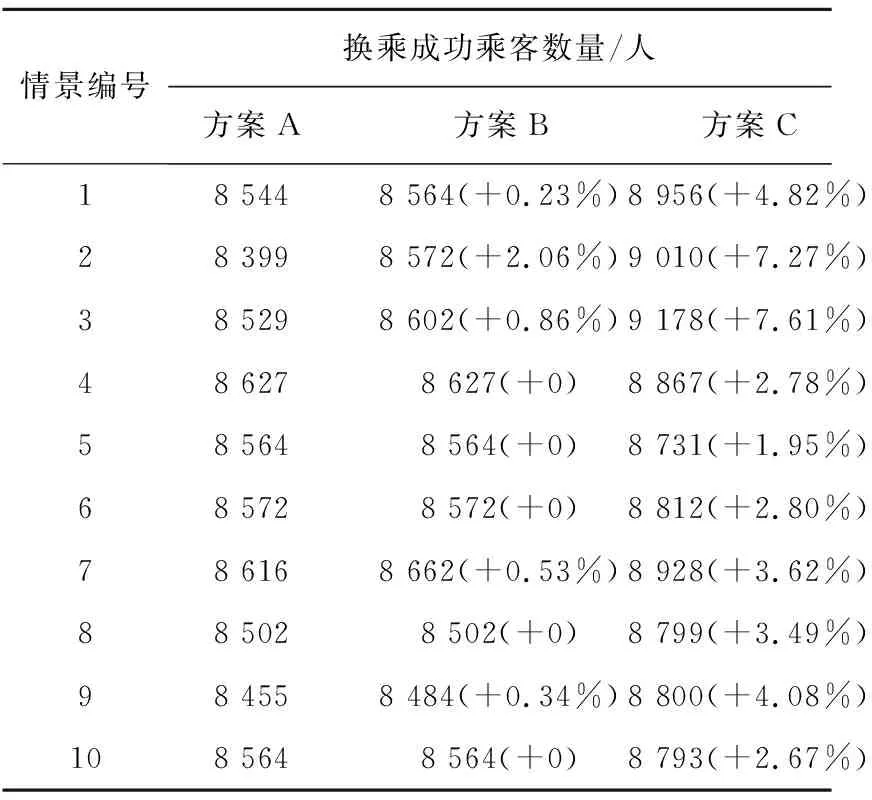
表2 求解结果

求解结果表明，在任意延误情景下，方案B都不比无调整的方案A差，而方案C都要优于方案A。这也说明在末班车延误的条件下，调度管理人员一定要及时响应，科学调整末班车时刻表，保证系统的服务水平。相对于方案B，方案C的优化效果更加明显：在换乘成功乘客数量上，方案C与方案A相比有1.95%～7.61%的增长，而方案B最高也仅有2.06%的提高。方案C可以明显提高末班车延误后系统的服务水平，更好地保证乘坐末班车换乘乘客的正常出行。求解结果证明了本文所提出方法的准确性和有效性。

3.2 近似Pareto最优

Pareto最优是指资源有限的条件下一种理想的资源分配状态，当多目标模型中某个目标函数的函数值变优时必然会导致其他目标函数的函数值变差，此时对应的解即Pareto最优解，Pareto最优解也是资源利用效率最高的解。在给定路网及延误情景的条件下，调度管理人员对调整时刻表与计划时刻表偏离程度的容忍度越高，调整时刻表与计划时刻表的偏离程度越大，相反，各线路末班车在换乘站实现换乘衔接的可能性越大。本文以延误情景1为例，通过改变ε的取值(εmax=0.5，Δε=0.05)，求出相应的近似Pareto最优解，见表3。绘制换乘成功乘客数量与偏离程度散点图，如图5所示。可以发现一个明显的趋势：随着偏离程度的增加，换乘成功乘客数量明显提高。而每一个近似Pareto最优解代表一个时刻表调整方案，调度管理人员在实际运输生产过程中要权衡各方案的优劣，并选择一个最有利的方案。

表3 近似Pareto最优解(情景1)

图5 换乘成功乘客数量与偏离程度散点图

为辅助调度管理人员决策，本文引入参数总运行时间tTotal，是指所有线路末班车从始发站到终点站的运行时间之和。

(16)

根据式(16)计算无调整方案A的总运行时间为99 900 s，计算各近似Pareto最优解的总运行时间见表3。以高偏离容忍度(ε=0.5)求出的时刻表调整方案，换乘成功乘客数量比方案A增加515 (+6.03%)人，而总运行时间仅增加1 227 s。考虑到北京地铁包括18条双线线路、36列末班车，平均每列末班车运行时间仅增加34 s，几乎可以忽略不计。这也说明调整时刻表对非换乘乘客的影响较小。在其他延误情景下，也得到了相似的结果。因此，当网络中发生末班车运行延误时，调度管理人员应该更多的从乘客的角度出发，选择换乘成功乘客数量更多的时刻表调整方案。

4 结论

在网络化运营条件下，换乘衔接质量是衡量城市轨道交通服务水平的重要指标。而针对末班车衔接优化问题，末班车衔接合理与否直接关系到网络换乘可达性的高低。一旦换乘乘客错过其衔接线路的末班车，则意味着该乘客无法通过轨道交通系统完成出行，将严重降低系统的服务水平。

本文针对城市轨道交通网络末班车延误问题，以换乘成功乘客数量最大化和调整时刻表与计划时刻表偏离程度最小化为目标构建了末班车时刻表调整模型，并采用ε-constraint法将模型转换为单目标混合整数线性规划模型，使用Cplex软件可快速求出最优解。在以北京地铁网络为研究对象的案例分析中，随机生成末班车延误情景，使用模型求解出的调整时刻表能够使换乘成功乘客数量增加1.95%～7.61%。在给定延误情景的条件下，改变ε取值，可使用模型求得相应的近似Pareto最优解，为调度管理人员提供决策支持。

案例分析结果表明，随着调整时刻表与计划时刻表偏离程度的增加，换乘成功乘客数量明显增加，而末班车的运行时间没有明显变化：ε=0.5时，换乘成功乘客数量增加了6.03%，而平均每列末班车的运行时间仅增加了34 s，对非换乘乘客影响较小。因此，随着乘客对轨道交通系统服务水平要求的日益提高，当网络中发生末班车延误时，调度管理人员应该在整合分析历史客流数据、末班车延误数据的基础上，合理确定ε取值，选择更有利于乘客的末班车时刻表调整方案。