基于卡尔曼滤波理论的质量数据评估方法研究∗

严锦涛 陈砚桥 刘晓威

（海军工程大学动力工程学院 武汉 430033）

1 引言

由于武器装备应用环境的多样性，使用、维修单位分布的广泛性，数据来源涉及工作项目多，使用装备质量数据主要为日常工作中所记录产生的数据，表面繁杂且无序，使得部队武器装备质量数据具有鲜明的不确定性等特点，从而给装备质量数据管理以及利用装备质量数据进行的质量评估带来了很大难度［1］。加之在装备质量评估过程中，统计数据一般由于系统误差、测量误差等原因，数据波动大且难以找到典型的分布规律，定性因素与定量因素交织，正因如此，采用一种合适的数据评估方法用来评估质量数据是质量评估过程中最为重要且关键的步骤。

卡尔曼滤波理论一出现，就得到了军界的高度重视，在宇航和军备领域里，应用成果层出不穷。有关“阿波罗”登月计划中的导航系统以及C-5A飞机的多模式导航系统等，都是卡尔曼滤波理论提出后早期成功应用的例子［2］。至今，凡是需要进行实时数据处理的场合，卡尔曼滤波一直占据主导地位。在海军舰载指控系统、各种火控系统以及综合导航系统中，应用卡尔曼滤波技术是其现代化水平的重要标志之一［3］。

本文提出基于卡尔曼滤波的质量数据不确定性评估方法，卡尔曼滤波是信号处理和控制理论中的一种标准方法［4～6］。所谓滤波，就是从受到噪声污染的有限观测信号中，提取出被观测系统的参数或状态，不确定性即体现在具有噪声的污染，此处所说的噪声污染其实指的是测量过程中存在的误差，系统则是指装备整体或是某一个部件。卡尔曼滤波是根据与被提取信号有关的观测值去推断或重构出最符合系统状态真值的一个最优估计，因此，卡尔曼滤波本质是一种状态的最优估计，并且是线性、无偏、误差方差最小的一种最优估计，此处所称的滤波与常规滤波具有完全不同的概念和含义，更多的是作为估计方法［3］。其基本思路图如下。

图1 卡尔曼滤波理论思路框图

2 基本理论

对于线性系统数据评估使用基本卡尔曼滤波理论［7］

其中，F、A、C为可能随着时间变化的系统模型矩阵，F为状态转移矩阵，C为观测矩阵，A为干扰转移矩阵，x(k)为状态向量，y(k)为系统观测或输出向量，以及系统随机干扰向量m(k)与已知的协方差矩阵Q(k)和随机观测误差n(k)与已知的协方差矩阵R(k)。为便于表达与计算简单，向量x的估计值用x^表示，同时假定A≡I，为单位矩阵，即把这些误差看成是高斯白噪声，也就是误差跟前后时间是没有关系的而且符合高斯分布。例如，舰上雷达跟踪敌机运动时，雷达的跟踪误差一般可以认为与敌机的运动状态无关，另外，系统的随机干扰与系统初始状态往往也是独立的。

此处考虑状态估计的目标是从系统模型矩阵和观测值 y(k)中对x(k)的序列估计。在序列估计中，状态向量x(k)的估计值及其协方差矩阵P(k)是由k-1时刻x(k-1)的估计值及其协方差矩阵P(k-1)和当前k时刻的系统观测值 y(k)计算得出，当k=0的初始时刻，会给出一个初始的状态向量初始值和初始协方差矩阵。

由文献［7］相应的卡尔曼滤波基本方程为

利用卡尔曼增益矩阵

其中，式（3）为一步最佳预测，式（4）为验前方差阵，式（5）为滤波方程，式（6）为验后方差阵。状态方程式（1）为状态预测提供了基础，由于系统随机干扰m(k)是白噪声序列，而白噪声序列是不相关的，其最佳估计只能是其均值。因此，由状态方程式（1）和已知的x^(k-1)，可得到状态向量的一步最佳预测 xk，k-1。

3 模型的建立

对于线性卡尔曼滤波理论的式（3）～（7），建立测量模型为

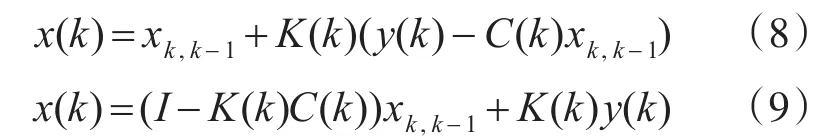
也可以表示为

其中

关于测量模型有以下两种情形：已知的测量模型和未知的测量模型。为便于表达方便与计算简便，本文主要研究基于已知的测量模型的卡尔曼滤波估计。

当系统模型是准确已知的，在式（9）中预测当前状态估计的唯一不确定源是系统观测向量y(k)，误差m(k)和n(k)。与观测向量 y(k)相关的不确定性由协方差矩阵R(k)给出，它代表了观测瞬时k时刻的误差协方差。在最简单的情况下，误差被认为是独立的服从高斯分布的误差（即白噪声），同时已知分布的标准差。对于更复杂的带有误差的结构，可以使用矢量回归（VAR）模型［8］。

假定与估计值x^(k-1)相关的协方差矩阵P(k-1)=Pk-1，k-1可以很有效地代表模型估计中的不确定性，存在多元正态分布：

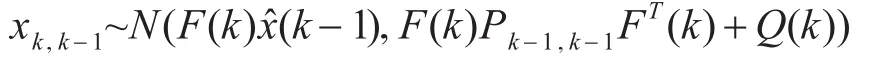
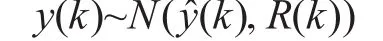
两个输入量都假定是独立获得的，这种情况下它们的联合分布概率密度函数便为其各自概率密度函数的乘积。由于式（9）中的 xk，k-1和 y(k)的测量模型是线性的，且它们服从的分布是正态分布，通过测量模型可以对联合概率密度函数进行计算分析，得出k时刻最佳估计为

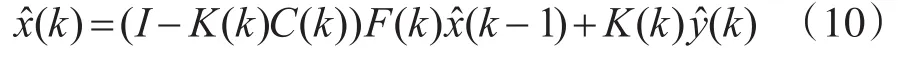
和协方差矩阵

简化结果为

4 实例分析

本文使用下例来说明对于质量数据的处理中卡尔曼滤波的不确定性评估。假设一个水箱在使用过程中满足正弦曲线变化规律，无法直接通过观察精确得出水箱的水位与振幅，并且在进行测量过程中由于仪器失准等外界因素的影响存在误差［9］。此时假设存在关系式

初始的水位为L0=100cm，初始振幅为xs0=0.01cm，频率θ=0.8Hz，导数为

所研究的考虑到误差因素的水位与振幅测量值，目的是用来估计实际水位xl与振幅xs。在研究时间范围内水箱系统水位与振幅的变化表述为如下

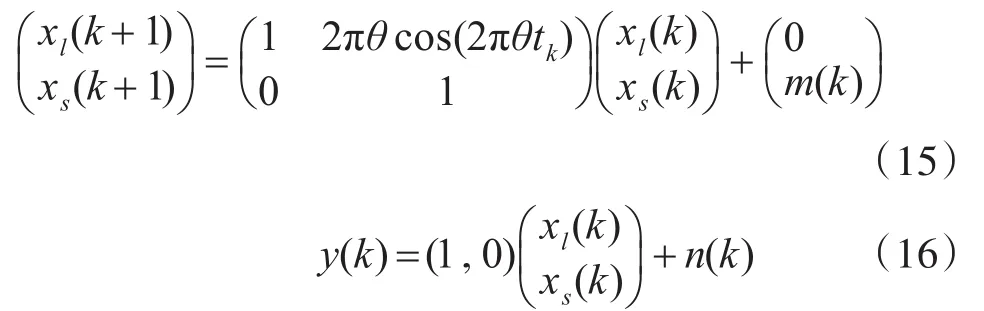
其中状态和测量误差满足 m～N(0，τ2)和 n～N(0，σ2)［10］，标准差 τ=0.01和 σ=1.0 。

图2表示存在误差时随时间推移的水箱系统在假设条件下的水位与振幅变化。可以看到在存在误差情况下，随着振幅的波动变化，水位的变化幅度值也在随之变大变小具有随机性，且变化不具有预见性。现实环境下，在未知实际水位与振幅时，只能通过测量估计得到水位与振幅，本文模拟了一个实际水位与振幅，比较实际水位与振幅和测量得到的水位与振幅的相近程度，目的是用来检验卡尔曼滤波的数据估计水平。

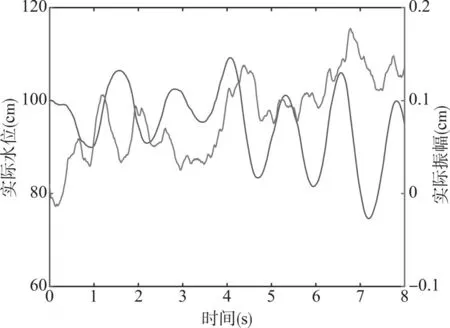
图2 假设条件下系统的水位与振幅

由于测量系统（15）～（16）是具有服从正态分布误差的线性模型，因此可以将线性卡尔曼滤波理论应用于数据评估［11］为

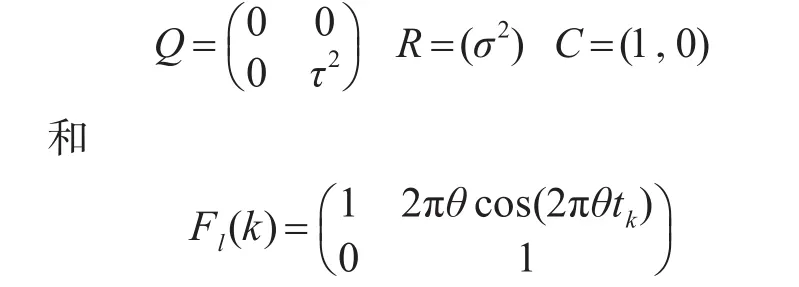
图3为假设条件下系统利用卡尔曼滤波估计得出的测量水位与测量振幅，由图可以看出，由于误差的干扰，卡尔曼滤波方法不断递归估计得出的水位与振幅和实际的水位与振幅产生了一定的偏差，无法呈现为较为直观的线性状态，但是大致变化具有一定的趋向性。

将模拟实际水位与振幅和估计得出的水位与振幅生成在一张图中，结果如图4所示。卡尔曼滤波估计得出的测量水位与振幅和模拟实际水位与振幅较为吻合。在某些时刻，模拟实际水位与测量水位图形几乎重叠一致，在测量区间内，线性整体走势基本一致，估计精度较高。如果要求测量误差方差进一步减小，估计精度将可以进一步改进。

图3 卡尔曼滤波估计的测量水位与振幅

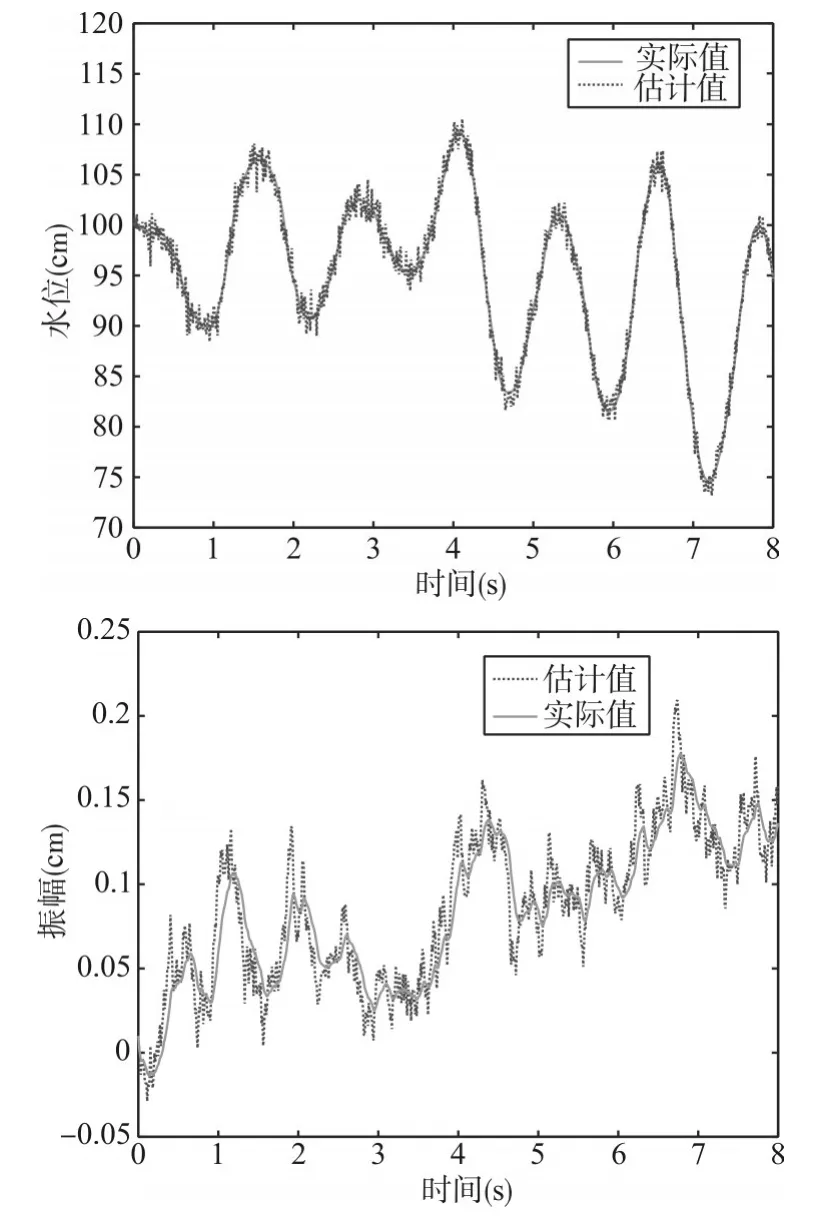
图4 卡尔曼滤波估计结果与模拟系统对比图

实际情况下，当已知系统由于误差等因素的影响使常规测量失准时，无法评估误差对数据的影响程度以及数据的具体变化。此时卡尔曼滤波方法可以很好的评估数据，并且在已知误差服从的规律为高斯分布的前提下，多次对误差递归得到最小方差无偏估计。利用Matlab仿真结果发现无论生成多少次图形，误差对图形影响的情况不同，然而卡尔曼滤波都可以较为吻合的评估数据变化，效果依然很好。

综上通过卡尔曼滤波理论的估计结果，总结卡尔曼滤波突出的优点，可归纳如下：

1）卡尔曼滤波是一套完整的递推算法，特别适合于计算机处理，占内存少，运算速度快，适合实时处理。

2）估计精度高。它是目前已知的估计方法中最好的一种。

3）适应性强。不但适合处理单输入、单输出系统，也适合多输入、多输出系统；适合平稳或非平稳的随机系统，时变过程，稍加推广，也可用来次优估计非线性系统的状态变量。

4）在得到状态变量最优估计的同时，也可得到估计误差的方差阵，可以作为估计精度的一种量度，便于在线监控滤波器的工作质量。

5 结语

卡尔曼滤波理论将被估计的数据看作是线性系统在服从高斯分布误差作用下的输出，并且在时间范围内，线性系统的输入、输出关系由状态方程和输出方程给出，这种特点适用于多输入、多输出的估计问题［12］。将卡尔曼滤波方法用于质量数据评估减少了误差对估计值的影响，因为如果测量误差增大，滤波增益就应该取得小一些，以此减弱测量误差对估计值的影响。

本文利用卡尔曼滤波理论实现一个简单实例质量数据评估的方法——水箱水位与振幅问题。通过研究表明，卡尔曼滤波理论在质量数据评估方面具有较高的研究价值，当由于实际使用情况的特殊和限制因素，无法直观得到装备质量数据时，可以通过卡尔曼滤波理论用来估计装备质量数据当前的大致状态，并将估计精度提高到一定的程度上，便于使用者掌握和了解装备的使用现状，便于评估的进一步开展和进行。此外卡尔曼滤波和状态评估的相关方法在许多领域得到了成功的应用，其按顺序产生了对状态向量的估计，并通过在估计中不断更新的协方差矩阵来刻画其不确定性，适合在质量评估工作准备阶段质量数据处理方面减少不确定性误差对质量数据的影响。