测距码数模混合畸变对北斗导航性能影响分析*

刘瑞华,赵庆田,陈莹超,孔月明

(中国民航大学电子信息工程学院,天津 300300)

0 引言

卫星导航信号是导航接收机发挥导航功能的首要条件,而卫星有效荷载发生故障导致导航信号测距码异常,将会存在难以估量的灾难[1-3]。由于1993年GPS SV19的测距码发生畸变,引起了研究者们关注,并重点研究其畸变模型及对导航性能的影响[4-6]。

研究者们针对测距码畸变现象提出了许多故障模型,ICAO附件10采用了二阶阶跃模型(2nd Order Step,2OS)[5-7]。该模型包括数字畸变模型(threat model A,TMA)、模拟畸变模型(threat model B,TMB)和数模混合畸变模型(threat model C,TMC),其由3个变量决定,即超前/滞后参数Δ、衰减因子σ和谐振频率fd[5-10]。

在系统实际工作过程中,并不是独立发生数字畸变或者模拟畸变的,而是同时存在的[5]。因此文中针对北斗卫星信号测距码的数模混合畸变模型,仿真分析其相关域和频域的特性来研究发生数模混合畸变测距码对北斗导航性能的影响。

1 北斗测距码的TMC模型

数模混合畸变是由测距码生成单元的数字器件与模拟器件二者同时异常产生的,表现为二阶阻尼振荡同时上升沿/下降沿滞后或超前[9],其表达式为[5]:

xTMC(t)=[xnom(t)+xΔ(t)]*h(σ,fd)(t)=xTMA(t)*h(σ,fd)(t)

(1)

式中,xnom(t)理想测距码序列;xΔ(t)为超前或滞后码的部分;h(σ,fd)(t)为模拟畸变滤波器的脉冲响应;xTMA(t)为数字畸变的测距码序列。

当Δ=0.3 chip时,σ=0.8 Np/chip,σ=8 Np/chip,fd=4 MHz和fd=13 MHz不同组合情况下北斗测距码数模混合畸变波形如图1所示。

从图1中可知,测距码下降沿存在延迟,当Δ确定时,σ固定不变,fd越大,测距码抖动频率会越快;fd固定不变,σ越大,测距码抖动幅度趋于平缓的时间越短;并且北斗测距码的TMA和TMB的所有特征均包含于TMC的波形中。

图1 Δ=0.3 chip,不同σ和fd组合下的TMC波形图

2 TMC相关峰分析

相关函数是用来反应任意波形与其自身在时间上偏移之后波形的相似程度,也是导航信号测距码发生畸变所产生伪距误差的直观表现[5]。导航信号测距码发生畸变会使其相关输出的幅值衰减上且相关峰会发生变形[5]。

2.1 TMC的相关函数

TMC的相关函数的数学表达式为[8]:

RTMC(τ,σ,fd,Δ)=Rlag(τ)*h(σ,fd)(τ)=

Rlead(τ)*h(σ,fd)(τ)=

(2)

式中:Rlag(τ)和Rlead(τ)分别是滞后码和超前码的相关函数;E(τ)是单位阶跃响应函数,其公式如下式所示[11]:

(3)

北斗测距码在Δ=0.3 chip时,σ=0.8 Np/chip、σ=8 Np/chip、fd=4 MHz和fd=13 MHz不同情况下的TMC相关峰波形如图2所示。从图中可知,TMC的相关峰曲线存在左右不对称,顶峰处出现平坦区域,且不平滑的现象。表明了TMC相关峰发生畸变会产生测距偏差,那么北斗的导航性能会降低,且增强系统的完好性也随之降低。

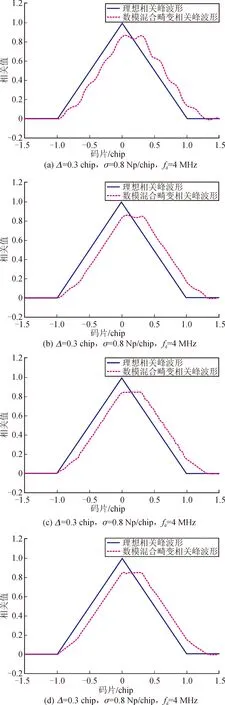
图2 Δ=0.3 chip,不同σ和fd组合下的TMC相关峰

2.2 TMC的相关损耗

理想测距码的相关峰能量与实际测距码的相关峰能量之差称为相关损耗,其中理想测距码的相关峰能量表示为[12]:

PCCF[τ]=20lg{maxoverallτ(|Rnom(τ)|)}

(4)

根据相关损耗的定义可得出其表达式为:

L=PCCF[τ]-20lg{maxoverallτ(|R(τ)|)}

(5)

式中R(τ)是发生异常后的测距码的相关函数。

Δ=0.3 chip时,不同fd和σ值的TMC相关损耗如图3所示。

由图3可知,当Δ确定时,相关损耗值随着fd和σ的增加而增加,最大可达1.411 3 dB。表明了如果相关损耗变大,会降低北斗的导航性能,同时增强系统的完好性也随之降低。

图3 数模混合畸变的相关损耗

3 TMC的功率谱

根据北斗测距码发生数模混合畸变的机理研究其功率谱,然后与理想信号功率谱对比,分析测距码频谱的失真程度。

TMC的功率谱可表示为:

GTMB(ejω)=GTMA(ejω)HTMB(ejω)=

e-jπfΔTccos(πfΔTc)Gnom(ejω)HTMB(ejω)(6)

式中,GTMA(ejω)表示TMA的功率谱,Gnom(ejω)表示理想测距码的功率谱,HTMB(ejω)表示TMB的滤波器频域响应,其公式为[13]:

(7)

图4为Δ=0.3 chip,σ=0.8 Np/chip,fd=13 MHz的北斗导航信号TMC的功率谱。

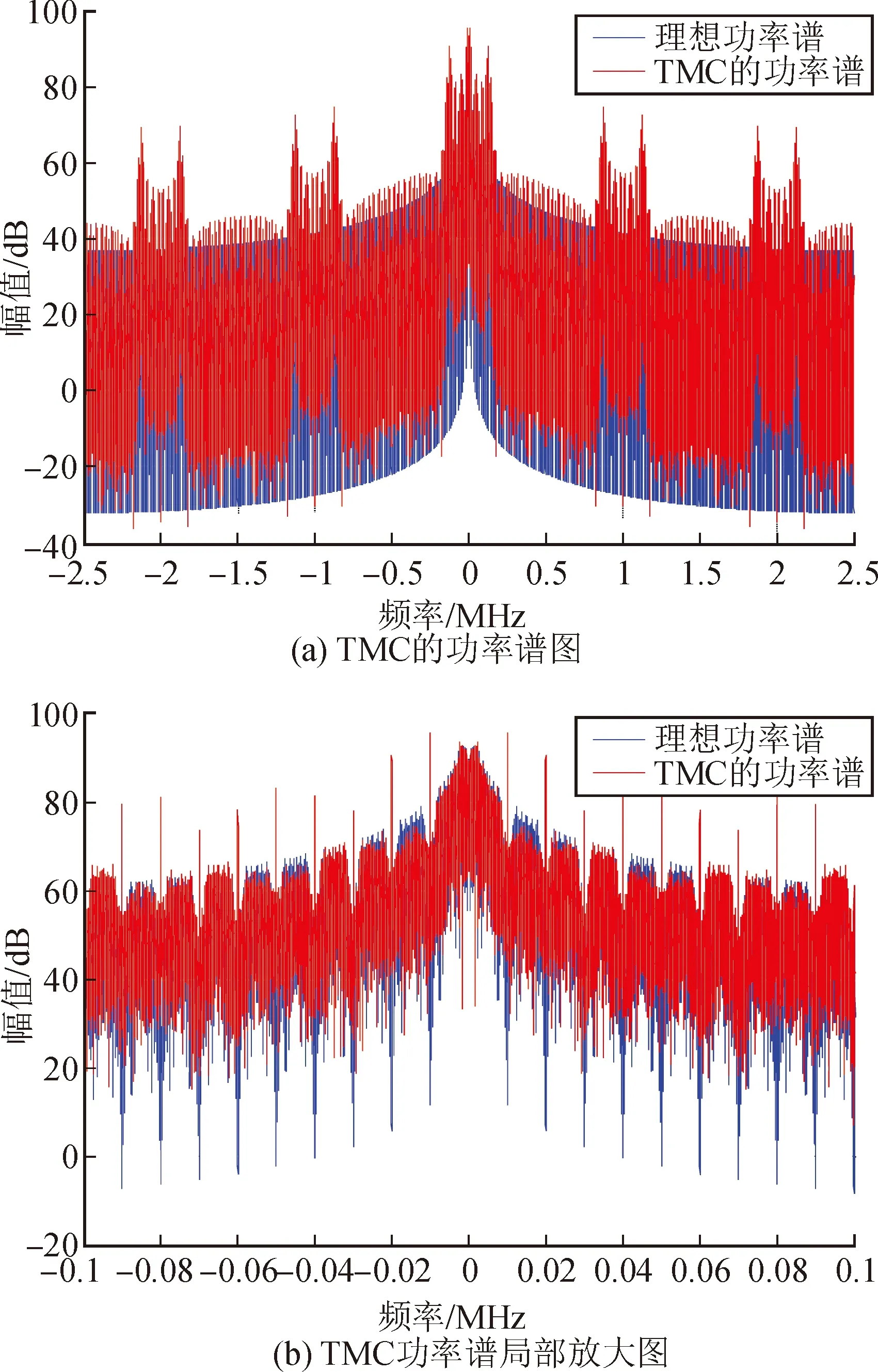
图4 TMC功率谱及局部放大图(Δ=0.3 chip,σ=8 Np/chip,fd=13 MHz)

从图4可知,功率谱的中心频点及左右旁瓣零点处都有不正常的尖峰突起且旁瓣出现衰减现象,即有载波泄漏和功率损耗存在。因此发生数模混合畸变使功率谱存在载波泄漏和功率损耗,那么北斗的导航性能降低,增强系统的完好性也随之降低。

4 TMC对伪距测量的影响

发生异常的北斗测距码会影响其相关峰性能,并且也会使非相干延迟锁定环(DLL)鉴别器码相位的跟踪性能降低[5]。在理想状态下,接收机码环鉴相曲线(即S曲线)是经过(0,0)点的;而测距码发生异常后,S曲线发生了偏移[14]。那么非相干DLL的S曲线数学表达式为[14]:

(8)

式中d表示相关器超前减滞后间距。

锁定点偏差值τbias(d)满足下式:

Scurve(τbias(d),d)=0

(9)

图5为Δ=0.3 chip,σ=0.8 Np/chip,fd=13 MHz时,TMC的S曲线和锁定点偏差;Δ=0.3 chip时,不同σ和fd的伪距测量偏差如图6所示。

从图5(b)中可知,当d=0.04 chip时,TMC的S曲线锁定点偏差值最大,其值为23.5 m。从图6中可以看出,S曲线的锁定点偏差随着fd的变大而增加。因此可得:锁定点偏差与数模混合畸变严重程度成正相关关系,产生了伪距测量偏差,导致对北斗的导航性能及增强系统完好性产生特别严重的影响。

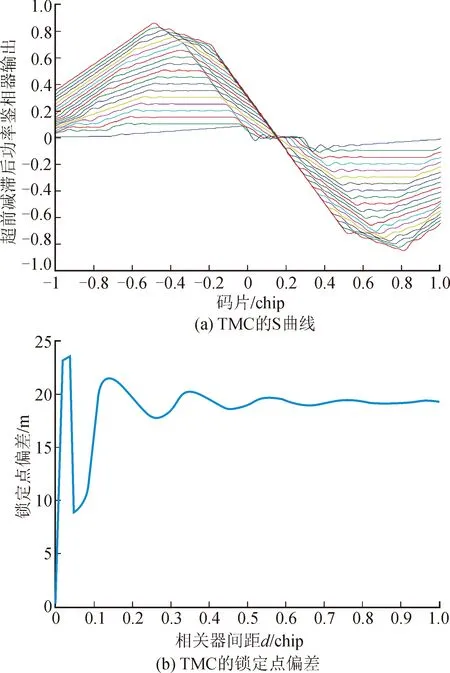
图5 Δ=0.3 chip,σ=8 Np/chip,fd=13 MHz时TMC的S曲线及锁定点偏差

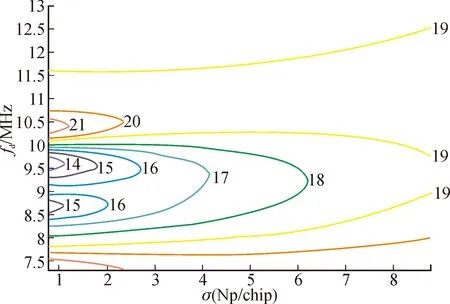
图6 Δ=0.3 chip时,不同σ和fd TMC的锁定点偏差

5 结论

在北斗实际工作过程中,同时存在数字畸变和模拟畸变。那么针对北斗导航信号测距码数模混合畸变的问题,建立了TMC畸变模型并仿真分析了其在相关域和频域内的畸变情况。分析结果表明:数模混合畸变后北斗测距码的相关峰和功率谱均发生畸变,导致伪距测量误差的存在,降低了北斗的导航性能,同时增强系统的完好性也随之降低。