弹道修正火箭弹齐射打击多个目标的方法*

李超旺,文 健,吕 静,曹 永

(1 陆军工程大学石家庄校区弹药工程系,石家庄 050003;2 94608部队,南京 221000)

0 引言

弹道修正火箭弹相对于无控火箭弹来说具有更高的射击精度,打击同一点目标时所需火箭弹数量更少,仍采用传统火力压制方式使用弹道修正火箭弹打击点目标将大大降低其作战效能[1-2]。火箭炮装载火箭弹转移阵地时将会增加行军的危险性,应避免这种情况的发生,此外,通过调整射击诸元的方式打击不同的目标点时将降低火炮的战场生存能力,如何对弹道修正火箭弹进行作战使用还未见相关报道,也没有相关文献研究修正弹齐射时打击多个点目标的可行性及需要解决的关键问题。文中在分析采用脉冲推冲器+阻力板组合修正火箭弹弹道修正特点的基础上,研究了组合修正火箭弹齐射时打击多点目标的方法。

1 工作原理及控制方案

脉冲推冲器具有结构简单、响应时间短和受外界环境影响小的优点,已经在弹道修正弹上得到了应用。阻力板具有较强的纵向修正能力,具有“瞄远打近”的特点,可大大提高火箭弹落角。采用脉冲推冲器+阻力板的组合修正方案能发挥两种执行机构各自的优点,达到提高火箭弹射击精度和大落角打击地面目标的目的,提高火箭弹作战效能。

1.1 组合式弹道修正火箭弹工作原理

组合式弹道修正火箭弹修正系统集成了脉冲推冲器和阻力板两种执行机构,其结构外形如图1所示。

图1 弹道修正火箭弹视图

导航控制舱里面集成有北斗卫星接收机、天线、地磁测量模块、弹载计算机、热电池、脉冲推冲器阵列和阻力板。

火箭弹出炮口以后热电池被过载激活,为整个控制系统供电。卫星接收机实时测量火箭弹的位置和速度信息,弹载计算机将北斗卫星定位信息转化后与标准弹道进行比对,根据建立的落点预测模型解算出弹道偏差,当弹道偏差满足阻力板展开条件或者脉冲激活条件时,发出阻力板展开指令和脉冲推冲器可激活指令,地磁测量模型实时的测量出弹体滚转姿态角,当所选定脉冲推冲器滚转到相应位置时适时激活脉冲推冲器进行弹道修正。

1.2 组合式弹道修正火箭弹控制方案

弹道修正火箭主要用于打击杀伤轻型装甲目标、破坏工事和杀伤敌有生力量。以导弹摧毁目标的概率计算方法为基础,在一定的假设条件下,单发火箭弹摧毁目标的概率P为[3]:

(1)

式中:k为决定于目标抗冲击波能力的系数;q为战斗部装药的TNT当量;σr为火箭弹圆散布均方偏差,近似为纵向均方偏差和横向均方偏差的平均值。

从式(1)可以清楚地看出,当目标确定时,为了达到提高摧毁目标概率的目的,提高射击精度比增加战斗部装药威力更为有效。此外,轻型装甲和防御工事等目标在顶端具有最弱的抗冲击波能力,控制火箭弹以大落角攻击目标能降低目标的抗冲击波的能力,进而提高火箭弹摧毁目标的概率。

为了保证火箭弹打击的高效性,需要提高火箭弹射击精度和控制火箭弹落角。

1.2.1 落点预测导引律

为了利用有限的修正力实现最大程度的弹道修正,需要选择合适的导引律。速度追踪导引律和弹体追踪导引律对弹体过载要求较高[4-6],不适合弹道修正弹,其他一些导引律形式复杂,对于弹体的姿态信息要求较多,这些信息一般难以测得,实际应用比较困难。针对火箭弹弹道性能较好的特点,提出采用基于摄动原理的落点预测导引律。落点预测算法公式如下:

(2)

(3)

(4)

式中:y、z和Vx、Vy、Vz为火箭弹实际位置和速度信息；y0、z0、Vx0、Vy0、Vz0为标准弹道信息；Δy、Δz、ΔVx、ΔVy、ΔVz为同一射程处对应的弹道偏,∂H/∂z、∂H/∂Vz、∂L/∂Vx、∂L/∂Vy、∂L2/(∂Vx∂y)、∂L2/(∂Vy∂y)、∂L/∂y、∂L2/(∂Vy∂Vx)、∂L2/(∂Vy∂Vy)、∂L2/(∂Vx∂Vx)、∂L2/(∂y∂y)为偏导数；ΔH、ΔL为横向、纵向预测偏差值。

为验证预测算法的有效性采用四阶龙格-库塔法对存在初始条件和气动参数误差弹道进行了落点预测仿真试验。试验结果如图2和图3所示。

图2 仿真弹道和标准弹道对比图

从图2可以看出,该条弹道的实际落点在发射系内的坐标为(31 037 m,-151.3 m),相对于目标点偏近了975.5 m,偏右了232.3 m。从图3(a)可以看出,火箭弹飞出11 km左右开始进行落点预测,预测射程较目标射程近700 m左右,而实际落点比目标点近960 m左右,预测误差为260多米,随着射程的增加纵向预测偏差开始收敛,18 km时火箭弹飞过弹道顶点,纵向预测偏差在960 m左右进行波动,与实际值比较吻合,这种状态一直维持到了火箭弹落地。从图3(b)可以看出,横向预测偏差较早就出现了收敛,在11 km处横向预测偏差为227 m左右,实际偏差为232.3 m,偏差只有5.3 m,预测精度较高,随着射程的增加预测偏差略有减小,但是基本保持不变。

从落点预测方法的规律可以看出,在火箭弹到达弹道顶点以前可以对弹道进行方向修正,进入下降段后可以对弹道进行距离和方向的二维修正。

1.2.2 脉冲推冲器修正能力分析

脉冲推冲器的修正能力不仅与冲量大小、工作时间长短和弹体转速有关外,还与工作时间段有关[5]。

由牛顿第二定律知,单个脉冲推冲器作用后在准弹体坐标系内产生的速度增量为:

(5)

ΔVz对于横向修正距离的贡献与剩余飞行时间有关系。对于某一固定弹道,修正时间越早则剩余飞行时间越长,横向修正距离将越大。

纵向修正相对复杂,在上升段,脉冲力作用后,增加了法向速度,但同时减小了纵向速度。法向速度增量ΔVy延长了火箭弹的留空时间,这一延长留空时间引起的纵向修正距离和纵向速度有关,纵向速度越大修正距离越大,反之,则修正距离小。同时,脉冲作用引起的纵向速度减小量缩短了弹体的飞行距离,抵消了部分修正能力。在弹道的下降段,法向速度增量和纵向速度改变对于距离的修正是同方向的,原因分析可以采用上升段的方式。

采用四阶龙格-库塔法对脉冲修正能力进行了仿真计算,单个脉冲推冲器在不同的时间段内对纵向和横向的修正能力对比情况如图4所示。

图4 脉冲推冲器横向、纵向修正能力对比图

从图4中可以看出,脉冲推冲器被激活的时间越早横向修正能力越强,在弹道顶点附近纵向修正能力最强。

1.2.3 阻力板打开控制方法

确定阻力板打开时间较多采用弹道积分的方法[7-8],此方法对于弹载计算机运算速度要求过高。在此提出采用发射前装定阻力板修正能力的方法。

阻力板没有展开时火箭弹有效面积保持不变,阻力板展开以后火箭弹有效面积增加,受到的阻力增大,轴向力系数增加。将阻力板展开以后的全弹轴向力系数代替阻力板没有展开时全弹的轴向力系数,采用龙格-库塔对三条不同的弹道不同时刻展开阻力板时对应的修正能力进行了仿真计算,阻力板修正能力变化、对比情况如图5所示。

图5 阻力板修正能力变化、对比情况图

(6)

从图5可以看出,对于同一条弹道曲线,阻力板打开的时间越晚修正能力越小,但这种衰减的趋势并不是线性的而是类似于开口向上抛物线的左侧。对于不同的弹道,在同一射程处展开阻力板,其修正能力随着无控弹射程的增加而增强,增强的趋势基本为线性,此外,脉冲推冲器可以辅助阻力板进行纵向修正。基于以上分析,提出了发射前根据目标射程解算两条射程扩展量不同弹道的阻力板修正能力,将不同射程打开阻力板对应的修正能力装定到弹载计算机上,火箭弹飞行中,以射程和纵向预测偏差为自变量对阻力板修正能力进行实时插值解算,当阻力板的修正能力小于纵向预测偏差值时发出阻力板展开指令。

1.2.4 不同射程的控制方案

通过对落点预测导引律、脉冲推冲器修正能力特点和阻力板控制方法的分析提出了大射程控制策略:上升段仅用脉冲推冲器进行横向修正,进入下降段以后,如果纵向预测偏差大于0,说明火箭弹实际射程会大于目标射程,可以用阻力板进行纵向修正,脉冲推冲器仅用于横向修正;如果纵向预测偏差小于0,说明火箭弹实际射程会比目标点近,阻力板将没有打开的机会,此时脉冲推冲器不仅要进行横向修正还要对纵向进行修正。

弹道修正火箭弹对近距离目标进行打击时,阻力板主要用于抬高火箭弹的落角。小射程控制策略如下:火箭弹出炮口后立即发出阻力板展开指令,阻力板展开以后火箭弹所受到的阻力加大,以此来控制火箭弹的落角,仅用脉冲推冲器提高射击精度。

2 齐射打击多点目标的方法

从组合式弹道修正火箭弹工作原理可知火箭弹发射前需装定基准弹道,火箭弹飞行中弹载计算机以基准弹道为基础预测落点偏差,可以通过向火箭弹装定不同基准弹道的方法实现齐射打击多点目标的想法。

2.1 打击横向分布多个点目标的方法

火箭弹的基准弹道包括质心的位置、速度信息、发射方向和发射点坐标这四个要素,这四个基本要素确定了唯一的一条基准弹道。火箭弹飞行中弹载计算机接收到卫星定位信息以后,需要将地球坐标信息转化到发射系内才能和基准弹道做差比较,预测出落点偏差。

从地球坐标系到发射坐标系的转换矩阵为:

速度矢量从地球坐标系到发射坐标系的转换关系为:

(7)

位置坐标分量从地球坐标系到发射坐标系的转换关系为:

(8)

(9)

(10)

式中:λ0、B0、A0为发射点经度、纬度和基准射向;Rxe0、Rye0、Rze0为发射点的地心矢径在地球坐标系上的分量;xe、ye、ze为火箭弹质心的地心矢径在地球坐标系上的分量;N为发射点的卯酉圈半径;αe为地球赤道半径;e为地球第一扁心率。

从式(6)～式(10)可知,对于确定发射点的火箭弹来说,基准射向确定以后坐标转换关系唯一确定。可以通过改变射向的方法,确定不同的目标点的基准弹道。原理如下:

如果目标点1(简称点T1,下同)在OX方向上,如图6所示,根据气象信息和发射点、目标点坐标可以解算出来火箭弹的基准射向。假设基准射向与OX轴的夹角为A0,火箭弹沿OA方向进行射击,不出现扰动时火箭弹将沿基准弹道(即图6中的虚线)飞行,直至命中目标。

假设炮目之间的距离OT1为30 km,对于垂直于OX轴的T2来说,如果T1T2为300 m,按照三角形之间的关系可得OT2为30.001 5 km,按照弹道修正弹对于精度的要求指标来说完全可以忽略这点差别。可以将装定到打击T1点火箭弹上的基准弹道位置、速度信息照搬到OT2上,OT1与OT2之间的基准弹道只有射向不同,OT2对应的基准射向在OT1基础上需向右调整,根据三角函数关系可得所需调整角度为:

同理可以解算不同目标点对应的基准弹道。

图6 横向分布点目标与炮位之间对应关系示意图

由于弹道修正弹修正能力有限,可以用处在横向分布几何中心的目标点计算射击诸元和基准弹道,其他目标点的基准射向可以采用目标点之间的三角函数关系解算出来。火箭弹发射前可按目标的急需程度或者目标的抗冲击波的系数将基准弹道信息和对应的射向分配到填装的各发火箭弹上,弹载计算机会根据发射点坐标和装定的射向将卫星定位信息转到对应的发射系内,进行弹道偏差的解算,形成弹道修正指令,控制执行机构作用改变火箭弹的受力分布修正弹道,将火箭弹导引到目标点附近。

2.2 打击纵向或均匀分布多个点目标的方法

火箭弹打击纵向分布或均匀分布目标点时,由于射程差距较大,如图7所示,打击不同目标点时其基准弹道将有较大差别,将不能沿用打击横向分布多个目标点的方法,对于每一个目标点都需要重新解算基准弹道和控制参数。基准弹道解算方法同打击单个目标点的方法相同,不同之处在于由于每个目标点的坐标不同,需要多次解算基准弹道。

组合式弹道修正火箭弹具有较强的“打远修近”能力,但是修远能力不强,射击诸元需要以炮位和最远处目标之间的距离为输入量进行解算。将基准弹道和对应的射向按需分配装定到火箭弹上进行射击即可。

图7 纵向排列目标点与炮位之间的关系

火箭弹打击区域均匀分布多个目标点时可以采用同样的方法。

3 仿真结果与分析

为了验证方法的可行性和有效性进行了火箭弹齐射打击不同点目标的数学仿真试验,假设脉冲推冲器冲量为18 N·s。通过四阶龙格-库塔法进行积分解算,其中气动系数和气动系数导数以马赫数和攻角为输入量通过线性插值获取,脉冲推冲器和阻力板作用时在相应的弹道方程里面增加力或力矩量。

试验1:打击横向分布多点目标的情况

假设有5个目标点在火炮的正前方呈横向排列,相邻目标点之间的距离为100 m,中间目标点与火炮之间的距离为30 km,火箭弹发射条件为标准气象条件,火箭弹发射时受到的随机干扰均值见表1,误差均值乘以幅值为1且服从正态分布的随机数作为仿真输入量。按照弹道修正火箭弹打击横向多点目标的方法计算了射击诸元和5个不同的目标点的装定诸元,认为这5个目标点同等重要,对每个目标点都进行了80次弹道修正模拟打靶,所有400条弹道落点与相应目标点之间的仿真实验结果如图8所示。

表1 初始条件和气动参数误差均值

图8 齐射打击横向排列多个目标点仿真结果

从图8可以看出,对5个目标点同时进行打击时,火箭弹能够按照装定的基准弹道和控制参数进行弹道修正,火箭弹实际落点都在相应目标点附近。经修正后纵向偏差极差控制在50 m以内,横向散布相对较大,少数火箭弹落点与相应目标点之间的距离达到了80 m左右,纵向密集度明显好于横向。此外,从图中还可以发现,对中间目标点进行射击时密集度最好,但是随着目标点散布的增加,火箭弹落点散布略有加大,这有可能是横向修正能力不足的原因。

试验2:打击纵向或均匀分布多点目标的情况

假设有5个目标点在火炮的正前方呈纵向排列,相邻目标点之间的距离为100 m,最远目标点与火炮之间的距离为30 km,火箭弹发射条件及受到的随机干扰平均值与试验1相同,也通过随机数的形式加入到弹道方程里面,所有400条模拟打靶仿真实验弹道落点和相应目标点的对比情况如图9所示。

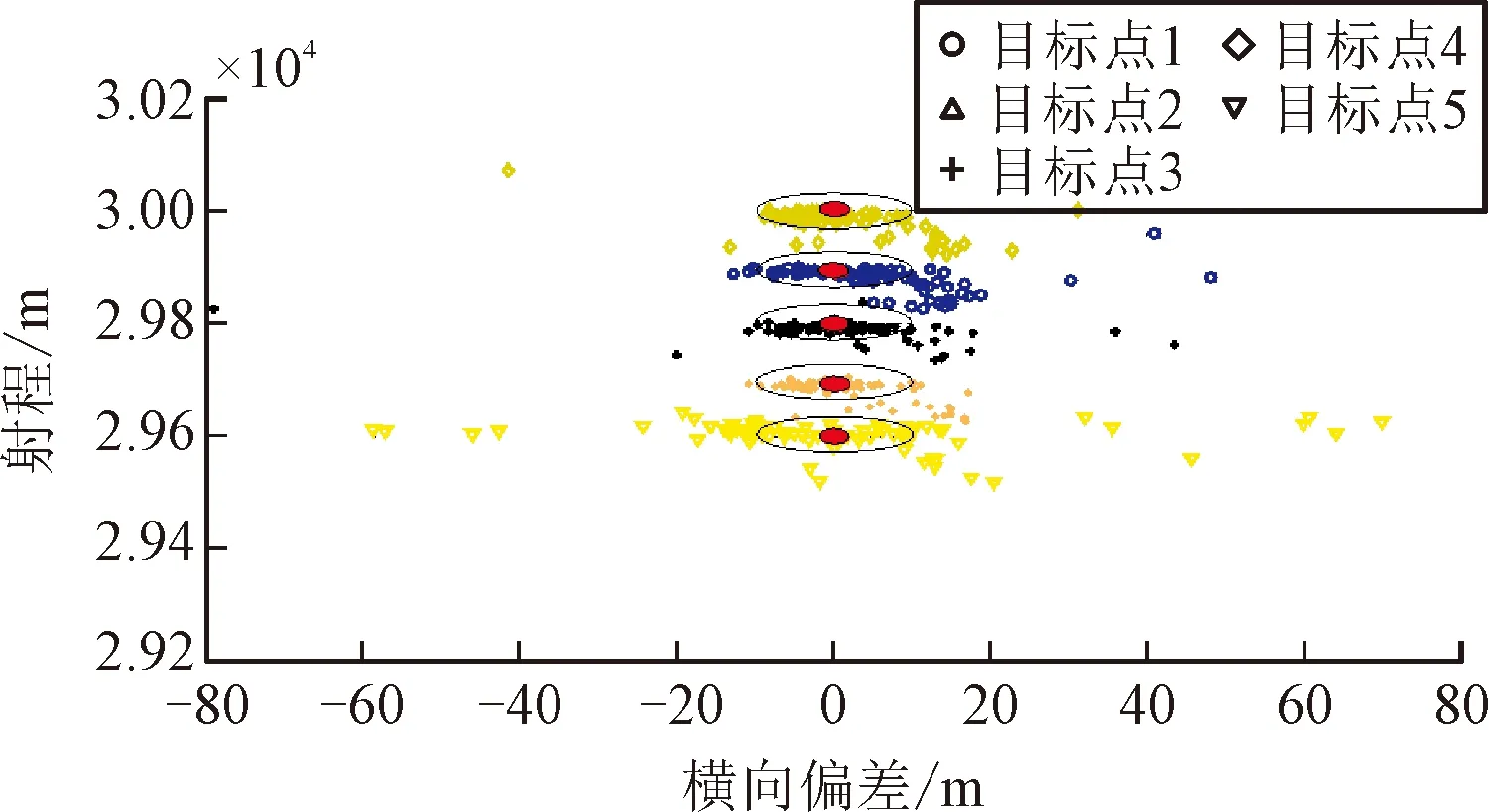
横向偏差/m图9 齐射打击纵向排列多个目标点仿真情况

从图9可以看出,火箭弹齐射时能对纵向排列的5个目标点实现分别打击,对于每个目标点都具有较高的精度。随着目标点与瞄准点之间的距离增加,弹道修正效果有所变差,但仍完全满足火力打击对于弹道修正火箭弹的射击精度要求。

4 结论

目前,对于弹道修正火箭弹的研制取得了很大的进步。文中在分析组合式弹道修正火箭弹控制方案的基础上首次提出了火箭弹齐射时分别打击不同目标点的方法,介绍了打击典型形状排列目标点的技术原理和实现方法,仿真实验结果验证了火箭弹齐射分别打击不同目标点的可行性和有效性。文中所提方法对于进一步增强弹道修正火箭弹作战效能,增大对敌目标的打击能力,具有重要的理论支撑。火箭弹齐射分别打击不同点目标的方法对于火箭弹弹道修正能力有一定的要求,如何充分利用有限的修正能力来达到最佳修正效果是今后需要解决的一个重要问题。