空调通风系统管道气动噪声分析
2018-08-27,,,
,,,
(武汉理工大学 a.能源与动力工程学院;b.高性能船舶技术教育部重点实验室; c.船舶动力系统运用技术交通行业重点实验室,武汉 430063)
目前针对船舶通风空调系统噪声的研究,一部分是根据传统经验算法估算出噪声再结合实验测量数据进行声学设计和降噪处理[1-3];或者从模态分析的角度来处理舱室内装对船舶空调舱室内部复杂结构的影响,并据此对舱室进行声学预报与设计[4-5];还有利用有限元法(FEM)、边界元法(BEM)和计算流体动力学(CFD)相结合的手段来预测船舶空调系统的噪声[6-8];针对通风系统气动噪声,大多考虑风机噪声的影响[9-12],而考虑管道噪声对空调舱室影响的声学设计研究较少。针对管道气动噪声对整体通风空调系统的噪声水平的影响问题,拟采用CFD流体动力学仿真和FEM有限元声学仿真相结合的方法,分析管道噪声的生成原因、变化规律和抑制手段。
1 计算模型
1.1 空调通风管系布置
管道噪声是由于管道内流动的气体在经过弯头、三通、变径管、阀门和送回风口等截面积变化部位产生涡流、涡阻现象引起结构振动产生噪声,尤其当管道里有异物(如导流片、支架、梁柱等)时,空气经过会形成压力脉动变化,等同于多个偶极子声源辐射噪声。因此,空调通风管系的结构布置直接影响着管道噪声的大小。
以本校辅机实验室中船用中央空调系统为研究对象,该系统采用的是二段式制冷工作原理,其管道结构比一般空调通风系统更加复杂。系统组成及工作原理见图1。

图1 空调系统原理
1.2 管道建模和网格划分
使用Pro/E建立空调通风管道流体域模型,利用ANSYS ICEM CFD对其进行四面体网格划分。对于线性有限元模型通常要求最小波长内有6个单元,故对于最大分析频率2 000 Hz,单元长度不应大于28.33 mm。模拟仿真过程中发现,直管等湍流强度不大的区域可以减低对网格密度的要求,为了使网格数量尽可能减少,同时保证计算精度,将流体域模型分成3个区(见图2),分别为弯管三通变径管的部分(WALL_1)、布风器的部分(WALL_2)和直管的部分(WALL_3)。三部分网格尺寸定义不同,最终CFD网格总数为741 236。同时,因为声学计算网格对网格密度的要求要低于CFD计算网格,故以CFD网格为基础,修改网格尺寸,划分出声学网格,其网格总数为388 518。CFD网格和声学网格所选取的具体网格尺寸见表1。

图2 管道流体域网格

类型区域网格尺寸/mm最终网格数CFD网格WALL_1WALL_2WALL_3301560741 236声学网格WALL_1WALL_2WALL_3402080388 518
2 数值计算理论
2.1 标准k-ε湍流模型
根据其流体高雷诺数的特点,选用标准k-ε湍流模型。标准k-ε模型是半经验公式,主要基于湍流动能和扩散率。其湍流能k和湍流耗散的输运方程如下[13]。
Gk+Gb-ρε-YM+Sk
(1)
(2)
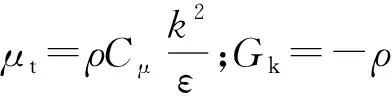
2.2 分离涡(DES)湍流模型
使用CFD进行瞬态计算时,通常使用大涡(LES)湍流模型或者分离涡(DES)湍流模型,但是LES在用于模拟高雷诺数的边界层流动时,对计算网格的要求十分严格,对计算机高性能的要求可能会导致计算进展缓慢甚至无法顺利进行。分离涡流模型(detached eddy simulation,DES)结合RANS和LES各自的优势,可大大降低对计算网格的要求。其含能尺度l和k的输运方程为[14-15]
(3)
(4)
式中:Δ为最大的网格尺寸,Δ=max(Δx,Δy,Δz);CDES=1.3。
2.3 气动声学理论
气动声学(aeroacoustics)由Lighthill研究喷气噪声开始,经Curle、FfowcsWilliams和Hawkings的补充发展,已经形成了一套完整的理论体系[16]。从流体力学N-S方程中推导出的Lighthill方程为
(5)
导入格林函数
(6)
得到式(5)的解,再考虑上固体壁面的气动声学声类比方程,进一步推导,得到远场声压解。
(7)
方程右边第一项为四极子声源,代表由空间湍流引起的四极子噪声,当气流马赫数较低时,不用考虑在内;第二项为偶极子声源,代表由固体壁面压力脉动引起的偶极子噪声,是固定结构表面的主要气动噪声源。
3 计算及结果分析
3.1 计算分析流程
在气动噪声计算中,采用Fluent联合LMS Virtual.Lab Acoustics对空调通风管道声场进行求解。首先利用Fluent对流场进行稳态计算,在计算收敛之后以此为初值进行瞬态计算;然后以CGNS文件形式输出时域计算结果;接下来在LMS Virtual.Lab Acoustics里将时域数据转化为频域结果,相关流程见图3。
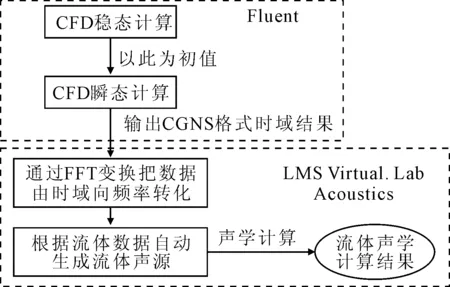
图3 气动噪声计算分析流程
3.2 CFD多物理场仿真计算分析
在ANSYS FLUENT中选用压力求解器,速度方程选用绝对速度。2个入口为速度入口边界条件,计算空调房间的冷负荷和散湿量,根据湿空气焓湿图推导送风量[17],得到入口1的速度为2.303 m/s,温度为7 ℃,入口2的速度8.444 m/s,温度为14 ℃。4个出口为压力出口边界条件,设总压均为0。稳态计算选用标准k-ε湍流模型,速度与压力耦合方法选用SIMPLE算法。再以稳态计算结果为初值进行瞬态计算,改用DES湍流模型和PISO算法,时间步长设为0. 25 ms,时间步数选为1 000次。
在流场中,湍流形成的涡流在固定壁面处会产生压力脉动,将这种压力脉动等效成多个壁面偶极子的形式。流场中涡核的分布见图4。

图4 涡核分布
从图4可以看出,由于左边入口1的流速较慢,而右边入口2的流速较快,导致右边的弯管处的涡核分布比左边密集,直管处基本没有涡核分布,这是由于这些位置近似是层流状态。值得注意的是,在4个布风器处涡核分布很集中,说明2股气流在布风器中混合将产生大量湍流运动,而这种湍流的出现是造成噪声的主要原因之一。2个入口和4个出口的平均温度、压力、流速值见表2。

表2 出入口物理量平均值
通风管道相关物理量体渲染图见图5。

图5 流体多物理量体渲染图
模拟结果显示,在各个布风器出口处存在较大负压区,并且形成了气流漩涡。漩涡对布风器出口处的气体输送产生了不利的影响,甚至出现了回流的现象,这会造成更大的压力脉动和能量损失,进而诱发噪声。从流速图可以看出,除了弯管处的流速会短暂提高外,布风器负压区的速度变化巨大,将产生很大湍流区,进而对气流产生阻滞现象,也正是因此形成了压力图中显示的漩涡。
3.3 流体声学仿真计算分析
将瞬态计算得到的CGNS格式管道壁面压力脉动的时域计算结果导入LMS Virtual.Lab中进行快速傅里叶变换。由于在CFD计算时选用的时间步长为0.25 ms,且在时域上采集了1 000步,因此实际的物理时间为0.25 s,频率分辨率为4 Hz。同时得到采样频率为4 000 Hz,根据采样定律对应的最大分析频率为2 000 Hz。
通风管道的声学计算网格见图6,出口处的椭圆半球网格是自动匹配层(AML)。十字交叉网格是设置的场点网格,不参与计算,可以从中提取辐射声场数据,A是场点网格上的I/O Point,声学计算后可以得到该点的频率响应。
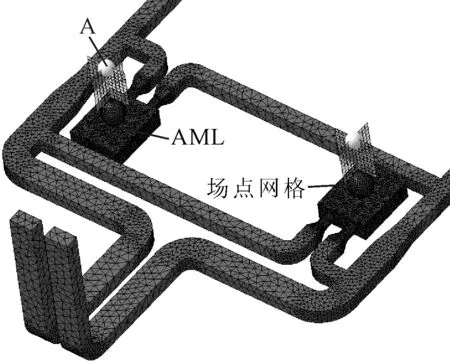
图6 声学计算网格
各出口声压级频率响应见图7,出口编号与图4所示相同。

图7 各出口场点声压级频率响应
可以看出各出口的声压级峰值均集中在72 Hz附近,入口速度小的一侧的出口1、4的峰值约为50 dB,而入口速度大的一侧的出口2、3的峰值为60 dB。可以看出空调系统的气动噪声主要集中在中低频部分,而高频部分的声压级平均值在10 dB附近。从图8中观察到出口1、2峰值频率下辐射声场的声压,可以看出各出口声压分布情况十分契合频率响应曲线所捕捉到的声压级峰值。
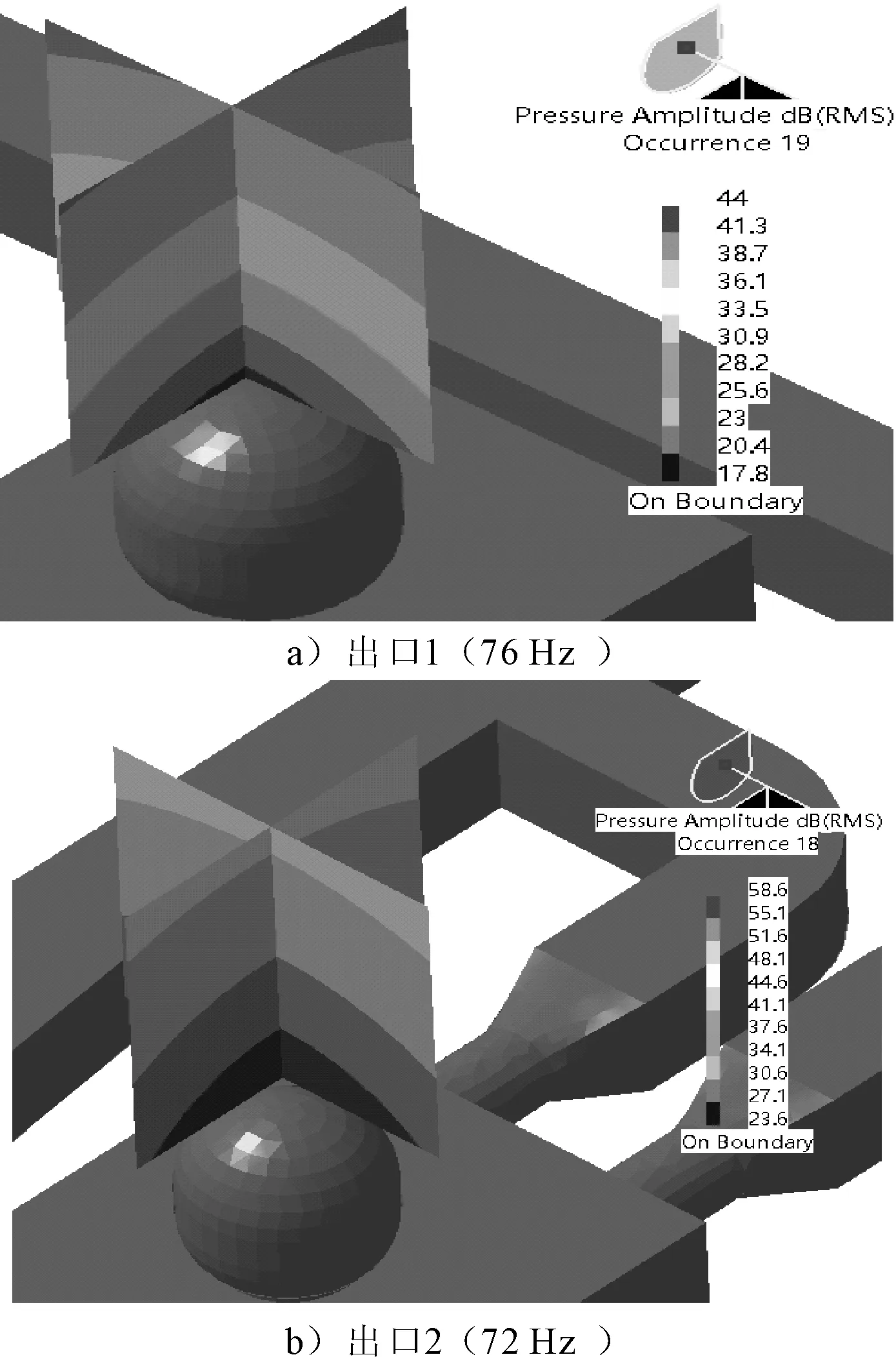
图8 出口1、2峰值频率下得到场点声压云图
由图7和图8作如下判断。
1)通风管路流场的气动噪声频带较宽,除了在低频68到76Hz间有峰值外,没有其他明显的主频率,可以视为一种宽频噪声。
2)4个观测点的声压级幅值都在低频时较大,随着频率升高,幅值有不同程度下降,认为通风管路流场气动噪声主要能量集中在中低频部分。
3)各布风器都由2个不同速度入口进风混合,但较高速度入口侧的测点声压级幅值明显高于另一侧,说明管道流速对气动噪声的影响较大。
4 结论
1)由流体运动引起的脉动压力在壁面上形成的壁面偶极子声源是管路噪声的主要来源。
2)分析管道内部流场可以十分直观地观察到弯管和布风器处的涡流分布状态,而这些不规则的湍流运动造成局部的高压低压区,是形成紊流回流现象,造成气动噪声的主要原因。
3)通风管道气动噪声是宽频噪声,主要噪声能量集中在中低频部分。
4)气动噪声源最强的区域并不完全和流速最大的区域一致,说明除了流速外,通风管道的结构形式,会产生另外的压力脉动,从而对气动噪声的分布情况产生影响。
5)分析主要针对空调通风系统管路气动噪声在0~2 000 Hz内的声压频谱;实际上系统的气动噪声还有另一个主要来源,即离心风机噪声,有必要综合考虑离心风机流场及声场和管道噪声,这部分工作有待深入研究。
