基于多体系统传递矩阵法的四旋翼飞行器振动建模

范肖肖，贺嘉璠，戚国庆，李银伢，盛安冬

（南京理工大学自动化学院，江苏南京210094）

在四旋翼飞行器的控制问题研究中，建模方法通常是将四旋翼飞行器简化为刚体，从整机受力出发，基于牛顿第二运动定律及欧拉方程建立动力学模型[1-3]。然而依据实际情况，此类模型未考虑系统的固有频率，在飞行中四旋翼飞行器受到固有频率附近的周期激振力时，容易产生共振现象。目前对四旋翼飞行器振动的研究相对较少，共振的研究主要集中在航天器、直升机这类飞行器中[4-6]。文献[4]针对共轴铰接式旋翼直升机，提出时—频分析法研究上下旋翼摆振和机体运动间的耦合，揭示共轴式直升机地面共振的物理机理。文献[5]采用传递矩阵方法对直升机旋翼试验台传动系统的振动特性进行分析。文献[6]针对含有大型柔性附件的航天器，用有限元分析软件与MATLAB联合分析系统振动模态。在飞行过程中四旋翼飞行器也会受到外界的气流干扰，当扰动频率接近飞行器的固有频率时，容易引起共振，从而影响飞行器姿态的稳定性。如果不能对其振动特性尤其是固有频率进行准确求解，往往难以设计出动态性能良好的控制器，因此对四旋翼飞行器的振动特性进行准确表征有着重要的意义。

经典的有限元分析法虽然具备对旋翼类飞行器进行模态分析的能力，但旋翼类飞行器结构复杂，采用有限元法存在计算规模大、运算耗时长等问题。多体系统传递矩阵法在自行火炮发射动力学、多管火箭发射动力学与舰炮发射动力学等工程领域的成功应用验证了该理论的有效性[7-9]，其中线性多体系统传递矩阵法[10]特别适用于复杂多刚柔体系统的振动特性求解，该方法由于涉及的矩阵阶次低从而避免了复杂多刚柔体系统振动特性计算病态，保证了系统特征值的快速求解[11]。

文中基于线性多体系统传递矩阵法，建立四旋翼系统每个元件的传递矩阵以及系统总传递矩阵。在MATLAB上求解特征方程，获得系统的固有频率，并且通过实验验证固有频率求解的准确性。在此基础上，修正了四旋翼飞行器未考虑系统谐振模态的常规模型，提出一种带有谐振模态的四旋翼飞行器动力学模型，对后续控制器设计中抑制共振现象有实际意义。

1 振动特性求解

1.1 结构分析

本文研究的四旋翼飞行器系统为常见的十字形对称布局，简化的三维模型如图1所示。根据其结构特点，四旋翼飞行器可视为四端输入一端输出的空间振动多刚柔体[12]。应用线性多体系统传递矩阵法的思想，可推导出该模型输入与输出之间的关系，即得到传递方程和传递矩阵。

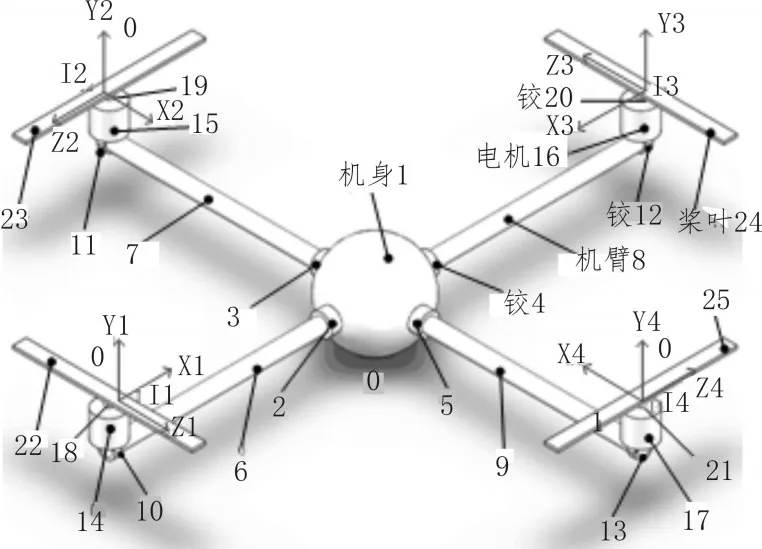
图1 四旋翼飞行器简化模型

根据四旋翼飞行器的结构特征，将其划分为若干部件并依据各个部件的特性，进行简化处理。机身简化为刚体元件，机身的弹性效应等效为空间弹性铰元件。机臂等效成Euler-Bernoulli弹性梁元件[12]。驱动电机简化为刚体元件，驱动电机与机臂之间的联接简化为空间弹性铰元件。根据多体系统传递矩阵法“体”元件和“铰”元件统一编号的原则，将各元件分别编号，系统边界均编号为0，元件的简化方式及编号见表1。

根据线性多体系统传递矩阵法的原理[12]，该多刚柔体系统有4个输入端，分别为桨叶22、桨叶23、桨叶24、桨叶25；机身1的中心为系统的输出端，沿输入端到输出端的方向即为系统的传递方向。沿着传递方向，进入元件的点称为输入点，用I表示，传递完成后，离开元件的点称为输出点，用O表示。在每条传递路线上元件之间的联接点不仅是前一元件的输出点，也是后一元件的输入点，用Pi，j表示该节点，其中i表示体元件的编号，j表示铰元件的编号。

表1 元件简化方式及编号

1.2 状态矢量

图1中的四旋翼系统含有24个联接点和5个边界点。其中联接点依次为P1,i(i=2～5) 、Pi,i-4(i=6～9,14～17,22～25) 、Pi,i+4(i=6～9,14～17) ，5 个边界点依次为P0,22,P0,23,P0,24,P0,25,P1,0。定义各点的状态矢量如下

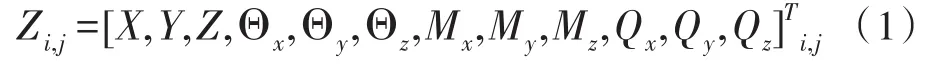
其中各状态变量分别用来表示各点在模态坐标下的线位移、角位移、内力矩和内力[12]。其中状态矢量Z0,22、Ζ22,18、Z14,18、Z14,10、Z6,10、Z6,2、Z1,2、Z1,3、Z1,4、Z1,5、Z1,0定义在I1x1y1z1坐标系内，Z0,23、Z23,19、Z15,19、Z15,11、Z7,11、Z7,3定义在I2x2y2z2坐标系内，Z0,24、Z24,20、Z16,20、Z16,12、Z8,12、Z8,4定义在I3x3y3z3坐标系内，Z0,25、Z25,21、Z17,21、Z17,13、Z9,13、Z9,5定义在I4x4y4z4坐标系内。

1.3 传递方程

1.3.1 空间振动刚体

桨叶22～25和驱动电机14～17均为单端输入单端输出的空间振动刚体，传递方程为：

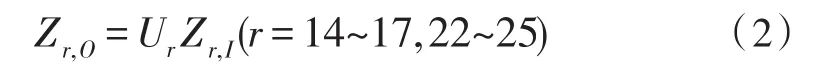
传递矩阵为：

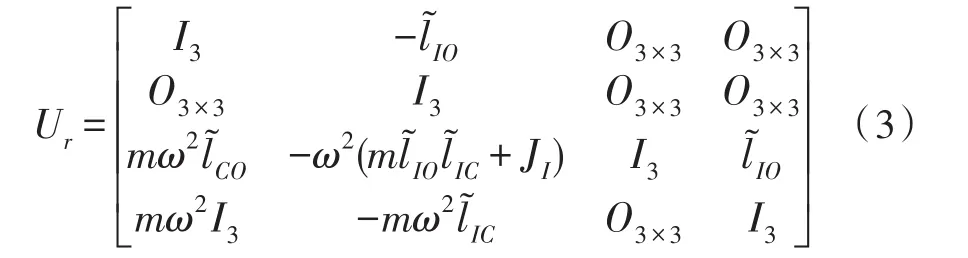
其中m为刚体的质量；在以输入端I为坐标原点的连体坐标系中，JI为刚体相对输入点I的转动惯量矩阵，lIO为刚体输出端相对I点的位移，lIC为刚体的质心相对I点的位移，分别为lIO和lIC的叉乘矩阵。

机体1为四端输入一端输出空间振动刚体，令P1,r+1(r=1～4)为第r输入点Ir，则从输入点P1,2～5到输出点P1,0的传递方程为

在以输入端I1为原点的连体坐标系中，为刚体相对I1点的传动惯量矩阵，lIrO为刚体输出端相对其它输入端Ir的位移，是其叉乘矩阵。Hα、Hβ、Hϕ分别为坐标系I2x2y2z2、I3x3y3z3、I4x4y4z4到I1x1y1z1的坐标变换矩阵[12]。

1.3.2 空间弹性铰

元件 2～5，10～13，18～21为空间弹性铰，传递方程为：

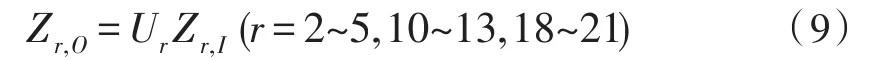
传递矩阵为：

式中

Kr,x、Kr,y、Kr,z分别为弹簧在x、y、z3个方向的弹性刚度，分别为扭簧在x、y、z3个方向上的扭转刚度。

1.3.3 空间弹性梁

机臂6，7，8，9为空间振动弹性梁，考虑x轴、y轴、z轴的横向空间振动，其传递方程为：

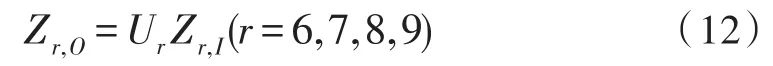
式中，Ur∈ℝ12×12，除了以下说明元素，Ur中的其余元素均为零：

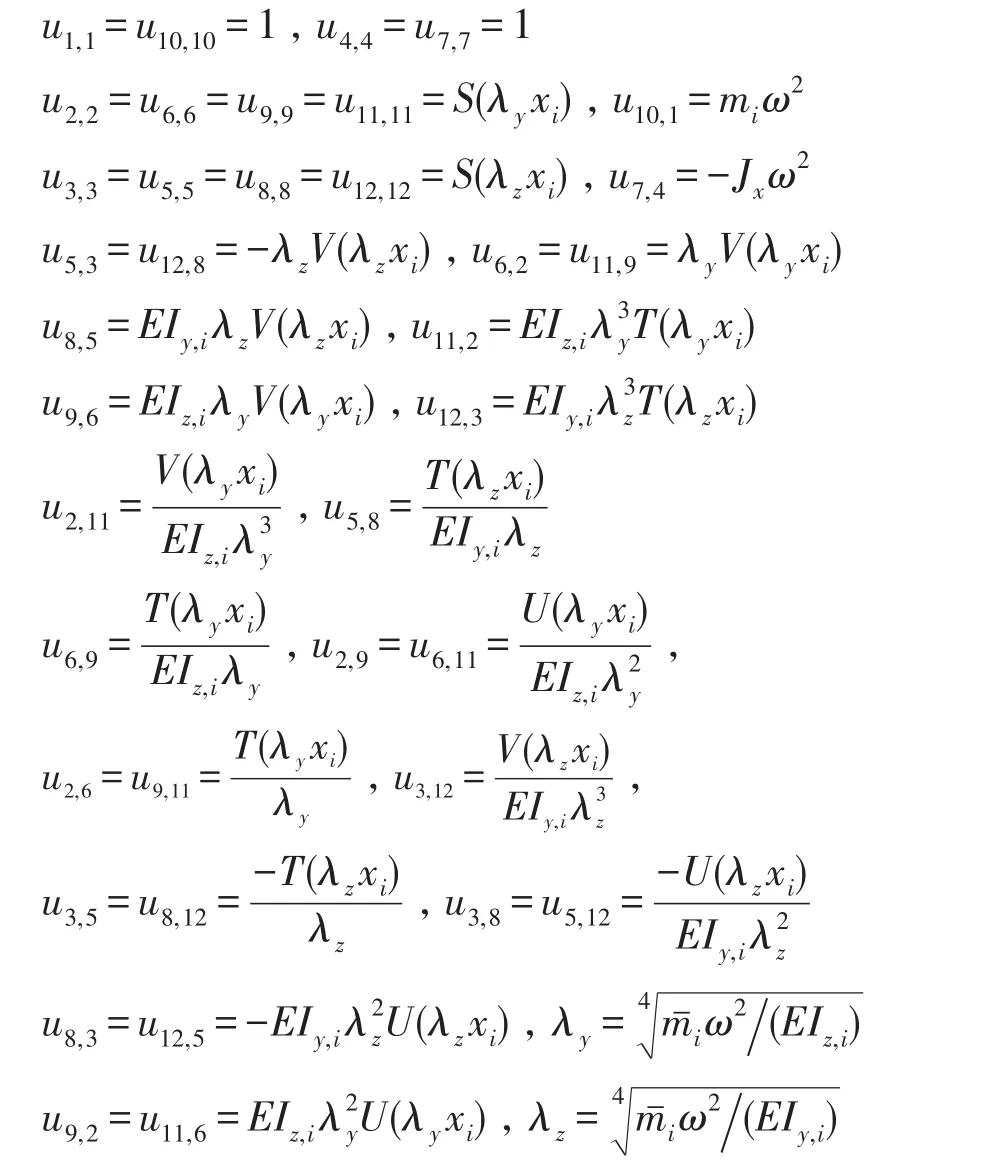
式中：0≤xi≤li，ρ为梁的密度，为梁的线质量密度，Iy,i、Iz,i为截面的惯性积，E为弹性模量，li为梁的长度。S(x)、T(x)、U(x)、V(x)

为 Крылов 函数[12]。

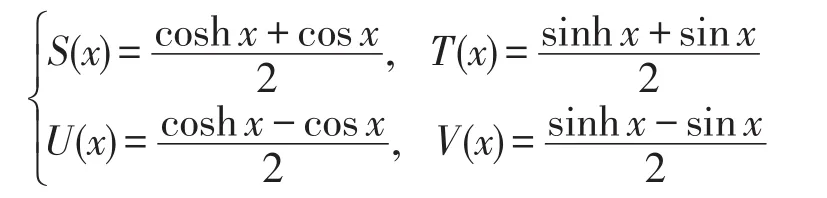
1.3.4 系统总传递矩阵

根据文献[13]中多体系统传递矩阵法总传递方程的推导定理，可推导出四旋翼飞行器系统的总传递方程为：

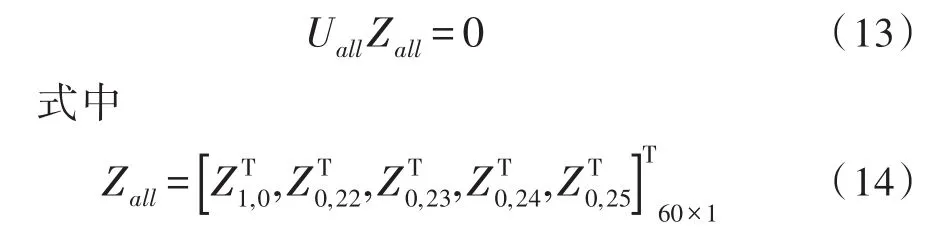
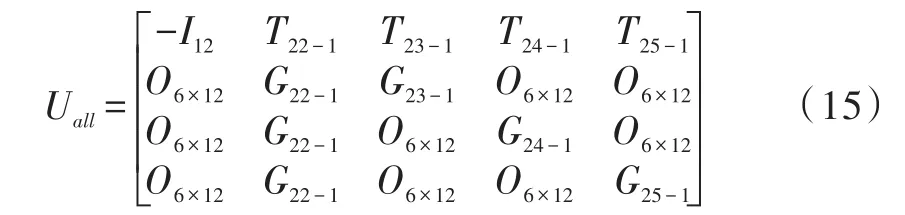
分别为四旋翼飞行器系统边界点组成的状态矢量和系统总传递矩阵，并有：

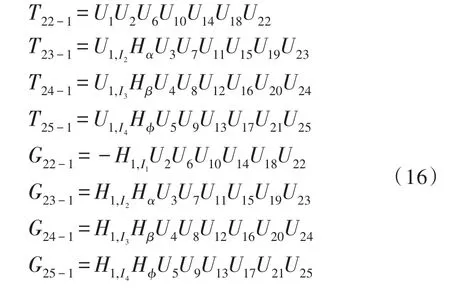
1.4 固有频率求解

利用多体系统传递矩阵法，拼接各元件的传递矩阵得到系统总的传递矩阵，代入边界条件得到系统的特征方程，对其求解即可得到系统的固有频率。

不加任何外部激励的情况下，对四旋翼飞行器系统进行自由振动分析，桨叶和机身输出端均为自由端，边界条件表示如下：

将边界条件带入总传递方程，删除状态矢量Zall中的零元素记为，删除状态矢量Uall中对应零元素的行和列记为，改写式（13）为如下形式：

从以上过程可知，和Uall都只与系统自身的结构参数及固有频率ωk(k=1,2,3…)有关。对于实际的四旋翼飞行器系统，方程（19）必有非零解，则系统的固有振动频率ωk(k=1,2,3…)对应的矩阵Uˉall需满足下面的条件

式（20）即为系统的特征方程。求解特征方程得到四旋翼飞行器系统的固有振动频率[14]。

2 数值仿真与实验

2.1 固有频率仿真与分析

对四旋翼飞行器振动分析能够指导后续控制系统的设计，更好地抑制共振，从而提高四旋翼飞行器姿态控制系统的性能。

基于实验室现有的四旋翼飞行器实验平台，得到四旋翼飞行器各部件的主要参数如表2所示。在线性多体系统传递矩阵法对四旋翼飞行器进行模态分析的基础上，结合MATLAB计算得到系统的各阶固有频率，如表3所示。可以看出，前10阶振动模态分布在12.3～5131.3 Hz之间，一阶固有频率最低，固有频率随着模态阶数的升高呈递增趋势。固有频率越低，越容易激发出相应的模态发生共振，因此工程上着重考虑低阶固有频率。

表2 四旋翼飞行器的主要参数

表3 四旋翼飞行器振动各阶固有频率

2.2 四旋翼飞行器振动实验与分析

为验证固有频率求解的正确性，对四旋翼飞行器进行实验研究，实验平台如图2所示。采用F450四轴飞行器，配有ArduPilot Mega自动驾驶仪，通过地面控制站Mission Planner读取MPU6000加速度传感器，得到飞行过程中的姿态信息。

图2 四旋翼飞行器实验平台

实验过程中调节油门的大小来改变电机的转速，从而使四旋翼飞行器在不同的频率下工作。为了降低外界环境对实验的干扰，在室内环境下，缓慢增大油门使旋翼转速逐渐升高，得到四旋翼飞行器在机体坐标系下X、Y、Z3个方向的加速度时域曲线，如图3、5、7所示，其中采样频率为50 Hz。

由X、Y、Z3个方向的时域曲线可知，在旋翼转速上升初始阶段四旋翼飞行器姿态保持稳定，当四旋翼飞行器工作在一阶固有频率附近时，X、Y、Z方向的振动范围均超过±2 m/s2，四旋翼飞行器发生共振现象。

傅里叶变换能够准确辨识出信号的谐振情况，因此对共振时间内X、Y、Z 3个方向的加速度时域信号进行FFT频谱分析，结果如图4、6、8所示，可以看出图中主频均在10 Hz左右，对应四旋翼飞行器的一阶固有频率，次频均为23 Hz左右，对应四旋翼飞行器的二阶固有频率。实验结果与本文表3理论计算的结果基本一致，证明本文所用的多体系统传递矩阵法在四旋翼飞行器振动建模方面具有较好的精度。

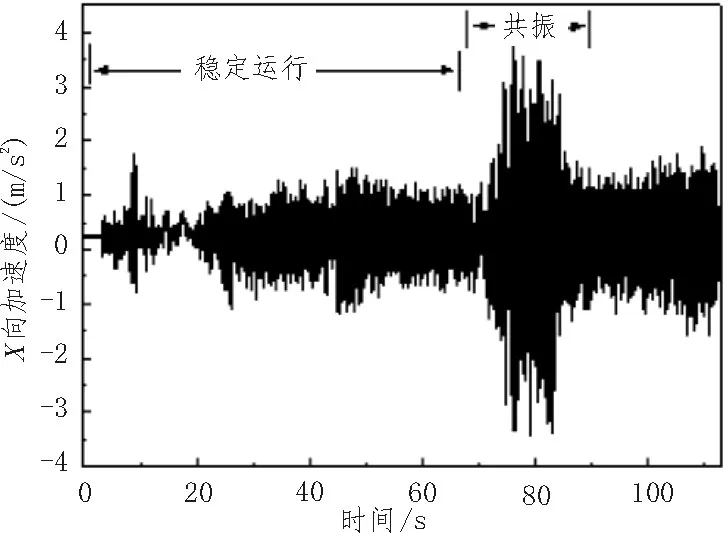
图3 X方向振动时域曲线

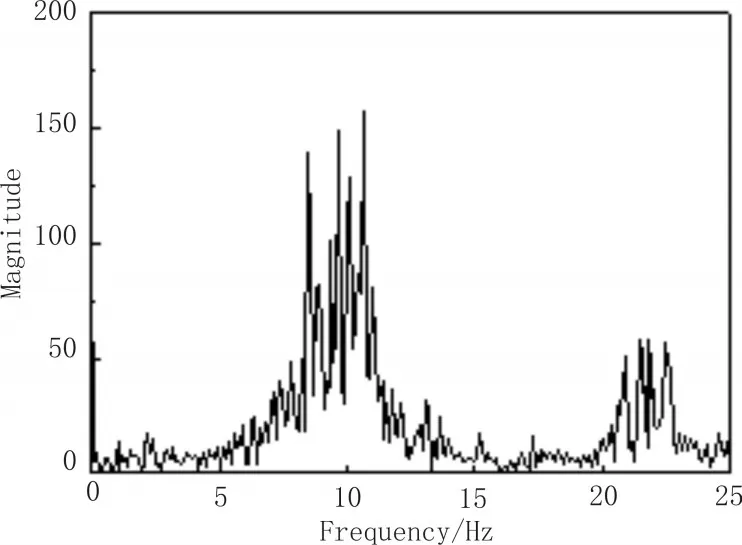
图4 X方向75～85s共振频域曲线

3 四旋翼飞行器模型修正

在研究四旋翼飞行器的控制问题中，文献[15]给出了一类常见的建模方法，根据牛顿-欧拉方程得出飞行器机体的非线性动力学模型之后，通过引入4个控制量，如式（21）所示，将复杂的非线性耦合系统解耦为4个独立的控制通道，在悬停状态下根据小扰动线性化原理将非线性模型进行线性化处理，从而得到每个通道的线性化模型。

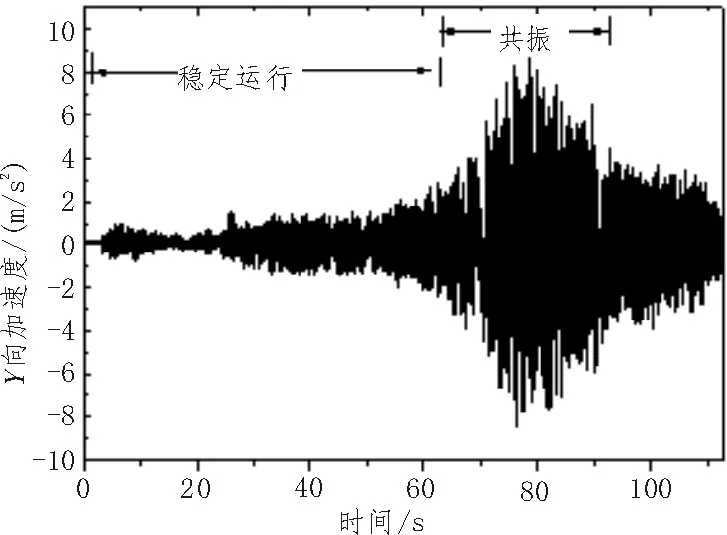
图5 Y方向振动时域曲线

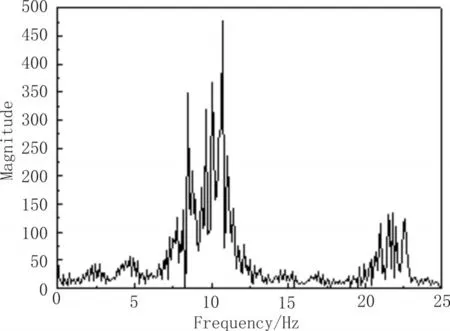
图6 Y方向75～85s共振频域曲线

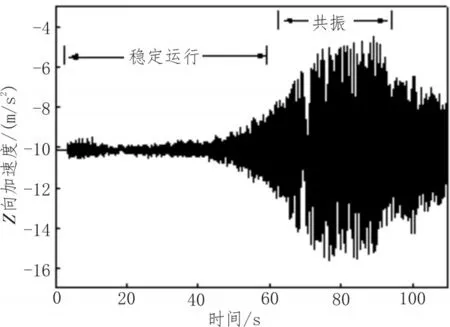
图7 Z方向振动时域曲线

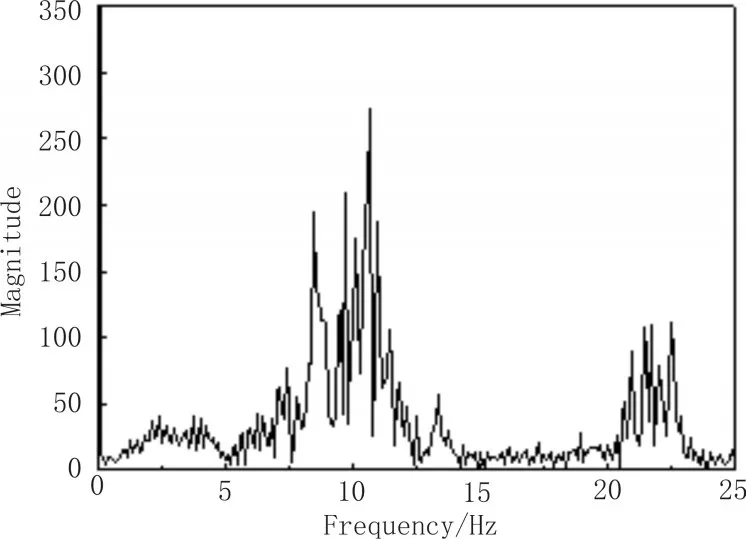
图8 Z方向75～85s共振频域曲线

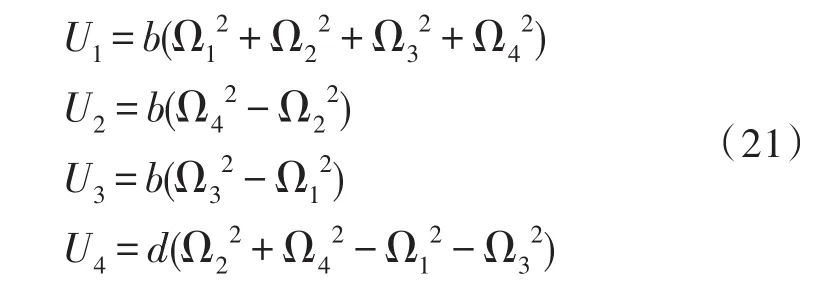
其中b为升力系数，d为反扭矩系数，Ωi为第i个旋翼的转速。

根据文献[15]的小扰动线性化理论以及本文中实际的四旋翼飞行器参数，俯仰通道开环传递函数可以表示为:

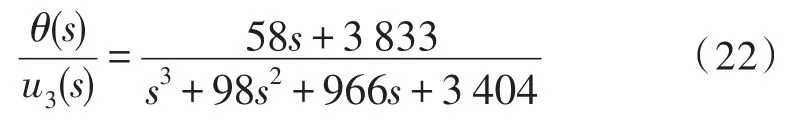
实际系统中，四旋翼机架的柔性、连接件的弹性等非刚体因素引起的谐振效应不可忽略，然而式（22）表示的俯仰角传递函数模型未对系统的谐振模态进行建模。后续通过设计复杂的控制器来补偿这种建模误差，虽然反馈控制元件能够反馈系统的响应，但动力学模型的过度简化常常导致难以预测的运动规律和多余的系统高频行为，从而严重影响控制精度和速度，因此引入系统的谐振模态对此类模型进行修正非常有必要。由于实际系统中高阶模态较难激发，因此工程上主要考虑系统的一阶模态。结合表3得到的四旋翼系统的固有频率，通过引入谐振环节，修正式（22）的传递函数模型，修正后的俯仰通道开环传递函数表示如下:

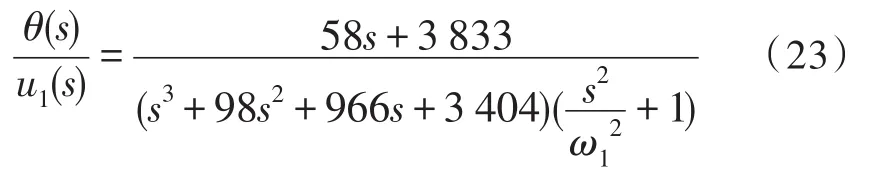
其中ω1为四旋翼系统的一阶固有频率，单位rad/s。

修正后的四旋翼动力学模型描述了系统的振动特性。图9实线部分表示修正后俯仰通道的开环频率特性，虚线表示加入PID控制器后系统的开环频率特性。对比发现在ω=ω1频率点附近系统增益均很大，即一阶模态被激发后系统可能出现较强的震荡，单纯通过经典的PID控制器难以对机械谐振抑制产生显著效果[16]，很难消除系统的震荡倾向，后续必须引入其他补偿措施滤除此谐振频率从而抑制共振[17]现象。

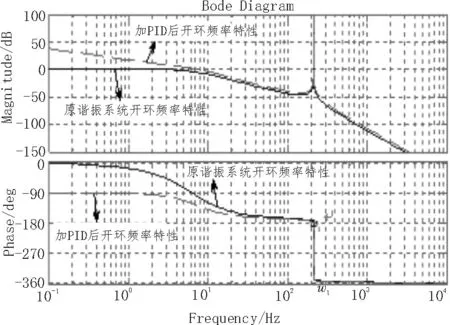
图9 修正后四旋翼俯仰通道的频率特性

4 结 论

文中针对四旋翼飞行器在飞行过程中的共振现象，以线性多体系统传递矩阵理论为基础，建立四旋翼系统的总传递矩阵模型，根据各元件的基本结构参数获得四旋翼飞行器的前十阶固有频率[18]，并通过实验验证了固有频率求解的准确性。在此基础上，修正了四旋翼飞行器未考虑系统谐振模态的常规动力学模型，提出了带有一个谐振峰的四旋翼飞行器模型。此模型不仅较为精确地刻画了四旋翼飞行器的振动特性，也为引入其他补偿措施抑制共振现象提供了理论基础，对四旋翼飞行器的建模和控制工作具有一定的指导意义。