基于DEMD的高压隔膜泵单向阀早期故障诊断
2018-08-25牟竹青黄国勇吴建德范玉刚
牟竹青, 黄国勇, 吴建德, 范玉刚
(1.昆明理工大学信息工程与自动化学院 昆明,650500) (2.云南省矿物管道输送工程技术研究中心 昆明,650500)
引 言
往复式高压隔膜泵是长距离、高浓度输送高温、高腐蚀固液两相介质的核心设备,其故障具有多源性、不确定性及并发性等特点,其工作运行状态是否正常直接影响到企业的生产效率。单向阀作为高压隔膜泵的核心机械零部件之一,易受输送矿物的粒径级配、浆体流变特性等因素的影响,比泵的其他部件更容易出现故障。为了预防单向阀由于磨损击穿等因素导致的工作故障,对单向阀的早期故障[1]诊断显得尤为重要。在单向阀故障早期诊断中,反映故障特征的冲击成分在整个振动信号中很微弱,且易受其他部件及环境的影响形成背景噪声,从而使单向阀的早期故障难以检测和诊断。
近年来,国内外学者以柴油机、离心泵、隔膜泵及压缩机等典型往复式机械设备为研究对象,开展故障机理及故障诊断方法的研究。目前,对往复泵单向阀的特性研究[2]较多,很少对其早期故障问题进行检测和诊断。早期故障诊断的方法大多数是通过时频域进行分析[3-4]。EMD是由Huang N E提出的一种有效的信号时频分析法,能够将非线性、非平稳的复杂振动信号自适应的分解成一系列IMF分量,并且具有一定的降噪能力,已被广泛应用到故障诊断中[5]。文献[6]利用考虑到EMD结合谱峭度法突出高频共振成分,从而检测出早期故障,但EMD的模态混叠现象对早期故障成分的提取存在影响。文献[7]利用DEMD和模糊熵结合的方法对轴承振动信号进行检测,虽然消除了模态混叠现象,但在进行分量信号筛选时运用相关系数法,有时不能准确提取出含有故障信号的分量信号。文献[8]利用EMD和包络谱分析相结合的方法对液压泵的早期故障特征进行了有效提取,并对故障类型进行了分类。
针对上述故障诊断方法的优缺点,笔者提出了基于DEMD的高压隔膜泵单向阀早期故障诊断方法。首先,对单向阀磨损击穿前的早期故障振动信号进行微分运算,使故障高频成分能量比增加,将微分后的信号进行EMD分解,将所得的IMF分量进行积分获得表征原始信号特征的有效分量;然后,计算分量信号与原信号的K-L散度值,将K-L散度值与所设阈值进行比较,剔除K-L散度小于阈值的虚假分量,将筛选出的分量信号进行重构;最后,利用Hilbert边际谱对重构信号进行瞬时频谱分析,以提取故障振动信号的特征。仿真与工程实验分析表明,该方法能够较好地提取出单向阀早期故障特征信息及特征频率。
1 高压隔膜泵及单向阀分析
1.1 高压隔膜泵及单向阀简述
以三缸单作用高压隔膜泵[9]为例,其工作原理为:电动机带动三拐曲轴、连杆和十字头运动,使旋转运动变为直线运动。当活塞左移时,利用油介质将隔膜室中隔膜吸到左方,借助压力打开进料单向阀,使矿浆充满隔膜室。当活塞右移时,利用油介质将隔膜室中隔膜推至右方,同时打开出料单向阀将矿浆排到泵外。
单向阀是控制进料和排料的方向性元件,使输送介质沿一个方向流动而不能倒流。根据隔膜泵工作原理,单向阀完成一次进料和排料的过程对应着隔膜泵的一次冲程。假设隔膜泵的冲程系数为50 r/min,其正常运行一天进出料单向阀需往复式动作72 000次。单向阀是运动最为频繁的部件,也是最易发生故障的部位。图1为高压隔膜泵的工作原理图及单向阀故障实物图。

图1 高压隔膜泵工作原理图及故障单向阀实物图Fig.1 Working principle diagram of high pressure diaphragm pump and check valve failure entity diagram
1.2 单向阀正常运行频率分析
笔者采用的实验数据来自云南大红山铁精矿长距离输送管道,其高压隔膜泵中的单向阀为锥式单向阀,锥式单向阀包括阀体、阀芯和弹簧。单向阀的阀芯和弹簧可看作是一个二阶振荡环节,受其内部结构限制的影响,频率[10]为
(1)
其中:ks为弹簧刚度;mv为阀芯弹簧系统的等效质量。
根据泵的柱塞运动情况,将弹簧刚度设为
ks=4π2(2f)2mv
(2)
其中:f为高压隔膜泵正常运行的频率。
弹簧-阀芯系统的频率fp=2f,根据实际情况,高压隔膜泵的正常运行频率为0.5~0.517 Hz,求得单向阀正常运行的频率fp为2(0.5~0.517)Hz,即1~1.034 Hz。当泵单向阀出现故障时,其特征频率为单向阀的固有频率和其倍频特征频率。
2 基于K-L散度的DEMD算法
2.1 DEMD算法及K-L散度
早期故障是指处于早期阶段的故障、弱故障或者潜在故障,其故障征兆不明显。若这类故障不能被检测并及时处理,将会引发严重的事故。早期故障特征表现不明显,特点为幅值小、变化缓慢,且变化的信息容易被系统中存在的各种干扰和噪声淹没[11]。其故障成分可看成高频冲击成分大多数情况下能量占比较低,从而提取的振动信号中故障冲击成分不明显,针对此种情况,有学者提出DEMD算法。DEMD算法首先是对信号进行微分运算,将微分后的信号进行EMD分解,然后将所得IMF分量进行积分运算获得能够表征原始信号的有效IMF分量。DEMD的具体分解步骤参考文献[12]。DEMD算法的基本原理如下。
1) 通过对原始信号先进行微分运算变换,微分变换对类似脉冲信号等突变信号非常敏感,能放大信号的局部波动特征且能改变信号的振幅比。以一个信号为例说明微分运算的作用,信号表达式为
x(t)=A1(sin2πf1t)+A2(sin2πf2t)
(3)
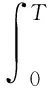
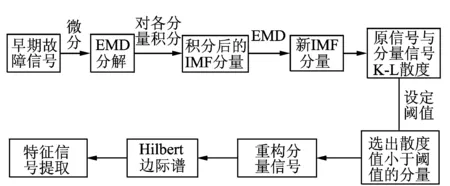
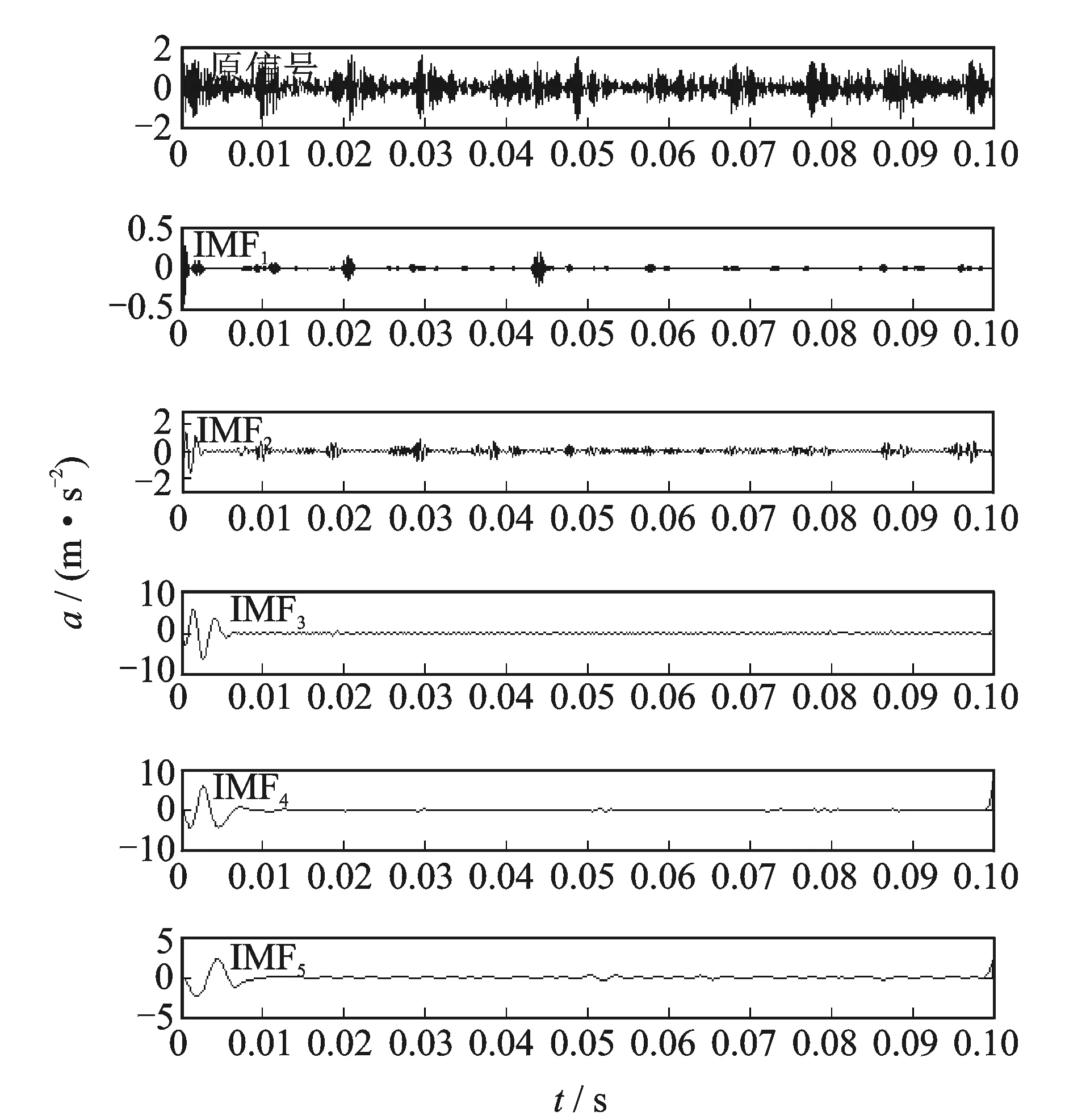
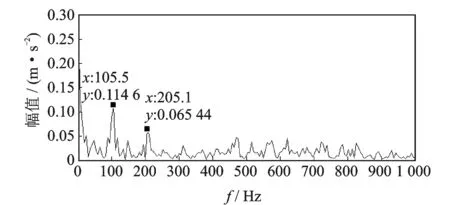
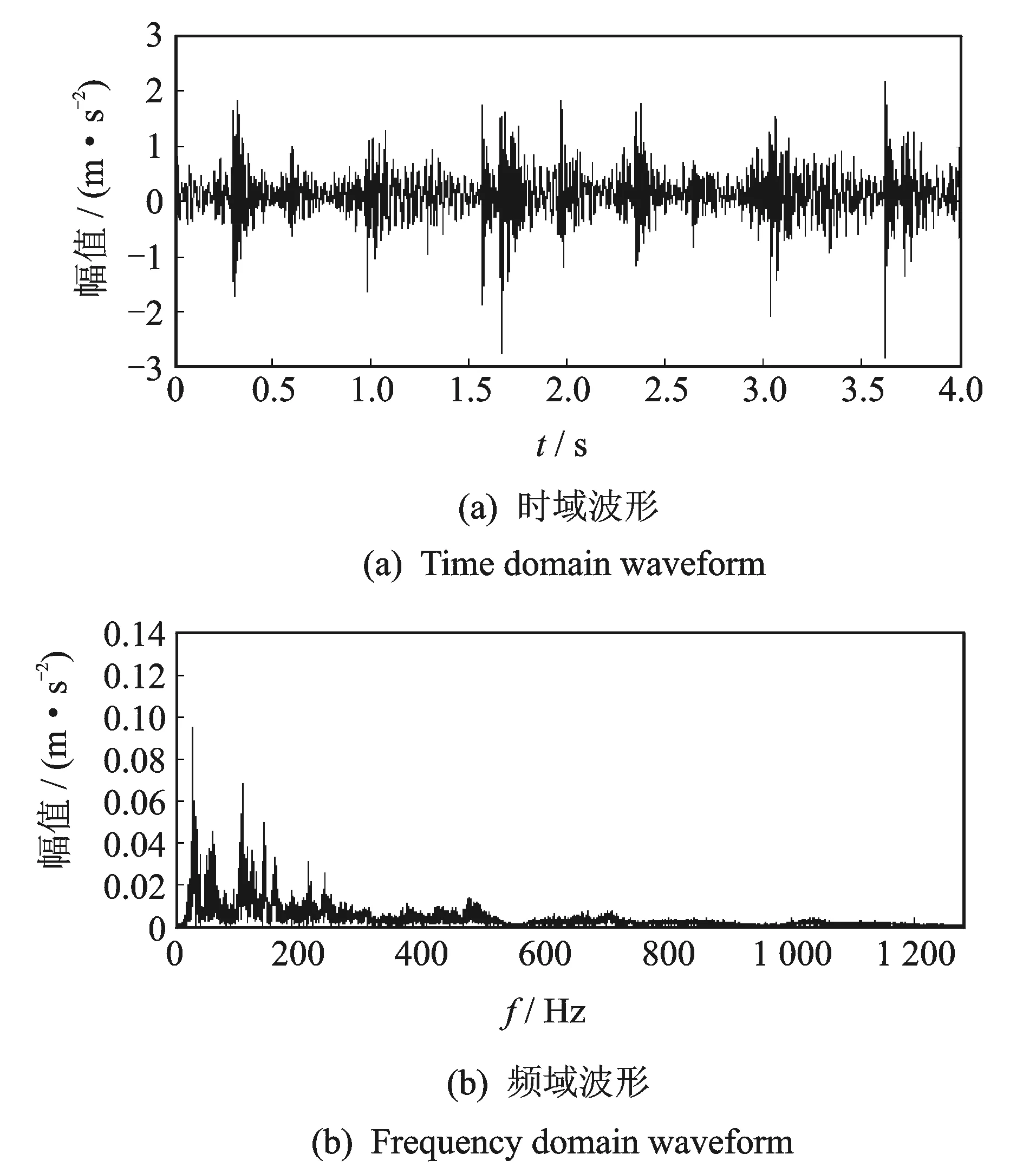
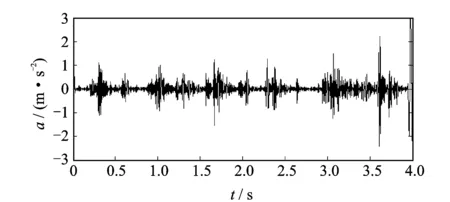
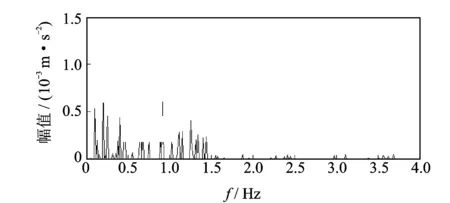
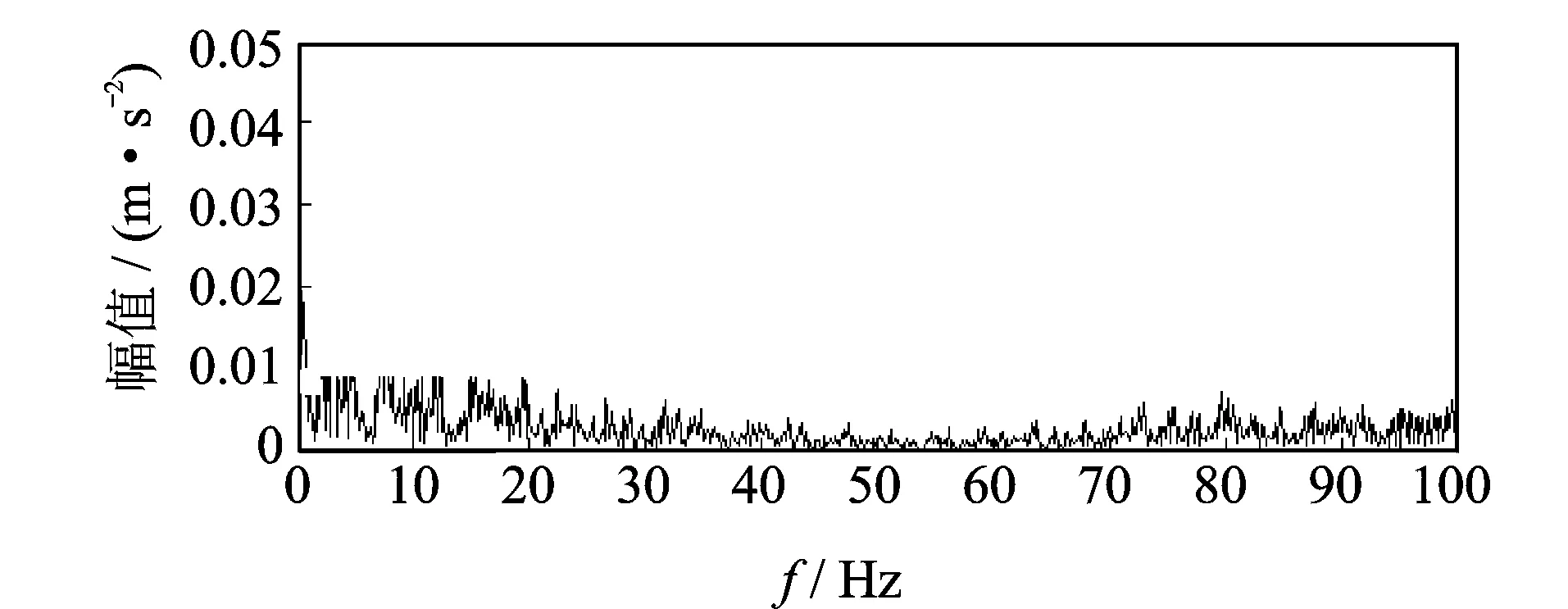
其中:A1,A2为信号幅值;f1,f2为信号频率,且f1>f2,A1 对x(t)进行微分运算,得到 x′(t)=2πf1A1cos(2πf1t)+2πf2A2cos(2πf2t) (4) 2) 对微分后的信号进行EMD分解,利用Hilbert变换解调[13]法判断经EMD分解后的分量信号中是否出现模态混叠现象。若存在模态混叠现象,则继续对信号进行微分及EMD分解,这样可以使振动信号中微弱或相近的频率成分分离开。 3) 将分解出的分量信号进行积分还原,再对积分后的信号进行一次EMD分解,可以消除积分运算造成的信号幅值的漂移,也可保证最后得到的分量信号为内在IMF分量。 单向阀早期故障振动信号经DEMD分解后得到一系列IMF分量,为了有效提取出单向阀早期故障信号中的故障信息较明显的IMF分量,必须运用一种较为准确的IMF分量选择算法。目前,相关系数法[14]在提取分量信息领域中应用比较广泛,但有时求出的各分量的相关系数较为接近,导致不能准确提取出主要的分量信号。因此,笔者提出一种基于K-L散度的DEMD分量选择算法。 K-L散度[15]也称为方向散度或Kullback-Leibler距离,是信息论中的一个重要概念。设p1(x)和p2(x)为连续随机变量X的两个过程的概率,定义K-L距离为 (5) p1(x)和p2(x)二者的K-L散度为 D(p1,p2)=δ(p1,p2)+δ(p2,p1) (6) 以笔者使用的单向阀早期故障振动信号为例,简单阐述K-L散度选取IMF主分量的步骤。 1) 假设早期故障振动信号X=x1,x2,,xn和某一经DEMD算法分解后的分量信号Y=y1,y2,,yn,用非参数密度估计法计算两个信号的概率分布, 分别用p1(x)和p2(x)表示为 (7) 其中:p1(x)为信号X的核密度估计;K(·)成为核函数;h为给定的正数,称为窗宽或平滑参数。 2) 将两个信号的概率分布带入式(5)求出K-L距离,信号X的K-L距离为δ(p1,p2),信号Y的K-L距离为δ(p2,p1)。 3) 将两个信号的K-L距离带入式(6),计算出二者之间的K-L散度值。 4) 对求得的K-L散度值进行归一化处理。 5) 设定一个适当的阈值d,所求的K-L散度值小于该阈值的分量为含有故障信特征信息明显的主分量。不同情况下,阈值d的取值不尽相同。根据本研究所取数据,设定阈值为0.01。 根据上述分析,DEMD算法可提高振动信号中高低频分量的振幅比,增强了EMD的频带分解能力,有利于提取微弱高频成分。在DEMD分解的基础上,利用K-L散度表征原故障振动信号与IMF分量信号的相关程度,选取与原故障振动信号的K-L散度值小的IMF分量进行后续的分析。 将选取的有效IMF分量进行Hilbert变换,得到瞬时频率,即 (8) 构造解析信号 s(t)=ci(t)+iHci(t)=ai(t)ejφi(t) (9) 得到瞬时幅值函数和相位函数分别为 进而求得瞬时频率为 ωi(t)=dφi(t)/dt (11) 则 (12) 在此省略了残余函数rn(t),定义边际谱[16]为 (13) 其中:T为振动信号的总长度。 Hilbert边际谱属于频域特性曲线,能真实反映频率的存在及信号幅值在整个频率段上随频率变化的情况,能较好地提取故障特征。 笔者提出了基于DEMD的高压隔膜泵单向阀早期故障诊断方法,具体步骤如下。 1) 选取10 240组单进料单向阀击穿前的早期故障数据进行工程实验验证。 2) 对选取的单向阀早期故障数据进行微分运算,微分后的信号频率不会发生改变,但可提高振动信号中高低频分量的振幅比,增强了EMD的频带分解能力,有利于提取微弱高频成分。 3) 对微分后的数据进行EMD分解,将分解后的IMF分量信号进行积分运算还原,再对积分后的信号进行一次EMD分解,获得表征原始信号特征的内在IMF分量。 4) 计算原始信号与步骤3中得到的各个IMF分量进行K-L散度计算,将得出的K-L散度值进行归一化处理。 5) 设定一个阈值,将归一化后的K-L散度值与设定的阈值进行比较,找出小于阈值的IMF分量信号,散度值越小,证明IMF分量信号与原信号的相关程度越高。 6) 根据K-L散度选出的分量信号进行重构,重构后的信号利用Hilbert边际谱进行瞬时频谱分析,提取故障特征信息。 基于上述步骤,笔者提出的方法能够较好提取单向阀早期故障特征信息及特征频率,该方法的流程如图2所示。 图2 基于DEMD的高压隔膜泵单向阀早期故障诊断方法流程Fig.2 DEMD based early fault diagnosis method for high-pressure diaphragm pump check valve 为了验证此方法在早期故障诊断中对特征信息提取的有效性,笔者进行仿真分析,选取的仿真信号为美国凯斯西储大学电气工程实验室的轴承外圈早期故障数据。采用的轴承型号为6205-2RS JEM SKF,采样频率为48 kHz,数据长度为4 800,在轴承外圈上加工直径为0.177 8 mm、深度为0.279 4 mm的小槽来模拟早期故障信号。根据轴承振动理论,计算得到轴承外圈故障基频f1=103.36 Hz。 首先,取4 800组模拟的外圈早期故障数据对外圈故障信号进行进行DEMD分解,分解成若干个IMF分量。图3为外圈故障原信号及分解的前5个分量信号。计算这5个分量信号与原信号的K-L散度及相关系数,通过计算相关系数既可以辅助选择分量信号,也能验证K-L散度对分量信号选择的有效性。分量信号的K-L散度及相关系数图如表1所示。通过表1可以看出:IMF1和IMF2的K-L散度值很小,小于所设阈值,证明其与原信号的相关程度较大,能凸显出原信号的信号特征;IMF3,IMF4和IMF5的K-L散度大于所设阈值,故其分量为无用的虚假分量。从相关系数也可看出,IMF1,IMF2和IMF3的相关系数都较大,但区别没有K-L散度值明显,很难判断出真实的分量信号,故K-L散度较相关系数能更好地进行分量信号的选择。 图3 外圈故障原信号及DEMD分解结果Fig.3 Outer ring fault signal and DEMD decomposition results Tab.1K-Ldivergenceandcorrelationcoefficientoftheouterringfaultsignalandthesignalofeachcomponent 参数IMF1IMF2IMF3IMF4IMF5K-L散度0.002 00.001 80.086 30.389 4 0.621 2相关系数0.224 80.318 70.112 20.014 1-0.011 0 根据K-L散度所筛选的IMF1和IMF2分量进行信号重构,如图4所示。对重构信号利用Hilbert边际谱进行分析,如图5所示。图5可清晰定位到接近于外圈故障的基频值104.4 Hz,并能有效定位到9倍频,因此可准确判别出轴承外圈故障状态。作为对比,将本研究方法与文献[14]中采用EEMD和相关系数的方法进行对比,文献[14]外圈特征提取结果如图6所示。可以看出,虽然能提取到外圈故障的基频,但高频处没有明显的故障特征频率。 图4 外圈故障重构信号Fig.4 Fault reconstruction signal of outer ring 图5 重构信号的Hilbert边际谱Fig.5 Hilbert marginal spectrum of reconstructed signal 图6 文献[14]外圈特征提取结果Fig.6 The results of the outer ring feature extraction in reference[14] 本实验数据来源于云南大红山管道三号高压隔膜泵站,该泵站的高压隔膜泵型号为TZPM系列的三缸曲轴驱动活塞式隔膜泵,最高工作压力为24.44 MPa。分别对同一泵组三对进料单向阀和出料单向阀布置型号为PCB-ICP的振动加速度传感器,加速度传感器的另一端连接振动信号采集系统,采集卡采用型号为PXIe-3342高精度8通道动态数据采集卡,通过与电脑相连实时监测单向阀运行情况。由于单向阀均为进料阀和排料阀成对匹配工作,因此随机选择某组进、排料单向阀振动数据进行实验分析。笔者采用的数据为单向阀早期磨损故障运行状态的振动信号,通过考虑采样频率对隔膜泵压力的影响,该数据的采样频率设为2 560 Hz,采样数据长度为10 240。 图7 单向阀故障运行的时域波形和频域波形图Fig.7 Time domain waveform and frequency domain waveform of faulty operation of check valve 图8 单向阀故障运行信号的DEMD分解结果Fig.8 DEMD decomposition result of fault operation signal of check valve 图9 单向阀故障重构信号Fig.9 Fault reconstruction signal of check valve 取10 240组单向阀早期故障运行数据,图7为其时域波形和频域波形。可以看出,早期故障运行时频率主要集中在0~200 Hz,不能判断出是否发生故障。为了进一步分析单向阀故障时的主导运行频率,故对故障振动信号进行DEMD分解,分解成若干个IMF分量。图8为单向阀早期故障振动信号及分解的前5个分量信号。计算这5个分量信号与原信号的K-L散度及相关系数,通过表2可看出,IMF3和IMF4的K-L散度值很小,小于所设阈值,证明它们与原信号的相关程度较大,更能凸显出原信号的信号特征;而IMF1,IMF2和IMF5的K-L散度大于所设阈值,故这几个分量为无用的虚假分量。从相关系数也可以看出,IMF2,IMF3和IMF4的相关系数都较大,但区别没有K-L散度值明显。 图10 单向阀故障重构信号的Hilbert边际谱Fig.10 Hilbert marginal spectrum of fault reconstruction signal of check valve Tab.2K-Ldivergenceandcorrelationcoefficientofthefaultoperationsignalofcheckvalvelandthesignalofeachcomponent 参数IMF1IMF2IMF3IMF4IMF5K-L散度0.172 70.044 10.001 60.001 00.189 5相关系数0.027 00.141 40.332 30.247 80.115 6 根据K-L散度筛选出的IMF3和IMF4分量进行信号重构,重构信号如图9所示。对重构信号利用Hilbert边际谱分析,如图10所示。从图10可知,获得了与单向阀正常运行基频1~1.034 Hz相近的频率成分1 Hz及其2倍频和4倍频成分,且成为信号的主导频率成分,由此可知单向阀必定发生了故障。将本研究方法与文献[14]中采用EEMD和相关系数的方法进行对比,文献[14]单向阀早期故障提取结果如图11所示。可以看出,此方法能提取到单向阀早期故障的基频及三倍频,但效果没有本研究方法好,故本研究方法更易提取出单向阀早期故障特征信息。 图11 文献[14]单向阀故障提取结果Fig.11 The results of the fault signal of check valve in reference[14] 1) 对原故障信号在EMD分解的基础上进行微积运算,能够提高振动信号中高低频分量的振幅比,增强了EMD的频带分解能力,从而增加了故障高频成分的比重,有利于提取微弱高频成分。 2) 计算原信号与各IMF分量信号的K-L散度值,选取K-L散度值小于所设阈值的IMF分量信号作为有效分量信号,能够避免相关系数法对选取分量时的不准确性。 3) 对选取的分量信号进行重构,并利用Hilbert边际谱对重构信号进行瞬时频谱分析,以提取故障特征信息。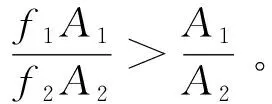
2.2 基于K-L散度的IMF分量选择算法
3 Hilbert边际谱
4 基于DEMD的高压隔膜泵单向阀早期故障诊断方法
5 仿真分析



6 工程实验验证


7 结 论
