基于稀疏分解的轴承声阵列信号特征提取

郭莹莹， 赵学智， 上官文斌， 张春良

(1.华南理工大学机械与汽车工程学院 广州，510641) (2.广州大学机械与电气工程学院 广州，510006)

引 言

滚动轴承是机械设备中最重要的部件之一，其状态的好坏直接关系到设备的正常运转，因此对滚动轴承的状态监测和故障诊断一直是非常重要的研究课题[1]。利用振动传感器检测轴承振动，并通过对振动信号的特征提取来识别轴承的故障状况是一种应用最为广泛的方法，其中的特征提取方法主要有小波及小波包分析[2-3]、经验模式分解[4]、稀疏分解[5-6]、独立分量分析[7]、谱峭度[8]和形态滤波[9]等方法。

虽然基于振动传感器的轴承故障诊断技术取得了广泛应用，但是在高温、高腐蚀及运动等难于接近的场合下，安置振动传感器非常困难，此时不适于采用振动传感器来监测轴承的运动状态。由于传声器可以在较远距离采集到声音信息，且声音是振动产生的，其频率为振动频率，因此在这些难于接近的场合下采用传声器来检测轴承的振动是一种不错的选择。鉴于传声器的非接触、可实现较远距离检测等特点，研究人员已经较早开展了声学故障诊断研究。美国铁道协会及所属研究机构开发出了一套轴承道旁声学监测系统，采取传声器对列车轴承的运动状态进行监测[10]。Deblauwe[11]和Hald[12]基于发动机噪声完成了制动器噪声源分析、发动机的撞击启动及撞击噪声分析。Lu等[13]将近场声全息和灰度共生矩阵结合用于轴承故障诊断等。这些研究都证明了利用声信号进行故障诊断是可行的。

利用声信号对轴承进行状态监测和故障诊断遇到的最大问题是噪声干扰。现场采集到的轴承故障声信号信噪比差，成分复杂，在介质中会迅速衰减。针对这一问题，研究者们采用了不同的方法来解决。Routray等[14]用小波方法和盲源分离的方法消除噪声。Amarnath等[15]用经验模态分解(empirical mode decomposition，简称EMD)方法处理滚动轴承故障的声信号，提取振动特征。周俊等[16]将时域盲解卷积、形态滤波和频域压缩感知重构的稀疏分量分析相结合应用于轴承复合故障声学诊断。这些方法对消除轴承声信号中的噪声都取得了较好的效果。

笔者结合全息技术与稀疏分解算法的优点，提出一种基于稀疏分解的轴承声阵列信号特征提取方法。首先，利用近场声全息声源识别技术判断机械设备的主要噪声源；然后，根据轴承故障声信号的频率特征和冗余字典的稀疏特性建立由coif4小波字典和局部余弦字典组成的冗余字典来稀疏逼近原信号，并采用拉格朗日基追踪算法去噪。对于基追踪的基不稳定问题，利用拉格朗日基追踪方法直接求解稀疏去噪会更有效[17]。与以往方法相比[14-16]，本研究方法没有EMD方法存在的模态混淆和端点效应，而文献[14]中的盲源分离处理实际非线性信号的能力欠佳，且本稀疏分解算法中的基追踪所挑选的向量为线性无关，比匹配追踪(贪婪算法)更适用于分解含有相近时频结构的信号。笔者对模拟的含噪轴承声信号进行了分析，搭建了轴承声阵列信号故障诊断实验平台。利用两种传声器阵列识别设备主要噪声源后再对“热点”所对应信号进行稀疏分解，提取清晰的故障特征频率，准确识别了轴承故障。

1 轴承振动的近场声全息声源识别原理

近场声全息声源识别技术的最大特点是由传声器阵列信号采集设备在近场区域记录被测对象发出的声波，再用分析处理算法对声源的辐射声压直接进行分析成像或重建，其中传声器测量面为全息面。在自由与半自由声场中，由点声源声压级关系可知，每当测量距离增大一倍，声压级就会减少6dB，且当全息面距离声源大于一个波长时，传声器只能采集到声源的宏观信息(传播波)而丢失了声源的细节信息(倏逝波，其幅值随距离的增加而指数衰减)。根据波速(v=340m/s)等于波长λ与频率f的乘积，当轴承故障特征频率在f=20～500Hz范围内时，声波长λ=0.68～17m。因此，可以采用传声器阵列在近场(测量距离小于声波波长d≪λ)区域记录并显示轴承的全息数据。

轴承元件受迫振动时辐射的声波随时间和空间快速改变，利用全息面有效声压场可以获得声源个数、位置及强度等信息，并通过对比正常与故障轴承工况下的设备声压图，识别出主要噪声源位置，进而判断关键部位轴承是否异常。

2 稀疏分解原理

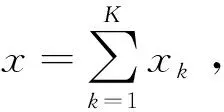
(1)

其中：D为信号空间RN中的过完备冗余字典，D=D1,D2,,Dk；αk为对应于每个字典的分解表示系数。

2.1 拉格朗日基追踪算法

在冗余字典中，利用基追踪算法选取多个字典向量计算信号的最优逼近使误差最小，这是一个非确定性多项式难题(non-deterministic polynomial-hard,简称NP-hard问题)，所以未必得到最优的逼近。式(1)的解可通过极小化l0拉格朗日函数获得。l0伪范数是非凸的，此极小化问题难以求解，且当字典个数增加时计算将更加复杂。因此，为了逼近信号x，将关于分解系数αk的l0范数优化求解问题归结为式(2)中ak的l1范数优化问题

(2)

式(2)为凸函数，通过其拉格朗日追踪的松弛公式求解

(3)

其中：T为拉格朗日乘子，即阈值。

对于信号xk，可得

(4)

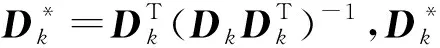
由式(3)，(4)可知，式(2)中计算系数{a1,,ak}可转换为计算{x1,,xk}的问题

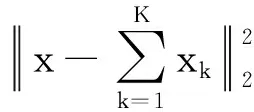
(5)

式(5)中{x1,,xk}的求解算法步骤为：

1) 选合适的字典Dk构造冗余字典D；

2) 设定阈值T，初始化迭代次数n；

3) 初始化各信号xk=0；

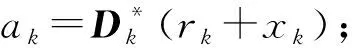
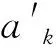
2.2 冗余字典的构建

图1为在半消声实验室内采集的轴承内圈(SKF6205-2RSJEM，裂纹尺寸约为0.1 mm×15 mm×0.28mm，转速为1 800r/min)故障声信号的时域波形图，其故障冲击间隔理论值为0.006 2s。图中的故障声信号包含冲击信号、谐振信号和噪声，故不宜选用单一的小字典稀疏表示，需选择能稀疏表示各有效信号的字典来构建冗余字典(Dk的个数大于k)。

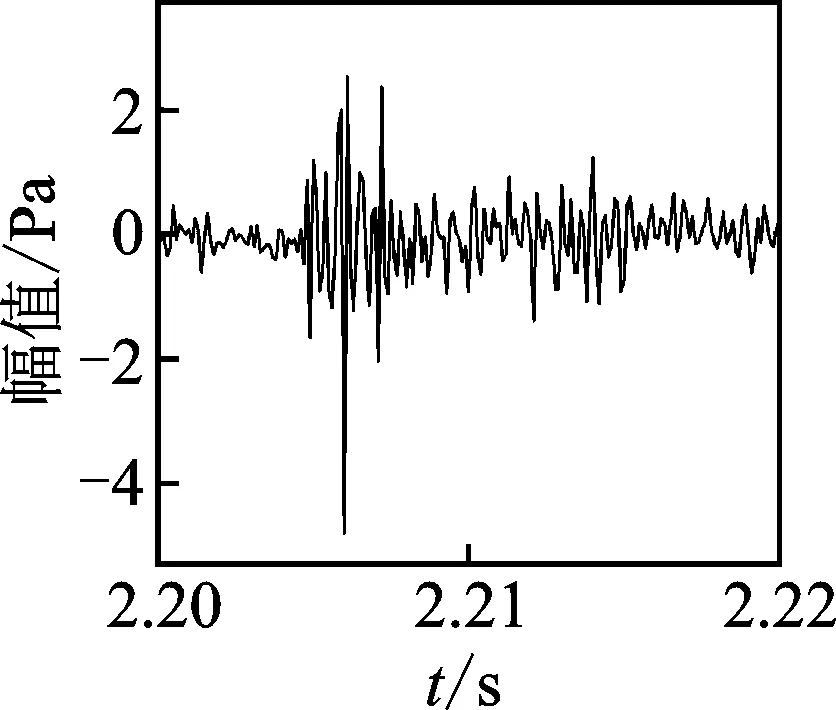
图1 轴承内圈故障声信号的时域波形图Fig.1 Acoustic signal time-domain waveform of bearing inner ring fault

常用的冗余字典有Dirac字典、Fourier字典、小波字典和局部余弦字典等。一组最优基是一组与信号时频结构匹配最好的时频铺叠。根据图1信号特点，为了减少稀疏分解中最佳基逼近的复杂度，可选择时频标准正交字典，如小波字典和局部余弦字典。

小波字典由一个积分为零的母小波Ψ构造，通过伸缩函数的尺度参数s和平移时域u后可得

(6)

由式(6)可知，小波字典将频率轴分成不同长度的区间，能为奇异点提供更稀疏的表示，适合逼近图1中的冲击信号。

常用的小波函数有Haar小波、Daubechies小波、Meyer小波、symN小波族(变量N表示小波函数的消失矩阶数，一般N=2，3，)和coifN小波族等。小波字典与信号的相似性越高，字典的稀疏性越好，因冲击信号具有快速衰减的特点，需选择具有指数性和正交性(便于重构)，且存在紧支集的小波基函数。其中，sym8小波和coif4小波为正交小波，具有较长的支集长度和较大的消失矩，且对称性较好，重构时不易失真。sym8小波消失矩比coif4小波的大，信号分解后高频分量更少，低频分量更多，使运算量增加，冲击信号峰值被削弱的更多。因此，coif4小波字典更适宜匹配轴承故障声信号，其尺度函数和小波函数如图2所示。

图2 Coif4小波的尺度函数和小波函数Fig.2 Scaling function and wavelet function of coif4

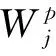
(7)

由式(7)可知，局部余弦字典将时间轴分成不同长度的区间，且Heisenberg时频盒沿频率平移，其时频分辨率与谐波结构相适应，适合逼近谐振信号。

综上所述，通过分析轴承内圈故障声信号时频特征和冗余字典稀疏特性，选用coif4小波字典和局部余弦字典构建冗余字典。

3 仿真分析

利用模拟的声信号验证本研究方法可以在复杂的噪声背景下有效提取轴承声信号的故障特征。以内圈故障声信号为例，其模型为

x(t)=r(t)+s(t)+h(t)

(8)

其中：x(t)为复合声信号；r(t)为噪声信号；s(t)为冲击信号；h(t)为谐振信号。

u(t-mT)exp-β(t-mT)

(9)

其中：s(t)由M个幅值为B、衰减系数为β、高频共振频率为fn的冲击成分组成；T为冲击间隔；f=1/T为冲击故障频率；u(t)为单位阶跃函数；fr为转频。

(10)

其中：h(t)由K个幅值为A、频率为fi的谐波构成。

为了使仿真更接近实际，取采样频率fs=10kHz，采样点数N=99 000，加入高斯白噪声, 使信噪比SNR=-15，并将表1中的参数代入式(8)～(10)，得到仿真合成声信号时域图及Hilbert包络频谱图，如图3所示。可以看出，冲击特征已被强噪声完全淹没，普通的Hilbert包络解调方法无法提取仿真信号的冲击故障特征。

利用本研究方法对图3所示的仿真合成信号进行稀疏分解并包络解调，提取到的冲击信号及其Hilbert频谱图如图4所示。可以看出，噪声已基本被分离，时域图中有明显的周期性冲击特征，其Hilbert频谱图中转频31.3Hz及二倍转频60.1Hz、内圈故障特征频率164.1Hz及其2～5次谐波和边频处峰值(接近理论值)比较凸显。仿真实例证明，本研究方法可在复杂的噪声背景下准确提取故障特征。

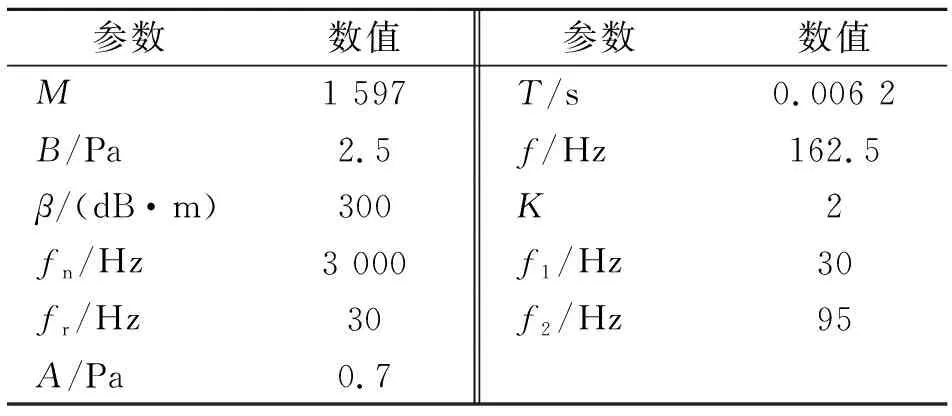
表1 仿真信号各参数值

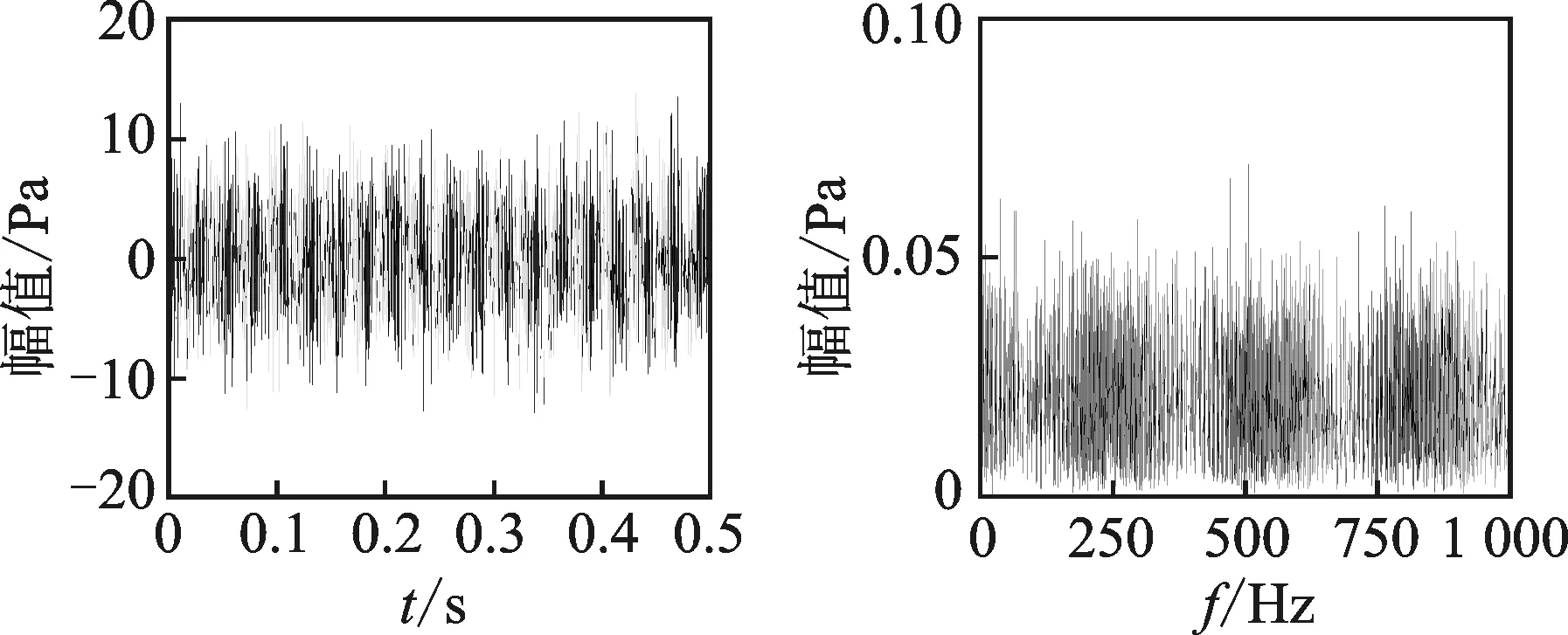
图3 仿真合成声信号时域图及Hilbert频谱图Fig.3 Time-domain diagram and Hilbert spectrum of acoustic synthetic signal

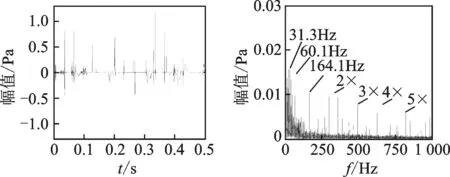
图4 稀疏分解提取到的冲击信号及Hilbert频谱图Fig.4 Impact signal extracted by sparse decomposition and its Hilbert spectrum

4 实例分析

4.1 实验平台

为了验证基于稀疏分解的轴承声阵列信号特征提取方法的有效性，在实验室内搭建轴承声阵列信号故障诊断实验平台。平台四周堆叠高为2m的吸声尖劈形成简易半消声室，实验数据在凌晨0～6点采集，环境噪声较小。如图5所示，该平台主要由轴承实验台、传声器阵列以及声频信号采集处理系统组成。图5(a)所示，工作原理为：a.利用数据采集箱(PXI1033)和采集卡(Express Card-8306)采集MP201电容型传声器(直径为0.012 7m，频率响应范围为6.3～20kHz)阵列测得的本特利RK4轴承实验台声信号数据；b.对比分析传声器阵列全息面三维有效声压场图，根据“热点”判断关键部位轴承工作状态是否异常；c.利用上述特征提取方法对“热点”声信号进行故障特征提取，进而判断故障类型。

图5(c)和(d)中，传声器阵列架为7×7平面网格(0.1m×0.1m)结构，置于轴承实验台正前方(阵列传声器端面与转轴轴心线的垂直距离为18.2cm)。考虑到轴承实验台为长方形结构，可适当减少纵向传声器个数。因此，实验拟采用6×6和4×6两种传声器阵列。其中，6×6和4×6阵列中的第4和第19通道传声器正对轴承实验台的电机，而第22和第7通道正对实验轴承所在轴承座。

图5 轴承声阵列信号故障诊断实验平台Fig.5 Microphone array signal fault diagnosis experiment platform of bearing

轴承处于空载状态，转速分别取1 800r/min和1 500r/min。图6为线切割加工的外圈和内圈裂纹故障。根据表2中的轴承结构参数，计算出外圈和内圈的故障频率分别为3.584 8fr和5.415 2fr(fr为转频)。当轴承转速为1 800r/min(fr=30Hz)时，外圈和内圈的故障频率理论值分别为107.54Hz和162.46Hz。当转速为1 500r/min(fr=25Hz)时，外圈和内圈的故障频率理论值分别为89.62和135.38Hz。

图6 故障轴承Fig.6 Failure bearings

参数数值外径/mm52内径/mm25宽度/mm15滚动体接触角α/(°)0外圈裂纹宽度1/mm0.5内圈裂纹宽度1/mm0.5内圈裂纹宽度2/mm0.1裂纹深度/mm0.28裂纹位置滚道宽度方向

4.2 实验结果及分析

实验中，信号采样频率为10kHz，每个通道数据长度为98 304。图7为传声器阵列采集的正常、内圈和外圈裂纹(0.1或0.5mm)故障轴承在不同转速下的全息面有效声压场及投影图。其中，图7(a)～(e)采用6×6传声器阵列，图7(f)和(g)采用4×6传声器阵列。经对比分析可知

1) 图7(a)中，只有电机附近的坐标(-0.2,0)有“热点”，且正常轴承有效声压低于故障轴承。

2) 图7(b)和(c)中的“热点”均出现在坐标(0,0)附近，即靠近轴承实验台中心位置，且实验轴承端声压较高。这是因为外圈裂纹引起的异常振动通过轴承座和轴传递，其产生的声音与电机噪声叠加而形成此热点。

3) 图7(d)中存在两个“热点”，一个在坐标(0,-0.1)处，其分布和成因与图7(b)的基本一致；另一个在坐标(0.1,0.1)处，即对应故障轴承，其声压略低于第1个“热点”。原因是电机和故障轴承均为噪声源，而第2个“热点”主要受故障轴承的影响。类似的，图(e)中也存在两个“热点”，其性质与图7(d)中的相同。

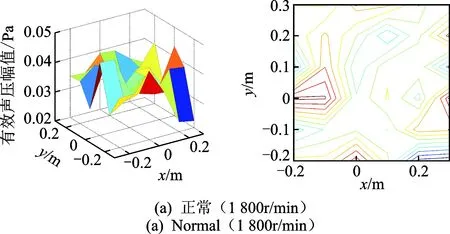
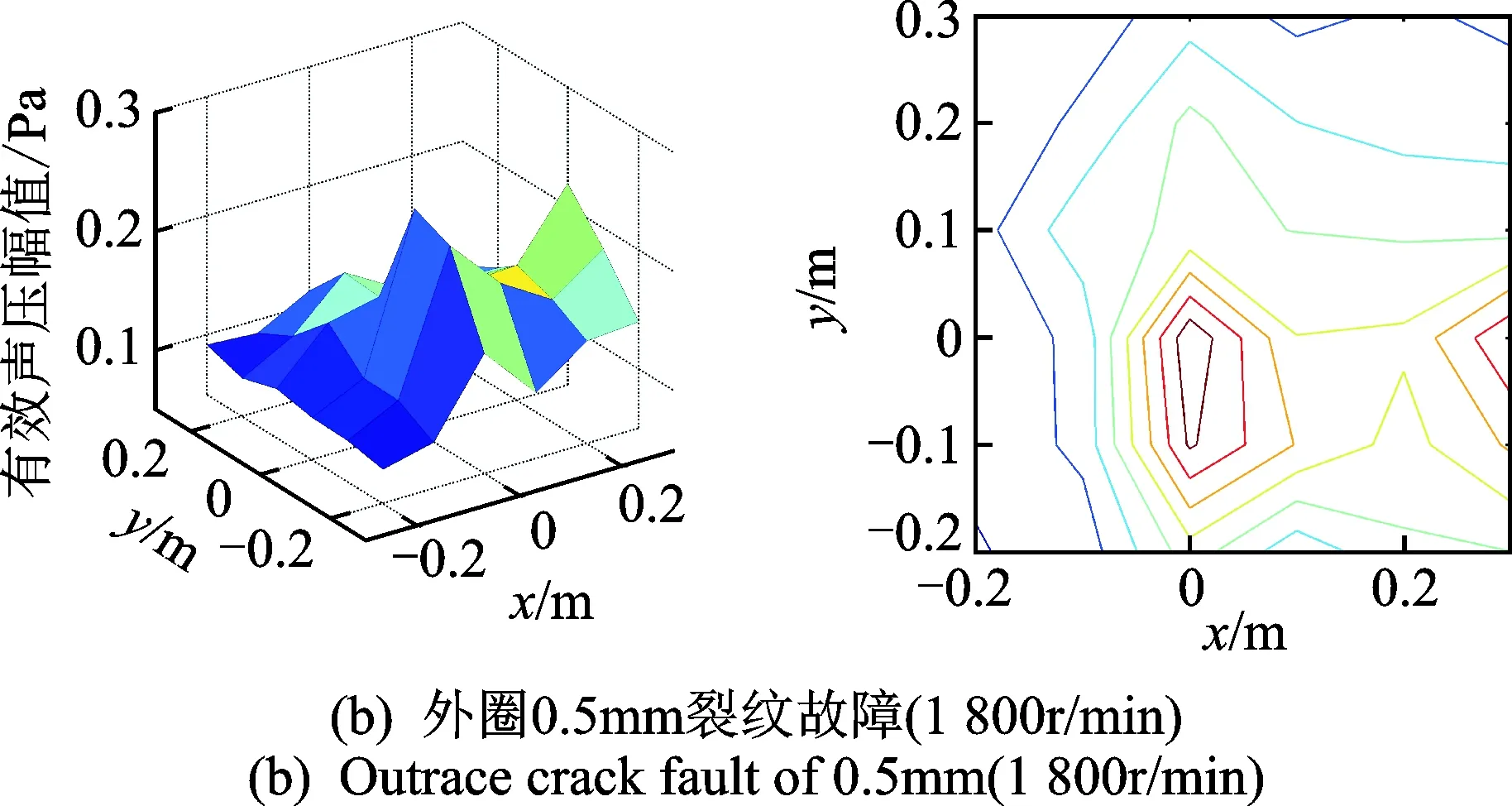
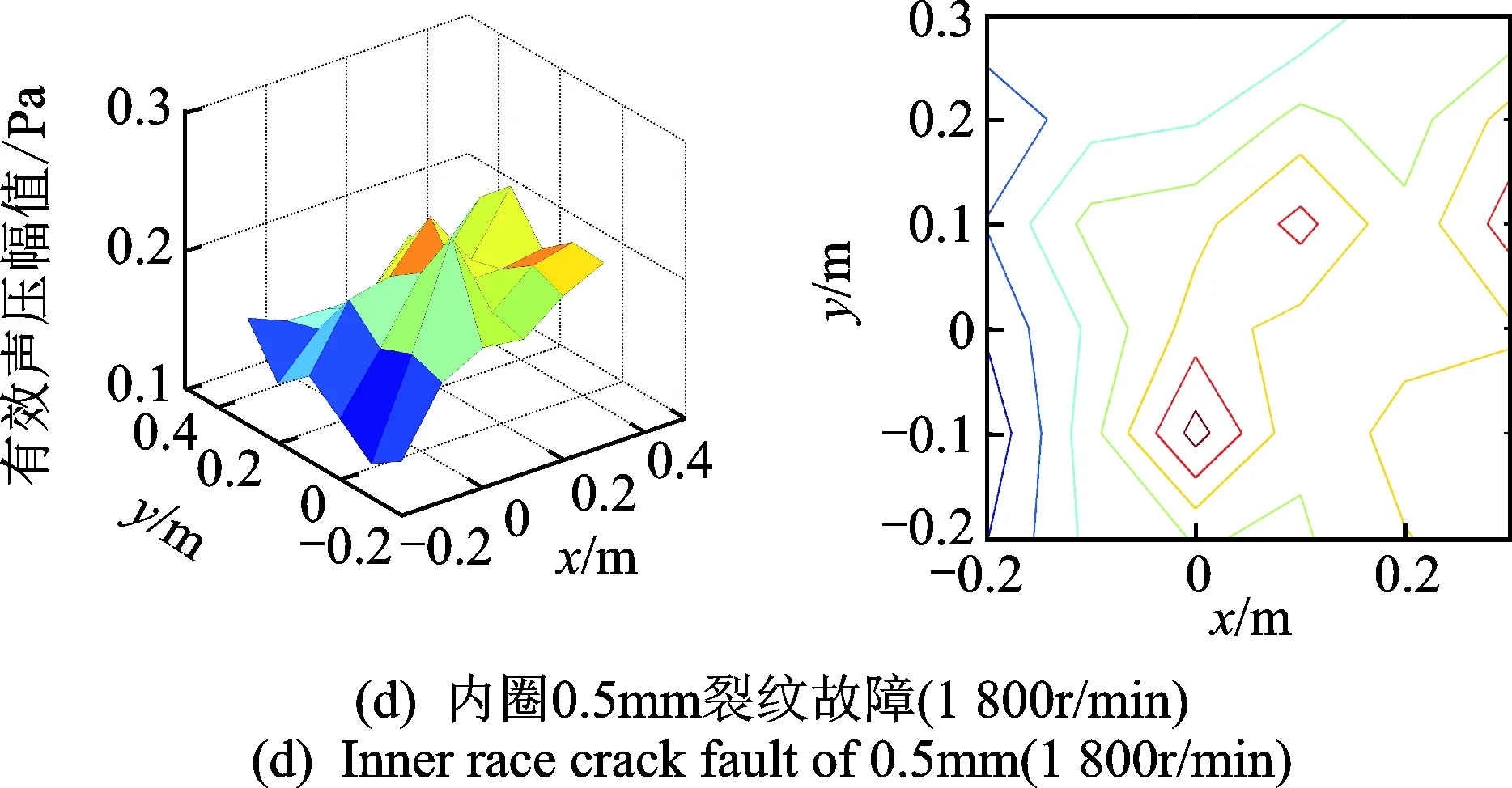
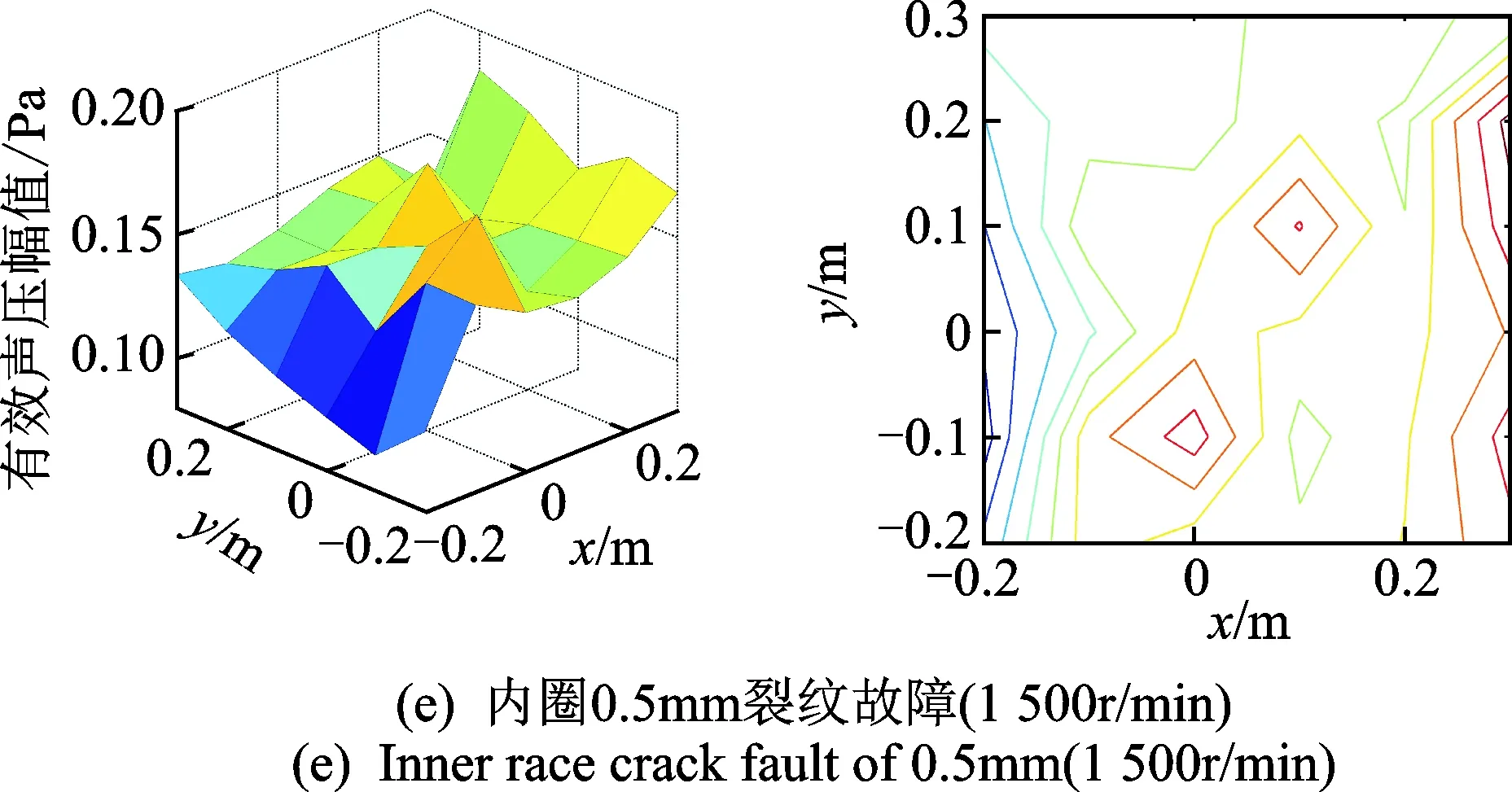
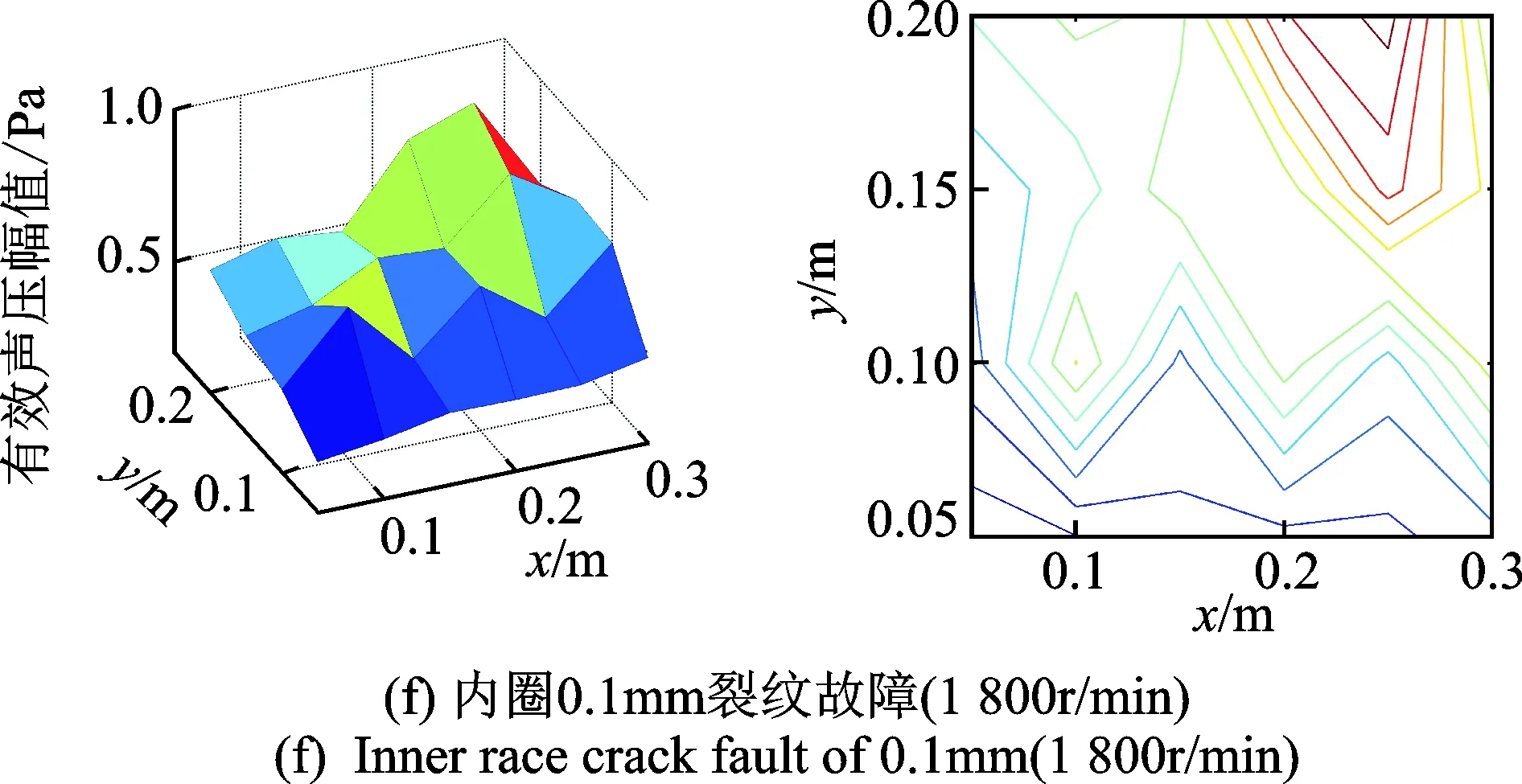
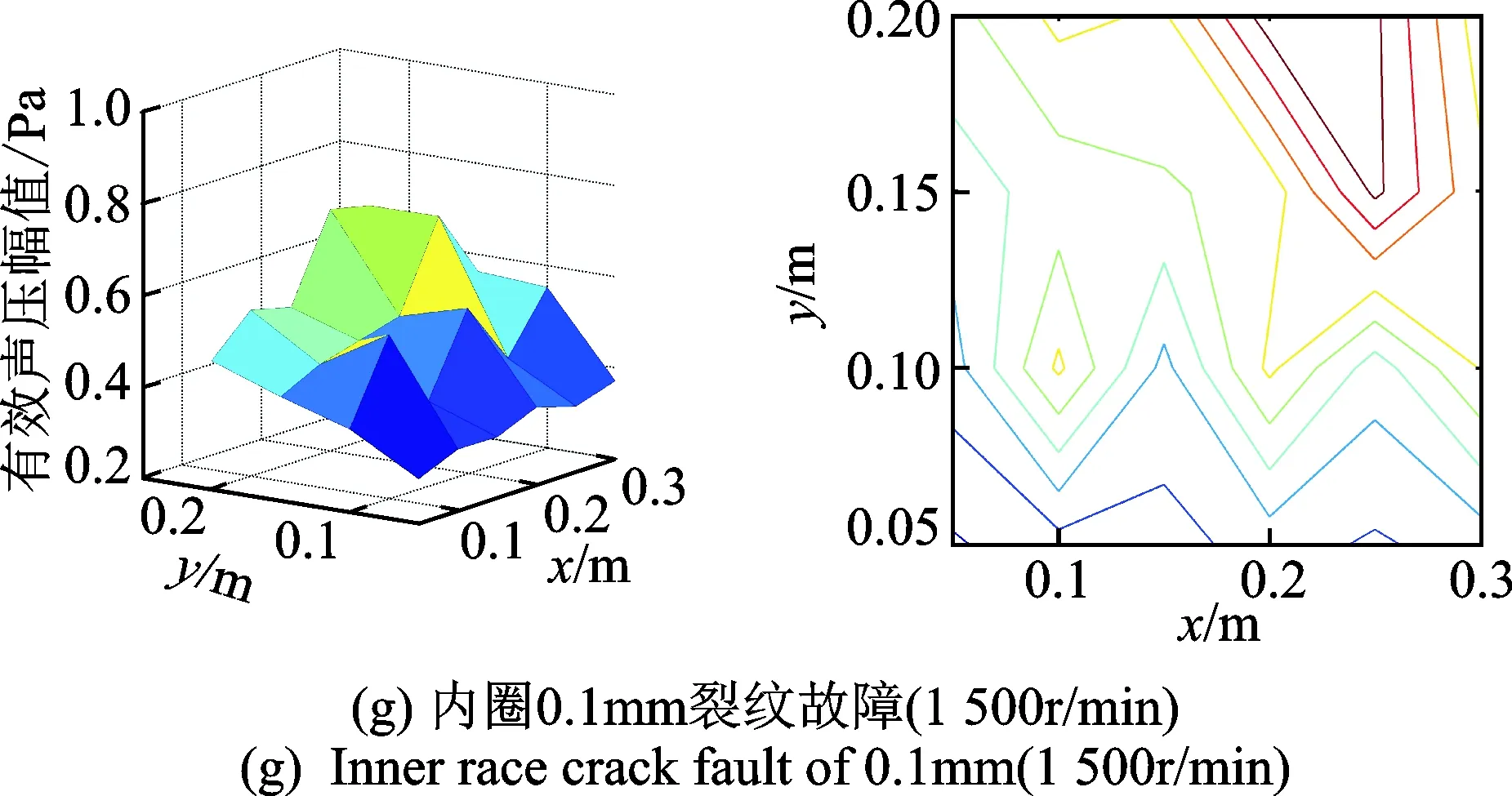
图7 不同工况下全息面有效声压场与投影图Fig.7 Effective sound pressure fields and projections of holographic planes under different working conditions

4) 图7(f)和(g)中，当采用4×6阵列传声器测量内圈裂纹(0.1mm)故障轴承声场时，在坐标(0.25, 0.15)和(0.1, 0.1)处出现两个“热点”，与图7(d)和(e)的热点位置基本对应。

“热点”意味着主要噪声源位置，据此可初步判断关键部位轴承是否异常，为进一步识别轴承故障类型提供依据。

按噪声功率信噪比SNR=-15的方式在信号整个时域范围内添加高斯白噪声，模拟外界干扰以形成信噪比很差的实际工况。利用Hilbert频谱分析和笔者提出的方法处理故障轴承不同工况下所对应的“热点”声信号，并将稀疏分解前后的时域图与Hilbert频谱图进行对比分析。

图8和9分别为外圈裂纹(0.5mm)故障轴承在转速为1 800和1 500r/min时的声信号处理结果。图8(a)为半消声室内测得转速为1 800r/min时外圈轴承故障声信号的时域图及Hilbert频谱图，可以看到明显的周期性冲击，其Hilbert频谱图呈现出清晰的外圈故障特征频率107.1Hz及2～4次谐波。对两种转速下的加噪信号进行处理，稀疏分解前后的时域图与Hilbert频谱图如图8(b)，(c)和9(a)，(b)所示。图8(b)和9(a)时域图中噪声较大，完全掩盖了故障特征，因受到杂频和噪声干扰，即使从其Hilbert频谱图也只能依稀识别出外圈故障特征频率(分别为107.1和89.19Hz，接近相应的理论值)。图8(c)和9(b)为稀疏分解处理得到的冲击信号。可以看到，在信噪比很差的情况下，稀疏分解提取到了明显的周期性冲击，噪声已基本被去除，其Hilbert频谱图呈现出清晰的外圈故障特征频率(分别为107.1和89.21Hz)及2～5次谐波，故障频率峰值也更加凸显。

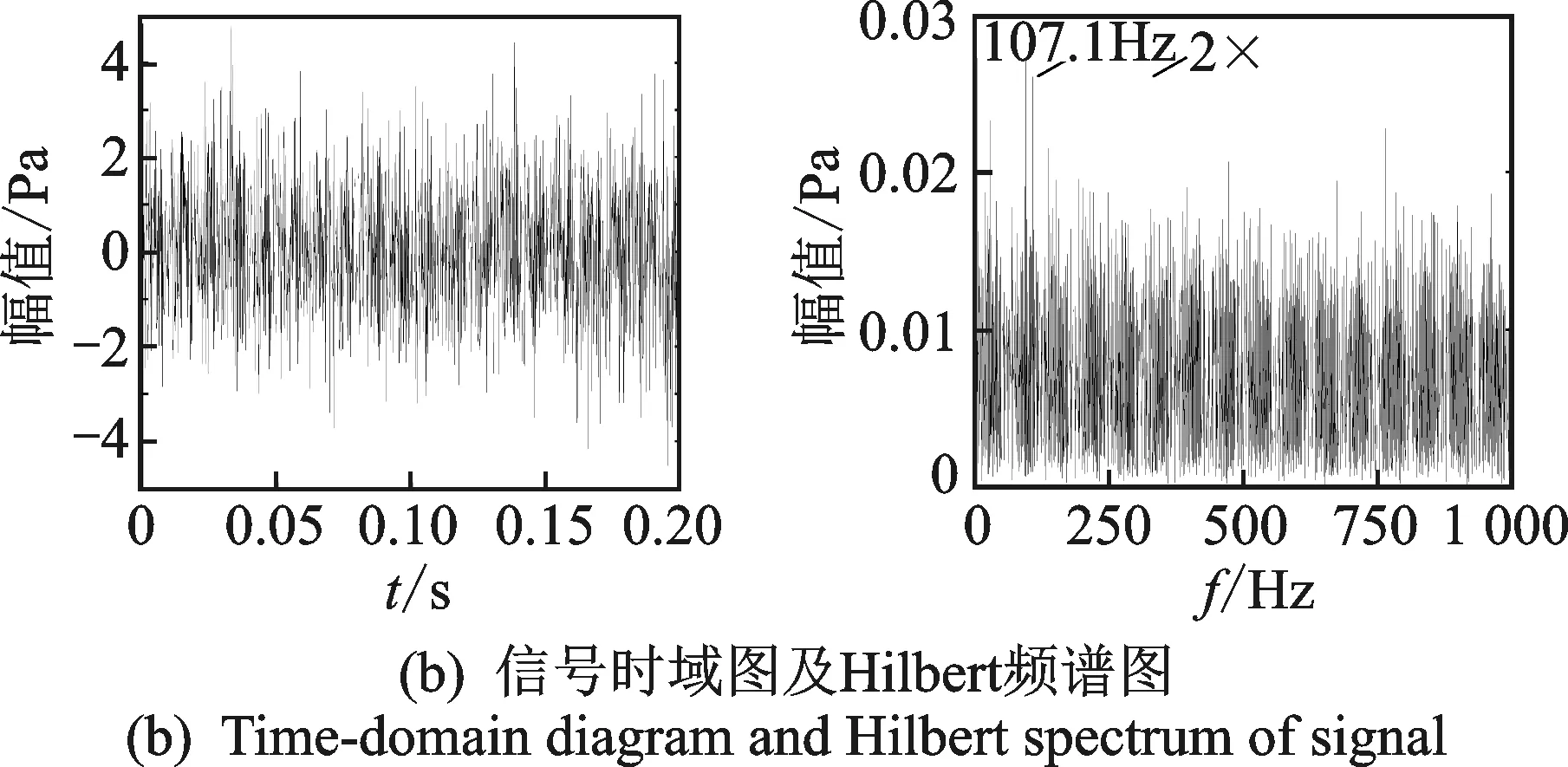
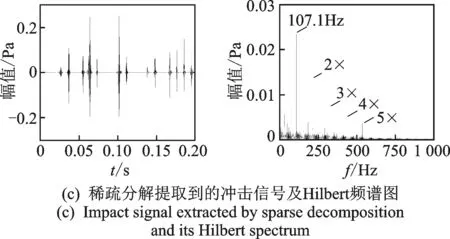
图8 外圈0.5mm裂纹故障分析(1 800r/min)Fig.8 Analysis of 0.5mm outrace crack fault (1 800r/min)

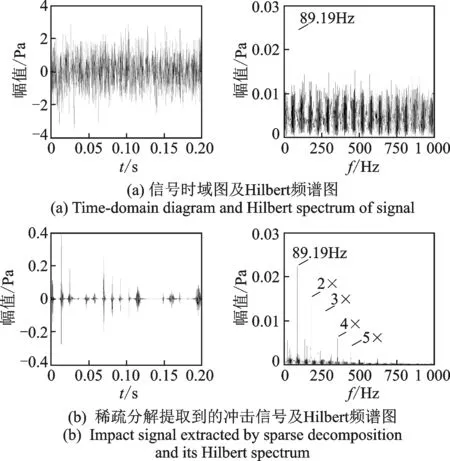
图9 外圈为0.5mm裂纹故障分析(1 500r/min)Fig.9 Analysis of 0.5mm outrace crack fault (1 500r/min)

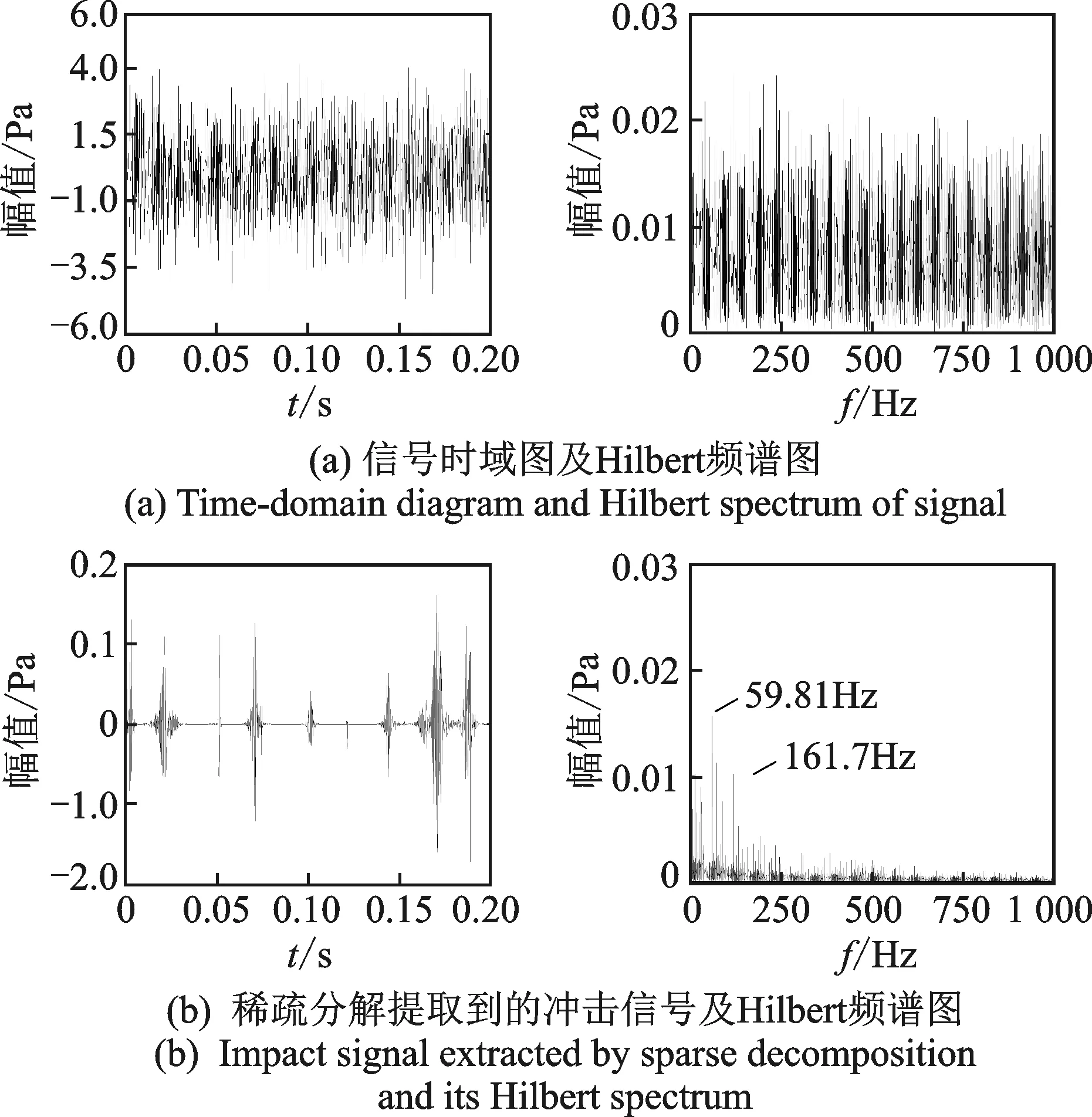
图10 内圈为0.5mm裂纹故障分析(1 800r/min)Fig.10 Analysis of 0.5mm inner race crack fault (1 800r/min)

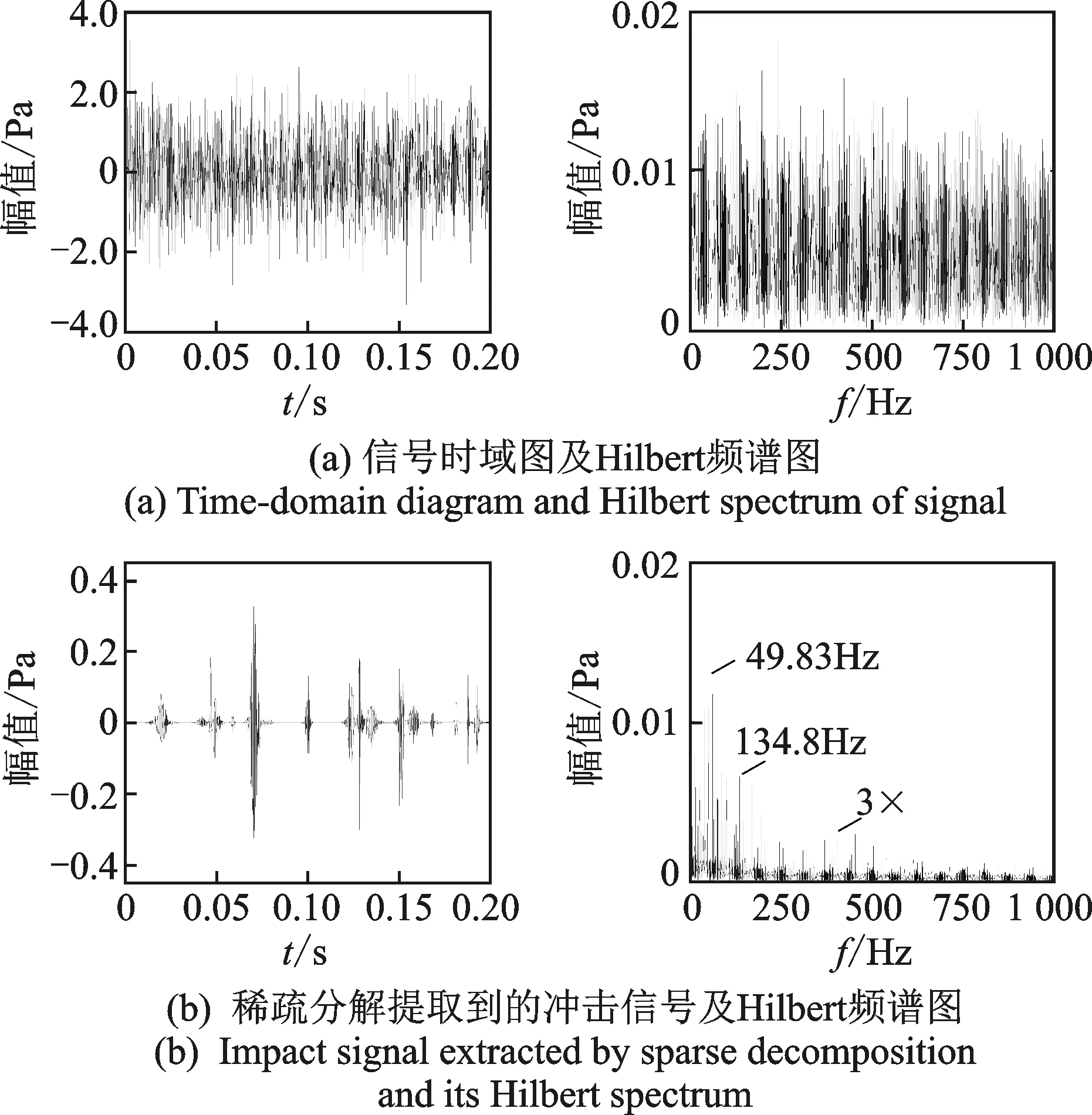
图11 内圈为0.5mm裂纹故障分析(1 500r/min)Fig.11 Analysis of 0.5mm inner race crack fault (1 500r/min)

图12 内圈为0.1mm裂纹故障分析(1 800r/min)Fig.12 Analysis of 0.1mm inner race crack fault (1 800r/min)

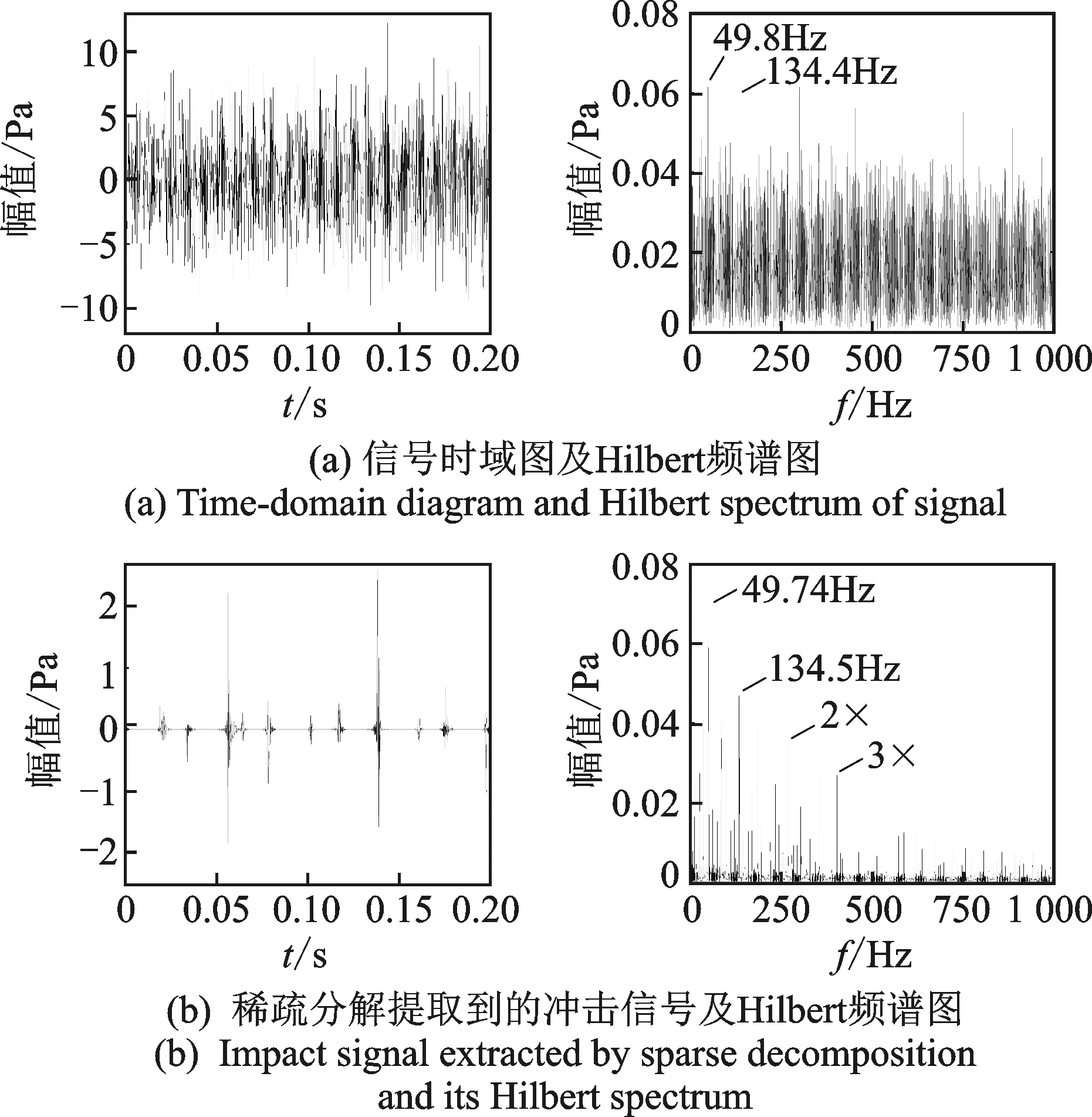
图13 内圈为0.1mm裂纹故障分析(1 500r/min)Fig.13 Analysis of 0.1mm inner race crack fault (1 500r/min)

图10和11分别为内圈裂纹(0.5mm)故障轴承在转速为1 800和1 500r/min时的加噪声信号处理结果。由图10(a)和11(a)可知，从时域图和Hilbert频谱图均无法判断轴承故障类型。从图10(b)和11(b)稀疏分解处理得到的冲击信号时域图中可看到明显的周期性冲击，噪声已基本被去除，并且其Hilbert频谱图中相应的二倍转频59.81和49.83Hz以及故障特征频率161.7和134.8Hz的峰值也更加凸显。

图12和13为内圈裂纹(0.1mm)故障轴承在转速分别为1 800和1 500r/min时的加噪声信号处理结果。由图12(a)和13(a)可知，时域图和Hilbert频谱图仍然无法准确判断轴承故障类型。从图12(b)和13(b)稀疏分解处理得到的冲击信号时域图中可看到明显的周期性冲击，噪声已基本被去除，并且其Hilbert频谱图中相应的二倍转频59.92和49.74Hz以及故障特征频率161.9和134.5Hz的峰值也更加凸显。

实例分析可见，在不同的故障类型和转速下，传统的Hilbert包络谱分析只能勉强甚至完全不能提取出故障特征，而稀疏分解方法在强噪声干扰下有效提取了轴承声阵列信号的故障特征，识别出了相应的故障，验证了该方法的可行性。

5 结束语

利用传声器阵列对轴承滚道缺陷故障进行检测，结合全息技术与稀疏分解算法的优点，提出一种基于稀疏分解的轴承声阵列信号特征提取方法。利用仿真分析证明了此方法在强噪声背景下提取轴承故障声信号特征的有效性。

在半消声室内搭建了轴承声阵列信号故障诊断实验平台，利用正常、内外圈故障轴承进行实验研究，对比分析了不同工况下得到的全息面三维有效声压场、提取的冲击信号时域图和Hilbert频谱图。结果表明，与传统的Hilbert包络谱分析方法相比，本研究方法消除了声信号中的噪声干扰，提取到了清晰的冲击特征，其Hilbert频谱图中故障特征频率峰清晰，可准确识别轴承故障类型。