基于EWT和多尺度熵的高压断路器故障诊断
2018-08-25万书亭豆龙江刘荣海
万书亭, 豆龙江, 刘荣海, 张 轩
(1.华北电力大学机械工程系 保定,071003) (2.云南电网有限责任公司电力科学研究院 昆明,650000) (3.华北电力大学图书馆 保定,071003)
引 言
高压断路器作为电网运行的重要设备,具有控制与保护的作用,高压断路器性能的可靠性关系到整个电网运行的安全与稳定。电力设备的在线监测和快速诊断的发展推动着智能电网的建设,为了改善以往定期巡检带来的负面影响,加强对断路器运动时产生的振动信号的研究,提前发现潜在故障,对提髙断路器运行的可靠性以及加强电力系统的稳定性具有重要意义[1-2]。
高压断路器在合闸或分闸过程中产生的机械振动信号蕴含了丰富的操作机构状态信息,针对其振动信号展开分析可发现断路器操作机构的螺丝松动、铁芯卡涩等故障信息[3-5],因此,基于振动信号的故障诊断与状态识别逐渐成为研究热点[6-11]。文献[12]采取希尔伯特-黄变换,采用经验模态分解(empirical mode decomposition,简称EMD)处理高频分量,根据分解后的各固有模态函数能量分布特点对断路器故障进行分类,验证了该方法的有效性。文献[13]将小波包和径向基神经网络相结合用来对断路器振动信号进行特征提取和模式识别,取得了一定效果。文献[14]使用因子分析对特征量进行降维优化、支持向量机经粒子群参数寻优后对断路器的状态进行分类,取得了较好的效果。文献[15]提出了基于经验模态分解能量总量法与SVM相结合的断路器振动信号的特征向量提取和故障分类的方法,并验证了方法的有效性。但这些诊断方法仍存在一定的不足,例如,EMD 和集合经验模态分解(ensemble empirical mode decomposition,简称EEMD) 均采用与小波结构相类似的递归筛分算法,二者缺乏完备的数学理论,分解得到的模态数量较多,且每个模态的筛分需要多次迭代,筛分计算量较大。应用小波包分析信号必须选定基函数和分解尺度,基函数的选择影响着计算的效率和分析的有效性,不同的基函数造成分析结果的不同,具有一定的局限性。Gilles[16]基于小波变换和窄带信号分析理论,给出了EWT的运算过程。EWT理论依据完备且计算量远小于EEMD 和EMD,其本质是通过对信号频谱进行自适应地分割,构造合适的小波滤波器组,从而提取信号的不同调频调幅成分。该方法已成功应用于信号处理和图像降噪分析中[17-19]。研究表明,EWT不仅避免了端点效应和模态混叠现象,还提高了信噪比、加快了计算速度。
经查阅国内外文献,鲜有学者将EWT引入到断路器故障诊断与状态识别中,笔者尝试利用经验小波变换处理断路器分闸过程中振动信号,从信噪比较低的原始信号中提取出包含特征信息的信号分量,然后引入多尺度熵作为信号的特征向量,最后利用SVM完成状态识别与分类。研究结果表明,该方法可快速准确的提取断路器故障特征,并完成断路器故障的状态识别。
1 EWT原理
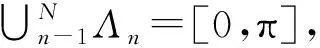
(1)

(2)
其中:τn=γwn;γ=minn[(wn-1-wn)/(wn+1+wn)];β(x)=x4(35-84x+70x2-20x3)。
在经验小波变换方法中,选择合适的算法对振动信号的傅里叶频谱进行分割至关重要,直接影响自适应分解的结果。完成自适应分解后,各自的频
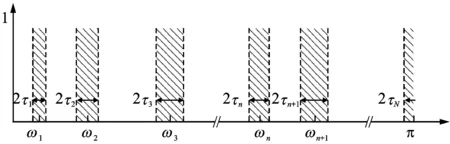
图1 傅里叶坐标系的分割Fig.1 Partitioning of the Fourier axis
谱对应不同特定紧支撑频率为中心的模态[20]。将Fourier支撑[0, π]分割成N个连续的部分,除去0和π,还需确定N-1个边界。笔者采取通过在频域范围内检测幅值的极大值,按照从大到小的规律排列,取前N-1个极大值点选择合适的算法确定边界。
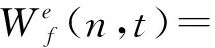
(3)
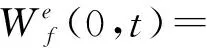
(4)
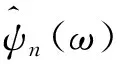
原始信号重建为
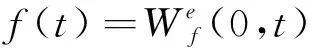
(5)
经验模式fk(t)可定义为
2 多尺度熵
多尺度熵(multi-scale entropy, 简称MSE)的计算步骤如下。
1) 假定原始序列为{x(i)=x(1),x(2),,x(N)},通过人为设定嵌入维数m和相似容限r,建立新的粗粒序列
(8)
其中:τ=1,2,为尺度因子。
当τ=1时,yj(1)就是原序列。非零整数τ,序列Xi被割分成N/τ个长为τ的粗粒序列yj(τ)。
2) 对获得的N/τ个粗粒序列求样本熵,并作为尺度因子τ的函数,由此定义多尺度熵,即
MSE(x,τ,m,r)=SampEn(yτ,m,r)
(9)
样本熵在描述时间序列时的复杂程度为单一尺度,熵值的大小代表了时间序列的复杂程度。多尺度熵实质上相当于在不同尺度下计算时间序列的样本熵。若随着尺度因子增加,时间序列的熵值单调递减,则说明数据结构相对规则,在小尺度上包含更多状态信息;反之则说明数据结构相对复杂,在大尺度上包含更多信息。
3 支持向量机原理
SVM是一种基于小样本训练的学习算法,以结构风险最小化为原则,工作原理如图2所示。图中:圆点和方点分别为不同的数据样本;H为分类线,可以把两类样本准确分开;H1,H2为与H相平行且通过离分类线最近的样本的直线。H1与H2之间的间隔为分类间隔,如图2中方点标出的样本所示,因其支持了最优分类面故称为支持向量。

图2 最优分类面Fig.2 Optimal separating hyperplane
4 实验应用分析
4.1 实验模拟
在断路器无载的情况下,摘除缓冲弹簧模拟缓冲弹簧无效故障、调节传动杆长度模拟传动机构故障、松动基座螺丝模拟基座螺丝松动故障,故障模拟如图4所示。
在正常状态下和3种故障状态下分别进行6次实验,数据采集器在断路器进行分闸操作时以10 kHz的速率采集5 000点,共得到24组数据。分闸过程中典型振动信号如图5所示。

图3 高压断路器振动测试实验Fig.3 Experiment of high voltage circuit breaker

图4 故障模式模拟实验Fig.4 Simulative experiments of fault patterns
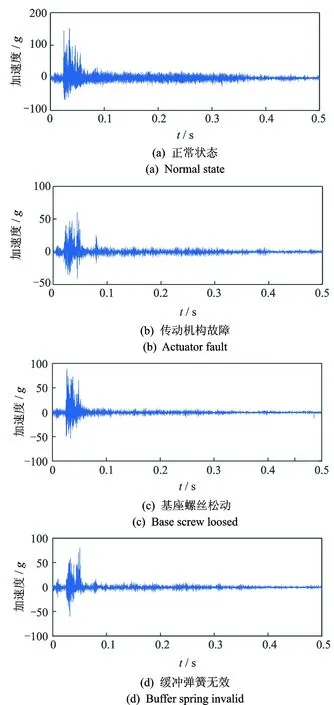
图5 高压断路器振动信号Fig.5 Vibration signal of high voltage circuit breaker
从图5可以看出,在时域内观察4种状态下断路器振动信号虽然存在一定的差异,但没有明显的变化规律,因此考虑引入经验小波变换处理断路器振动信号,从信噪比较低的原始信号中提取出包含特征信息的信号分量,然后提取各自多尺度熵作为信号的特征向量,最后利用SVM完成高压断路器的状态识别与分类。
4.2 振动信号分析
以基座螺丝松动振动信号为例,分别采用EEMD和EWT对其进行处理,分解得到的IMF如图6所示。可以看出,EWT分解得到6个IMF,运行时间为0.517 s,每个IMF波形与原始振动信号大致相同;EEMD分解得到13个IMF,运行时间长达35.449 s,显然增加了EEMD的迭代次数,存在虚假模态和模态混叠的现象,不利于提取振动信号特征。采用EWT处理断路器振动信号,不仅避免了模态混叠现象,还加快了计算速度,具有明显优势。
4.3 特征参数提取
利用经验小波变换分别对4种状态的振动信号进行分解,经过多次实验分析,选择与原始信号相关系数最大的3个固有模态分量进行重构。对重构信号进行熵值求解,每种断路器状态各取3组数据,计算数据的样本熵并求其平均值,如表1所示。

表1 4种状态信号的样本熵值
从表1可以看出,不同故障状态振动信号样本熵大小不同,同种故障状态振动信号样本熵值在平均值附近来回波动。通过对4种振动信号样本熵大小的对比发现,正常状态和传动机构故障的样本熵值相对较大,说明这两种状态振动信号的时间序列相对不规则、复杂性较高。基座螺丝松动和缓冲弹簧无效样本熵值相对较小,代表了这两种状态振动信号时间序列相对较规则、复杂性较低。整体来看,样本熵基本可以实现断路器故障特征的提取,但也存在各种状态的样本熵值相差不大、个别出现交叉重叠的问题,故障特征不明显。
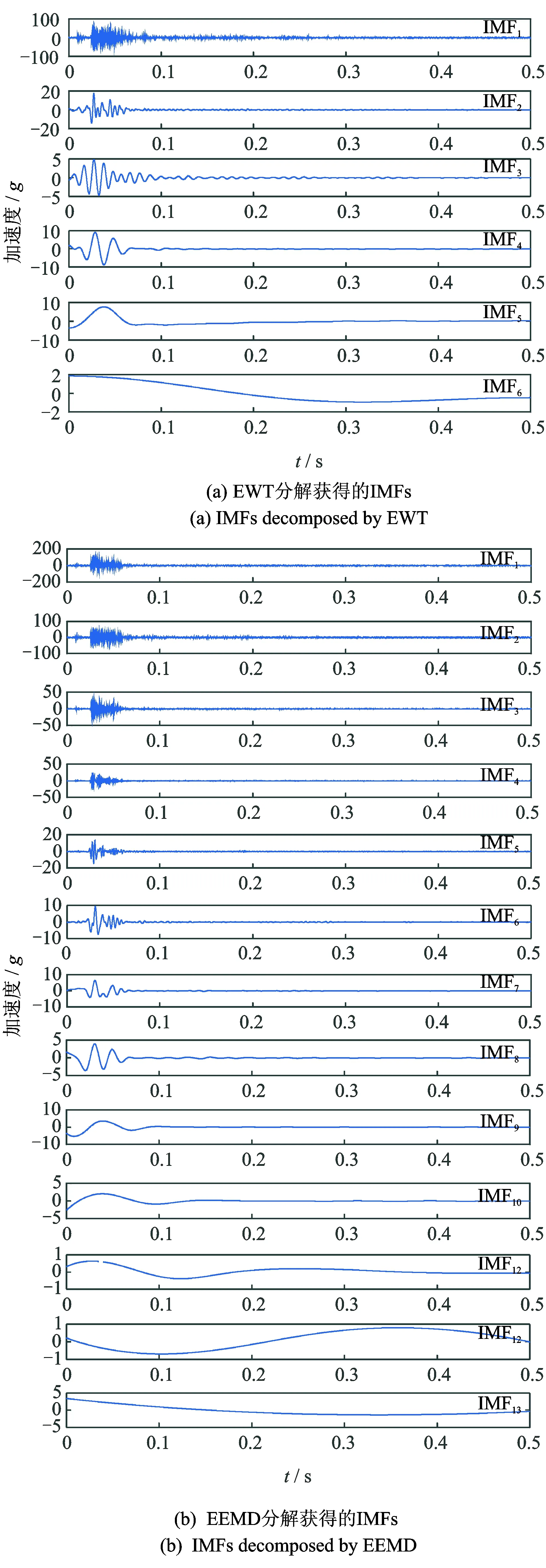
图6 EWT和EEMD分解结果比较Fig.6 Comparison between the results of EWT and EEMD decomposition
从表1可以看出,对原始振动信号求取样本熵值其实是在单一尺度下时间序列的熵值,尽管不同状态的样本熵值不同,能够区分出断路器对应的状态,但是个别熵值较接近区分效果不明显。因此对于振动信号的分析引入多尺度熵,将分析结果绘成尺度因子的函数关系图,如图7所示。
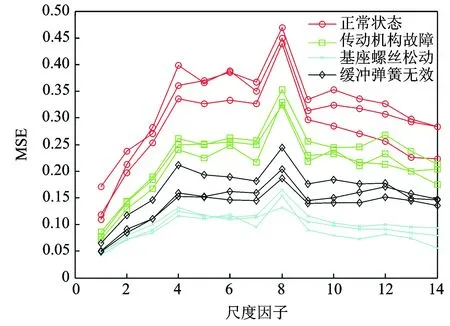
图7 4种状态信号的多尺度熵Fig.7 Multi-scale entropy of four kinds of signals
从图7可以看出,对于断路器的振动信号分析引入多尺度熵后,4种状态的熵值大小排列与样本熵值大小排列相一致;随着尺度因子的变化,断路器4种状态熵值的变化非常直观地显示出来,同种状态的多尺度熵值变化规律一致、熵值大小均在同一区域范围内波动。从多尺度熵值变化图中区分故障类型非常明显与直观,相对于样本熵采用多尺度熵分析具有无可比拟的优越性。
随着现代水产养殖行业的进步和发展,在快速进步条件下,消费者对水产品的需求也产生明显变化。其中,保证水产品质量的提升,增加其需求量十分必要。受到季节性因素的影响,在一定需求下,可以将其转变为常年需求。所以,要将市场作为导向,保证水产养殖品种的优化,确保优质化水产品种的推广,在这种建设条件下,不仅能符合市场的建设需求,也能为水产养殖效益提供合理途径。比如:对当前的水产养殖品种进行开发与利用,引进种植新品种。还需要对养殖周期做出详细思考,提高市场价格,保证群众都能加强对水产品种的认识,也要根据地区的实际发展情况,促使整个生产规模的壮大化发展。
4.4 模式识别与分类
断路器本身的工作特性决定了其不能频繁的动作,实际实验采集的测试数据量有限,测试样本数较少,不利于故障识别训练。传统使用的专家系统以及神经网络方法需要较多的测试样本,样本越多,识别结果准确。支持向量机是一种基于小样本训练的识别方法,更适合于断路器故障的状态与分类[21]。这里使用林智仁教授提供的支持向量机工具livsvm 3.21版,分类采用“一对其余”策略,考虑断路器正常工作状态及可能出现的故障,构建4个支持向量机即4种运行状态,最终结果由分类距离最大的向量机决定。
在支持向量机各项参数中,核函数的选取至关重要。由于径向基函数模型简单、参数少,故选择径向基函数作为核函数。除了核函数外,需要选择相对较佳的惩罚参数C和核函数参数g来提升支持向量机的分类性能。笔者选择网格搜索算法进行参数优化寻找最优的C和g,即尝试各种可能的C和g值,然后交叉验证,得出最优惩罚参数C为16、核函数参数为2。在此参数下,用训练集样本数据训练支持向量机,使用训练好的支持向量机对测试集样本数据进行分类测试,测试样本共8组数据,每种运行状态2组数据,与训练集数据不重叠。测试结果如图8所示。标签1~4分别代表正常状态、传动机构故障、基座螺丝松动和缓冲弹簧无效4种状态。可以看出,测试集中8组数据的分类结果与实际类别一致,分类准确率为100%(8/8)。
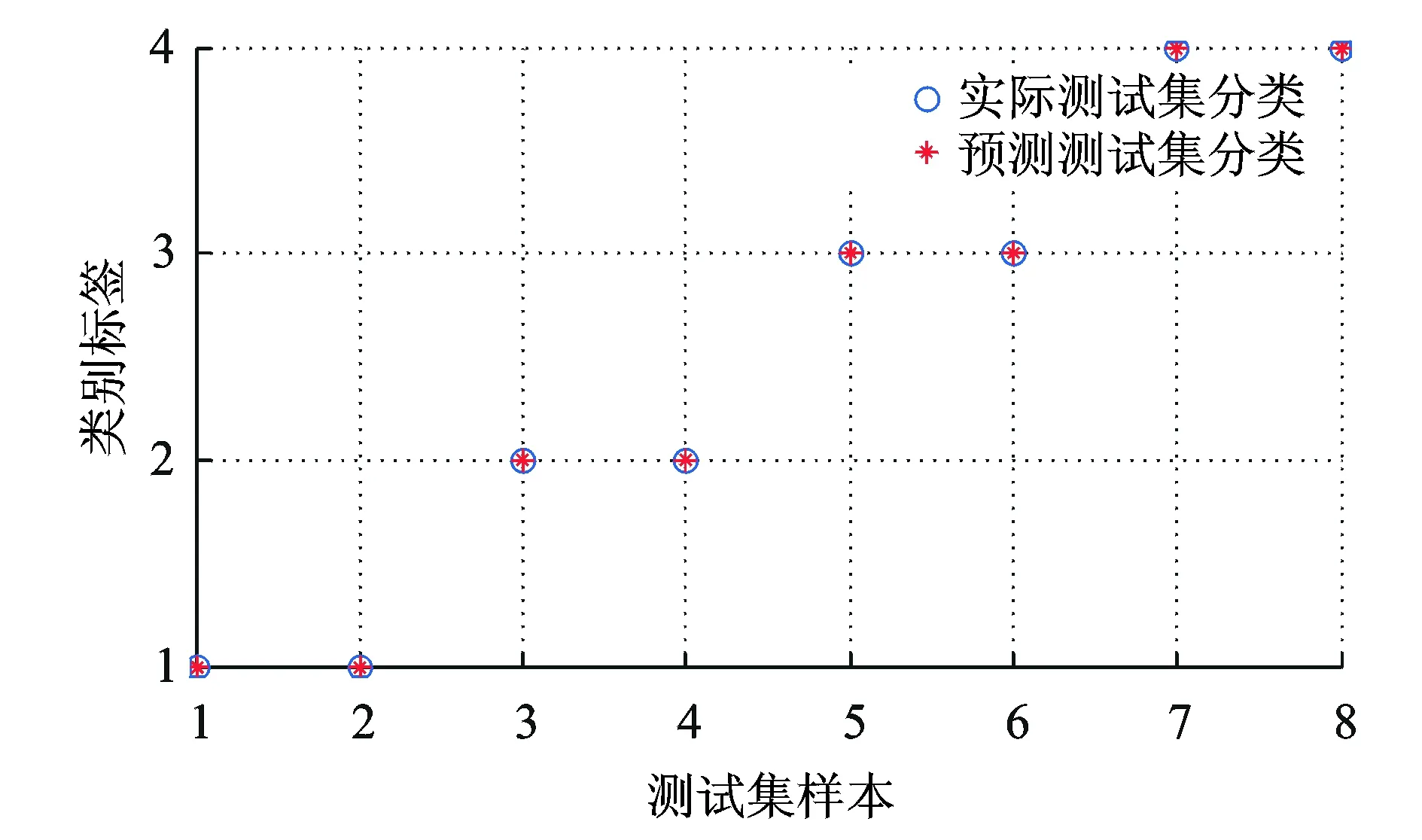
图8 实际分类与预测分类对比图Fig.8 Comparison chart of actual classification and prediction classification
该结果表明,采用经验小波分解、多尺度熵特征值提取、网格参数优化和支持向量机分类在内的振信号特征提取和诊断方法能够准确地实现断路器故障实验中各种状态的分类。
5 结 论
1) 将经验小波分解和多尺度熵相结合的方法首次应用在高压断路器振动信号的分析中。该方法不仅降低了模态混叠和虚假模态现象对特征提取的影响,而且大幅加快了计算速度,具有明显优势。
2) 通过多尺度熵与样本熵的对比分析得出,从多尺度熵值变化图中可以更直观、更明显地区分断路器故障类型,将振动信号的多尺度熵值作为特征参数有利于断路器状态识别及故障分类,对以后断路器的研究提供有益参考。
3) 研究结果表明,本算法能有效提取断路器故障振动信号的特征向量,并能正确地进行状态识别与分类,提高了分类精度,取得了较好的诊断效果,为断路器故障诊断与状态识别提供了新的思路。
