基于数字图像及随机最小二乘的红提串果粒尺寸检测分级方法
2018-08-24王巧华
肖 壮,王巧华*,王 彬,许 锋,杨 朋,李 理
(华中农业大学工学院,湖北 武汉 430070)
目前,机器视觉技术被广泛应用于工业、医学、农业等领域[1-5],在对农产品的尺寸检测方面,国内外学者做了不少的研究:周竹等[6]设计了一种V型平面镜马铃薯分级系统,提出了一种最小外接柱体体积法来计算马铃薯的尺寸大小,并按照大小分级准则将马铃薯分为大、中、小3 个等级,实验最终分级正确率为91.0%。Marchant等[7]设计了一套基于机器视觉的对土豆大小和形状分级的系统,其处理速度基本满足了在线的要求。邓海霞等[8]应用图像处理技术对群体鸡蛋进行单个识别,并通过一元线性回归的方法分析了鸡蛋图像面积与实际质量、实际长短轴与图像中的长短轴的线性关系,模型的相关系数分别达到了0.92、0.91和0.94。
葡萄作为世界第二大栽培水果,深受人们的喜爱,我国对葡萄的尺寸分级仍然采用人工分级的方法,其对柔软的果粒具有较大损伤,且分级效率极低;因此,应用机器视觉技术对葡萄进行无损尺寸分级具有广阔的应用前景。由于红提葡萄为穗状结构,且果粒之间相互堆叠,多数果粒遮挡严重,因此应用机器视觉技术对葡萄果粒识别并进行尺寸分级有较大的难度。曾庆兵等[9]通过形态学处理的方法,实现了对葡萄果粒的精确定位,从而为观测葡萄的生长状况提供了参考;Li Min等[10]通过检测葡萄轮廓的角点将轮廓边缘的葡萄果粒识别出来,并通过计算单粒葡萄的平均曲率作为判定标准,将葡萄按照大小分级,最终分级准确率为90%;陈英等[11]通过判定和识别轮廓线上的凹点,并将凹点之间的弧段作为葡萄果粒的轮廓,从而拟合出葡萄轮廓边缘上的葡萄果粒,该算法对整串葡萄的识别率为35%,大小分级正确率为72.7%;Roscher等[12]通过采集自然环境下的葡萄穗图像,采用Hough检测圆的方法检测所有可能的近球葡萄,通过颜色、纹理等信息设计分类器,检测出葡萄的果径大小,其相关系数为0.88;李敏[13]提出了一种红提果粒的检测算法,通过在轮廓边缘上选取距离一定的3点,采用最小二乘椭圆拟合的方法获得果粒尺寸,其正确率为85.14%。
由上述研究可以看出,国内外对农产品的尺寸研究并不鲜见,但是像葡萄这样的具有穗状结构且果粒密集的水果尺寸研究却存在难度。上述关于整串葡萄的研究也只通过提取边缘轮廓上的果粒,而边缘果粒不能代表整串果粒,随机性太大,正确率不高,这也是目前葡萄尺寸大小检测面临的瓶颈问题,亟待解决。本研究以葡萄的一个品种——新疆红提为研究对象,采用了基于形态学重构和局部极大值的方法,通过红提表面的亮度信息,识别和定位红提串整个外表面的果粒,通过梯度分割的方法,获得准确的红提轮廓,再采用随机最小二乘椭圆检测的方法对果粒进行拟合,并提取尺寸参数,以期实现对整串红提的尺寸分级。
1 材料与方法
1.1 材料
新鲜新疆红提购自华中农业大学水果超市。
1.2 仪器与设备
本实验图像采集系统如图1所示,光室为尺寸为600 mm×450 mm×450 mm的箱体,在暗箱顶部设置有滑道,葡萄悬挂于滑道下端的挂钩上,通过手动控制葡萄与相机间距离,以采集到最清晰的图像;AD-080GE的双通道工业相机(分辨率为1 024×768,帧率为30 fps,能同时采集红-绿-蓝(Red-Green-Blue,RGB)图像和近红外(near infrared,NIR)图像) 丹麦JAI公司;LM6NC镜头 日本Kowa公司。

图 1 图像采集装置Fig. 1 Schematic illustration of the image acquisition device
1.3 方法

图 2 原始图像Fig. 2 Original images
1.3.1 图像处理采集到某串红提RGB图像和NIR图像如图2所示,由原始图像可以看出,RGB图像中红提与背景颜色都呈现深蓝色,相邻果粒之间颜色差距不大,边缘轮廓不明显,但果粒与果梗间有明显的颜色区分;NIR图像中红提与背景颜色差距很大,果粒的轮廓明显,但其果粒与果梗颜色相近。故本研究在RGB图像中进行果梗的去除,在NIR图像中进行果粒的轮廓提取。
1.3.1.1 果梗的去除


图 3 去除果梗Fig. 3 Images without stalks
红提串中存在大量的绿色果梗,由Sobel算子获得的红提轮廓图像(图3a)可以看出,果梗的轮廓会严重干扰到周围红提果粒的检测,属于干扰信息,故必须删除。果梗的颜色为绿色,常见的绿色信息图像分割的方法为HSV(Hue-Saturation-Value)彩色图像分割法[14-16],由于HSV色彩空间相比于其他色彩空间是最接近人眼的,通过统计HSV图像中的H色调值选取合适的阈值,可以大致分割出绿色像素点,但该方法对阈值的选取要求高,且H色调值是根据统计获得的,绿色的色调值位于HSV空间中的60°~180°之间,对应于HSV模型中的0.16~0.50之间,取值范围较大,且红提表面的纹理及斑点会严重影响到其颜色的折射率,故这种方法去除红提果梗的效果较差,选取不同的阈值范围,采用HSV彩色图像分割的方法去除果梗的效果如图3i~k所示。基于果梗在RGB彩色空间中G分量所占比例较大,通过实验对比了G-B、2G-R-B、2g-r-b的转换效果图[17],如图3l~n所示,发现归一化超绿法[18-19]的效果最好,其中r、g、b的计算如公式(1)~(3)所示。

式中:R、G、B分别为红色图像基于RGB色彩空间的红色、绿色、蓝色分量;r、g、b分别为归一化后的红色、绿色、蓝色分量。
归一化超绿法去除绿色果梗:分别提取红提RGB图像的R、G、B 3 个分量值并将其转换为r、g、b,如图3b、c、d所示,通过2g-r-b的色差计算,提取出果梗的灰度图,通过Otsu阈值法选取出最佳阈值,并将灰度图转为二值图,再通过膨胀处理扩大果梗区域。对果梗的二值图像进行取反处理后,将其与图3a进行图像的乘法运算,处理过程如图3b~h所示。
由图3i~n的去除果梗效果及处理的过程可以看出,归一化超绿法相比于其他去除果梗的方法来说,不需要人为设定阈值,算法简单可靠,能有效去除无用的绿色果梗信息。
1.3.1.2 红提果粒的定位

图 4 果粒的定位Fig. 4 Location of grapes
由图4a可以看出,红提串表面的果粒在光源的照射下产生了细小的亮点,且其大致在果粒的中心位置,故本研究将其作为红提定位的依据。若直接对NIR图像进行亮度局部极大值运算,得到的亮点效果图如图4b所示,其明显不能满足定位的要求,主要是因为果粒表面存在大量的果粉、细小的脏污点,并且在光源的照射下,果肉中的细小纹理都显露出。为解决这些问题,本研究采用了基于形态学的开闭重构算法[20-21],假设J和I分别为红提的参考图像和原始图像,I≤J,以参考图像J为变换的起点,通过原始图像I来规范不断变换的过程,直到红提灰度图像像素值保持稳定为止。膨胀重构和腐蚀重构[22]分别由公式(4)~(5)表示。
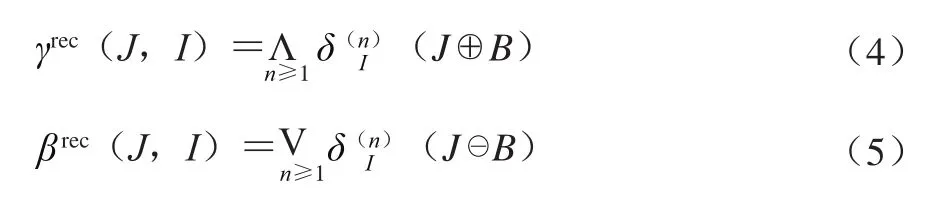
本研究使用了基于形态学的开闭重构运算,通过先开重构后闭重构的两次重构,参照膨胀和腐蚀重构的迭代方法,将混合开闭重构算法表示为式(6)。

1.3.1.3 边缘拟合
通过以上几个步骤处理后,已经初步获得了红提串表面的颗粒位置及图像轮廓,要想得到单粒红提的轮廓尺寸,需要对识别到的果粒进行检测。由于成熟红提果粒为非标准椭球形、果粒之间相互堆叠、红提表面存在光斑等干扰因素影响,若直接进行多椭圆检测,将会产生大量的无效计算且效果不佳;因此本研究采用基于梯度分割的随机最小二乘椭圆拟合的方法对红提进行拟合,即通过梯度分割的方法截取每粒果粒轮廓,再通过随机最小二乘椭圆拟合对果粒进行逐一拟合。
梯度分割:通过大量的统计红提图片,发现红提的外形处于半径范围在Rmin和Rmax的圆环内,故截取每粒红提在圆环范围内的像素点,其中一串中第8粒果粒及其处理结果如图5所示。

图 5 第8粒红提Fig. 5 The 8th grape
由图5可以看出,红提果粒相互堆叠,相邻果粒轮廓之间互相干扰,其严重影响到单粒红提的椭圆识别。经观察发现,属于不同果粒的轮廓线上的点的梯度方向差距很大,故引用了梯度法[24-26]。
梯度对应的是一阶微分,函数图像在某一点的梯度是一个向量,其方向与最大的方向导数相同,与边缘点方向垂直。在二维图像中,设f(x,y)为连续图像函数,其在点(x,y)处的梯度是一个矢量,其方向角按公式(7)计算。

在数字图像中,用差分来代替偏导数,由于边缘检测采用的是Sobel边缘检测的方法,故采用Sobel梯度差分法,图6a中显示3×3大小的区域灰度值,其中Z1~Z9分别表示3×3区域内的灰度值,图6b为两个偏导数的相应模版,每个数字对应Z1~Z9的卷积因子,计算边缘轮廓点偏导数Gx和Gy的公式如式(8)、(9)。
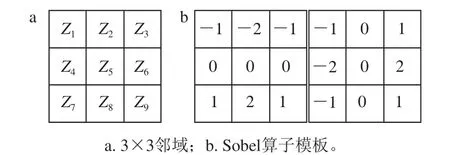
图 6 Sobel算子模型Fig. 6 Model of Sobel operator


将红提果粒近似看作球形,利用极坐标的形式来近似表示出红提果粒中心坐标(式(12)、(13))。

式中:rm为果粒半径的估计值;x、y为轮廓像素点的坐标值;a、b为边缘轮廓像素点所计算的圆心坐标值,将式(10)、(11)中的正弦、余弦值代入(12)、(13)即可计算圆心坐标值。
理论上,若像素点(x,y)为该圆轮廓的一部分,则a、b值必为圆心的坐标值,但由于大部分果粒轮廓为椭球形,且只知道定位圆心的估计值O(ai,bi),故可选取合适阈值δ,若由梯度计算而来的圆心坐标(a,b)与O(ai,bi)的距离平方的误差范围在[0,δ]内,可将像素点f(x,y)作为该粒红提的轮廓,否则去掉该干扰点,计算公式如式(14)所示。

式中:A(x,y)为该粒红提的真实轮廓。红提串中任意4 粒处理的效果如图7所示。

图 7 梯度分割后的果粒Fig. 7 Grapes after gradient segmentation
随机最小二乘椭圆拟合:最小二乘椭圆拟合是一种通过最小化误差的平方寻找椭圆点的最优估计技术[27-28]。通过梯度法去除干扰弧段之后,仍然存在有果粒轮廓重叠严重的现象,若直接使用最小二乘椭圆拟合的方法拟合果粒会出现较大误差,本研究采用随机最小二乘椭圆拟合的方法[29-30],具体的步骤如下。
1)将取得的第m粒果粒的轮廓边缘坐标存入坐标点集An中,设置最大迭代次数N,覆盖率阈值Pr,将可能的果粒边缘点集L0、L1设置为空集。
2)在边缘点集An中随机选取5 点坐标,若所取的5 点满足不共线,且任意两点之间相隔一定距离,则将5 点存入边缘点集Am中,若不满足条件,则重新选取5 点。
3)将边缘点集Am中的5 点进行最小二乘椭圆拟合,并得到可能的椭圆方程(公式(15))。

遍历边缘点集An中剩下的点带入公式(16)中。

式中:d代表第n粒果粒的边缘点集到可能椭圆的代数距离集合。统计集合d中距离小于阈值Ts的对应的像素点坐标并保存于L1中,若L1点集的个数占边缘点集An个数的比例大于覆盖率阈值Pr,则执行4),否则执行2)。
4)若点集L1的个数大于点集L0的个数,则将L1赋值于L0,否则,则将L1置空。
5)重复循环步骤2)~4),若循环次数n>N,则程序结束,获取轮廓边缘点集L0,并将其进行最小二乘椭圆拟合。
在图8中,分别用直接最小二乘法和随机最小二乘法对果粒1(图8a)和2(图8c)进行椭圆拟合,图8b和图8d为对应的拟合效果,红线为直接最小二乘拟合线,绿线为随机最小二乘拟合线。

图 8 两种算法的拟合效果比较Fig. 8 Comparison of fitting effects of two algorithms
由拟合效果可知,随机最小二乘法更能容忍样本点的差异,有较强的抗干扰能力。采用随机最小二乘的方法对整串红提进行拟合,其拟合效果如图9所示。

图 9 整串红提的拟合效果Fig. 9 Fitting effect of a bunch of grapes
2 结果与分析
2.1 红提尺寸参数转换
由于红提串表面果粒不在同一个平面上,其近似为一个球面,故不同位置的果粒距离镜头的距离也不一样,因此本研究采取分层转换的方法将红提的像素尺寸转换为实际尺寸,并根据红提的外层和内层分别计算。
如图10所示,遍历红提粒的中心,若其距离x或y方向上的红提串边界轮廓的最小值小于设定的阈值Dmin,则将其判定为外层果粒,否则为内层果粒。内外层果粒通过小孔成像的原理将像素尺寸乘以不同的系数转换为实际尺寸。
2.2 分级标准及方法验证
在实际生产中,红提人工分级方法是在红提串表面靠近底部随机选取10 颗红提果粒,用不同直径套圈来检测,出现次数最多的等级即为该串红提的等级。参照DB 65/T 2832—2007《红地球葡萄分级标准》(表1),其中后两行是对应的像素值分级标准。
本研究选取42 串成熟的新疆红提来验证本研究方法,再将实际尺寸分级标准转换为像素尺寸分级标准,并将其分级。在分级的过程中,采用15%幅度的降级原则,即被检测出的一级果偏多,但二级果占比超过15%,那么该串红提为二级果,依次类推。参照人工分级结果,使用本研究方法正确分级38 串红提,分级正确率达到了90.48%。其中第8串红提实验结果如表2所示。

表 1 红提大小分级标准Table 1 Criteria for grape size grading

表 2 第8串红提实验数据Table 2 Results of the detection of the 8th grape
3 讨 论
本研究采用基于图像处理的方法对整串红提进行大小尺寸的分级,正确率达到了90.48%。出现错判的原因可能有:在果粒的定位方法中,依据果粒的反光特性,运用基于形态学的开闭重构运算获得果粒中心的大致位置,但由于不同的红提串果粒的紧密度不同,有的果粒可能被遮挡较为严重,此时应用该算法检测不到反光点,故无法定位到该果粒,导致提取到的该串有效果粒样本数量减少,这可能造成分级错误。此外,在拟合果粒的方法中,采用随机最小二乘的方法能有效地拟合出图像中的果粒,相比与其他算法效果更好,但在实际实验中,果粒的形状并非标准的椭圆,且少量为畸形,连人工测量也无法准确获得其尺寸,这也使实际结果与测量结果有差异,从而导致分级错误。
采用归一化超绿法能有效地去除红提串中绿色果梗信息,相比于其他方法,其更简单,且具有鲁棒性和准确性。
基于形态学的开闭重构算法不仅能使果粒表面细密纹理和部分噪声引起的伪局部极小值被去除,并保留重要的亮度极值信息,根据亮度极值区域能有效地定位红提串表面的果粒。
在提取单粒果粒时,采用梯度分割法的方法能去除大部分目标果粒以外的干扰弧段,缩短后续椭圆检测的运算时间。由于红提的形状为非标准椭圆,且存在少量覆盖严重的干扰弧线,若直接进行最小二乘椭圆拟合将产生较大偏差,本研究采用随机最小二乘椭圆检测的方法,通过约束点与椭圆的代数距离,获取有效的边缘点,使红提轮廓精准拟合,实现了整串红提的正确分级,分级准确率为90.48%。
