由2018年北京理综第20题引起的讨论

张 适

(北京市育英学校，北京 100036)

原题.根据高中所学知识可知,做自由落体运动的小球,将落在正下方位置．但实际上,赤道上方200 m处无初速下落的小球将落在正下方位置偏东约6 cm处．这一现象可解释为,除重力外,由于地球自转,下落过程小球还受到一个水平向东的“力”,该“力”与竖直方向的速度大小成正比．现将小球从赤道地面竖直上抛,考虑对称性,上升过程该“力”水平向西,则小球

(A) 到最高点时,水平方向的加速度和速度均为0.

(B) 到最高点时,水平方向的加速度和速度均不为0.

(C) 落地点在抛出点东侧.

(D) 落地点在抛出点西侧.

解析:由题所给信息,根据对称性可知,现将小球从赤道地面竖直上抛,小球上升过程中,竖直方向小球的速度一直减小,由题知该“力”水平向西,且随竖直速度的减小而减小,由牛顿第二定律可知,小球的水平方向加速度减小,而水平速度初速度由0开始一直增大,上升到最高点时,小球的竖直速度为0,该“力”为0,水平加速度为0,水平速度达到了最大值,并不为0,所以选项(A)、(B)均错误;当小球向下运动过程中,该“力”水平向东,而水平速度向西,小球在水平方向将向西做减速运动,直到落地,所以整个过程中,小球一直向西运动,只能落在抛出点西侧,选项(C)错误,选项(D)正确．

无论从教的角度,还是从学的角度说,不仅要会做题,也要知道题中所蕴藏的物理本质和规律,从该题中还可提出很多问题．如,题目中的“力”是什么力?它的大小和方向是如何确定的?考虑地球自转影响时自由落体运动为什么会向东偏?竖直上抛落点为什么会向西偏?能否从中学物理知识范围推理出相同的结论?

1 地球转动对自由落体运动的影响

通常所说的自由落体运动是指物体只在重力作用下从静止开始的运动．这里对自由落体运动概念的理解有两个关键条件: (1) 是只在重力作用下,说明物体在运动中不受空气的阻力,也不能受其它力; (2) 是从静止开始的运动,即初速度为0．当自由释放点的高度不高时,物体所受的重力可看作是一个恒力,物体自由落体运动中的加速度是不变的,是一个匀变速运动;当不考虑地球自转的影响时,自由落体运动只能是一个匀变速直线运动．当释放点的高度较大,考虑地球自转影响时会是一个什么运动呢?

1.1 惯性参考系中的自由落体运动

图1

在赤道上物体释放点的正下方地面上建立一个随地球球心运动而不随地球转动的惯性坐标系,如图1甲所示.A为物体释放点B正下方地面上一点,由于地球的自转,人在地球上看到物体无初速度,其实是A、B两点的角速度相同,由v=ωr知,速度大小关系应是vB>vA,而且B点越高,A、B两点速度的差距就越大．在这样的坐标系中看,物体在水平方向上运动的速度大于地面上A点的速度,由于水平方向上物体不受力,小球并不是竖直落向地面正下方的A点,而是落向A点向东的一点,如图1乙中的A2点,此时地面上的A点随地球自转至图中A1点．显然,在这样的惯性参考系中,物体只受重力作用的条件能满足,牛顿运动定律也成立,但运动轨迹并不是直线,也不是传统意义下的自由落体运动．

设小球释放高度为H,地球的半径为R,地球自转的角速度为ω．释放时小球相对于空间坐标系的速度为vB=ω(R+H),A点的速度为vA=ωR,小球下落过程中,经时间t运动至图1乙的P处,相对于释放点B与地球球心O连线转过的角度为θ=ωt,由于θ角很小,sinθ≈θ=ωt,cosθ≈1,所以该处质量为m的小球所受的重力在x轴和y轴上的分力分别为Fx、Fy,由图2可得

Fx=-mgsinθ≈-mgωt，

Fy=-mgcosθ≈-mg.

由牛顿第二定律可求得小球在x轴和y轴上的加速度分别为

ax=-gωt，ay=-g.

(1)

对上式积分并考虑初始条件t=0,vx=ω(R+H),vy=0,得小球在x轴和y轴上的速度分别为

(2)

再对上式积分并考虑初始条件t=0,x=0,y=H,得小球在x轴和y轴上的速度分别为

(3)

地球上A点在t时间内转过的弧长为x1=ωRt,小球相对于地面的水平位移为

(4)

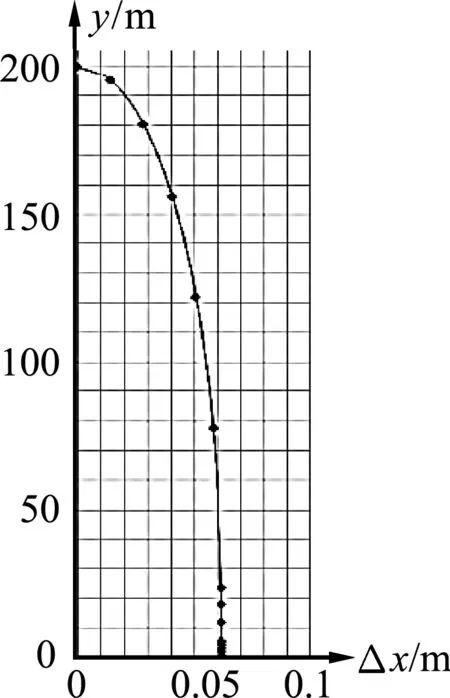
图3

应用Microsoft Excel编辑公式,计算0～6.39 s时间内对应于各时刻的Δx、y值,插入散点图如图3所示,即为小球该在惯性参考系中的运动轨迹．

Δx=x-ωRt=

(5)

小球自H=200 m处自由下落时,取g=9.78 m/s2代入上式得小球向东的偏移量约为Δx=6.2 cm．

1.2 随地球自转参考系中的自由落体运动

如果考虑地球自转影响时,地球是一非惯性系,物体在空中运动时,并不能直接应用牛顿运动定律．通过参考系的变换,如果在旋转参考系引入惯性力时,就可以应用牛顿运动定律处理动力学问题．

图4

小球自由落体运动中,小球在t时刻竖直方向的速度为vy=-gt,小球受水平向东的科里奥利力,如图4所示,其大小为F=2mωgt,其水平、竖直方向的加速度分别为

ax=2ωgt,ay=g.

(6)

对上式积分,并考虑初始条件:t=0,vx=0,vy=0，可得小球相对于地面的水平速度

vx=ωgt2,vy=gt.

(7)

对上式积分,并考虑初始条件:t=0,x=0,y=H,可得小球相对于地面的水平位移为

(8)

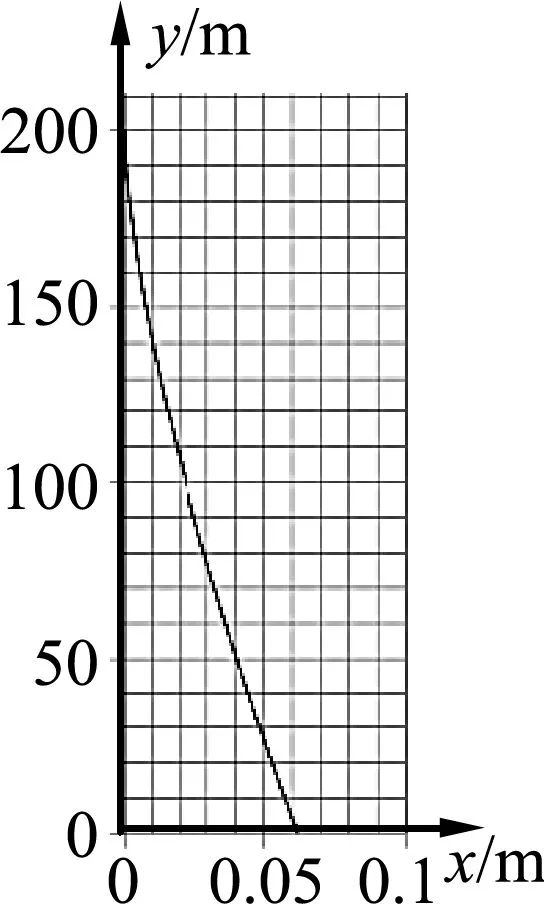
图5

应用Microsoft Excel编辑公式,计算0～6.39s时间内对应于各时刻的x、y值,插入散点图如图5所示,即为小球在该非惯性参考系中的运动轨迹．

(9)

将H=200 m,g=9.78 m/s2，ω=7.27×10-5rad/s代入上式，得Δx=6.2 cm．

对比(4)、(9)式可见,两种参考系中小球落地点与释放点的水平偏移量的表达式也相同,但观察到的运动轨迹是不同的,其中图5与我们观察的结果相同．

2 考虑地球自转影响的竖直上抛运动

2.1 惯性参考系中的竖直上抛运动

如图6所示,将小球自赤道地面上A点以v0的初速度竖直向上抛出,仅在地球引力作用下运动．以A点所在的空间点为原点,水平向东为x轴,竖直向上为y轴,建立如图6所示的平面直角坐标系(相对于地球球心不动,但不随地球转动)．若v0不太大时,小球运动时间t,至图7中的P处,相对于抛出点A与地球球心O连线转过的角度为θ=ωt,由于θ角很小,小球与地心连线转过的角度θ非常小,sinθ≈θ=ωt,cosθ≈1,所以该处质量为m的小球所受的重力在x轴和y轴上的分力分别为

图6

图7

Fx=-mgsinθ≈-mgωt，

(1)

Fy=-mgcosθ≈-mg.

(2)

由牛顿第二定律可求得小球在x轴和y轴上的加速度分别为

ax=-gωt,ay=-g.

(3)

对上式积分并考虑到初始条件:t=0,vx=ωR,vy=v0,可得到小球在x轴和y轴上的速度分别为

(4)

再对上式积分并考虑到初始条件:t=0,x=0,y=0,可得小球的位移分别为

(5)

地球上A点在t时间内转过的弧长为x1=ωRt,小球相对于地面的水平位移为

(6)

(7)

若v0=60 m/s,将ω=7.27×10-5rad/s,g=9.78 m/s2代入上式得小球的偏移量为Δx=-22 cm．

图8

可见小球落地点在抛出点西．

应用Microsoft Excel编辑公式,计算小球在运动时间内对应于各时刻的Δx、y值,插入散点图如图8所示,即为小球该在惯性参考系中的运动轨迹．

2.2 随地球自转参考系中的竖直上抛运动

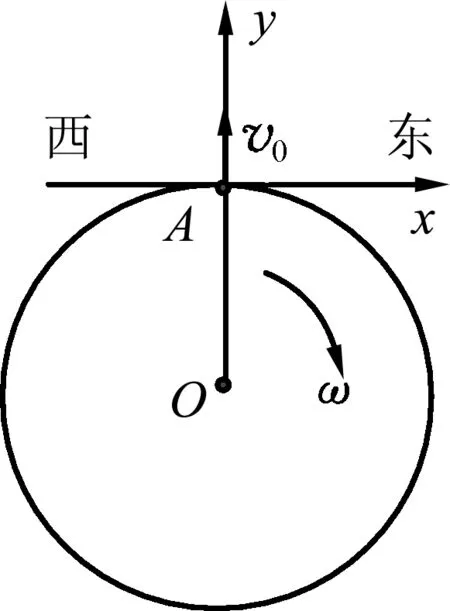
图9

小球竖直上抛运动中,竖直方向的速度大小为vy=v0-gt,可得到水平方向的科里奥利力为

F=-2mω(v0-gt).

(8)

水平方向和竖直方向的加速度分别为

ax=-2ω(v0-gt),ay=-g.

(9)

对上式积分并考虑初始条件:t=0,vx=0,vy=v0,可得小球相对于地面的水平速度和竖直速度分别为

vx=-2ωv0t+ωgt2,vx=v0-gt.

(10)

对上式积分并考虑初始条件:t=0,vx=0,vy=v0,可得小球相对于地面的水平位移分别为

(11)

(12)

将v0=60m/s,ω=7.27×10-5rad/s,g=9.78 m/s2代入上式得小球的偏移量为Δx=-22 cm．

图10

应用Microsoft Excel编辑公式,计算小球在运动时间内对应于各时刻的x、y值,插入散点图如图10所示,即为小球在该非惯性参考系中的运动轨迹．

可见,因地球自转角速度很小,当小球在离地球表面很近的空间运动时,在惯性参考系和随地球自转的非惯性参考系中,计算自由落体和竖直上抛落点和释放点的水平位移时都相同,都可以较准确地解释自由落体落点偏东,竖直上抛落点偏

西的现象,但在不同参考系中观察小球运动轨迹时差异是较大的,这是因为在运动时间内,随着地球的转动,观察者所在空间的上、下方位也会随地球的自转而旋转．

自由落体运动和竖直上抛是中学物理中两个重要的匀变速运动特例,本题源于经典,又进行了深化拓展．从中学阶段来说,并不要求学生学习地球参考系中的惯性力和科里奥利力,该题将科里奥利力进行了恰当阐述,没有点出力的名称,但说明了小球自由落体运动向东偏是由于该“力”而导致的,且说明了该“力”的大小和方向特点,学生只要应用牛顿第二定律等动力学知识,推理出该力在运动中的所起的作用,就会选出正确选项．该题的命题意图是以“落体偏东”现象为素材,系统深入地考查了考生对质点运动学相关概念和规律的深入理解和对称性思想的考查．该题设计新颖巧妙,着重考查了对知识的迁移能力,分析问题解决问题的能力．该题延续了近几年的命制思路和成功经验,体现了物理选择题第20题的特色:设置新情景,深化学科能力、回归学科本质,注重对学科思想方法的核心素养考查．