双行根数编目体系轨道误差研究∗

许晓丽熊永清

(1中国科学院紫金山天文台南京210008)

(2中国科学院空间目标与碎片观测重点实验室南京210008)

(3中国科学院大学北京100049)

1 引言

近年来,太空相撞事件时有发生,空间目标碰撞风险评估与预警规避成为人们关注和研究的热点.空间目标轨道数据(包括位置和精度)是进行碰撞风险评估的基础,只有掌握尽可能多和尽可能精确的空间目标轨道数据才可能得到准确有效的预警结果.

Chan、Akella、Patera等人利用碰撞概率对空间目标的碰撞风险进行描述,并研究了碰撞概率计算的一般方法[1−3],计算中交会目标的位置关系及它们的误差矩阵是非常重要的因素.碰撞概率的置信度在很大程度上依赖于空间目标的轨道精度.对于现阶段工程上普遍采用的10−4的概率阈值,交会距离为千米级甚至更小的交会事件,为确保概率计算的准确度,对轨道精度的要求在百米量级甚至更高.

美国从1957年第1颗人造卫星上天起,就开始进行空间目标的编目,随着空间目标的增加和探测能力的增强,编目数据库也不断增大.美国空间监视网(Space Surveillance Net,SSN)是目前世界上最先进的空间监视系统,对在轨目标进行编目维护,每天执行在轨目标的跟踪及轨道更新任务.北美防空司令部(North American Aerospace Defense Command,NORAD)将大部分空间目标的轨道信息以双行轨道根数(Two-Line Element,TLE)的形式在网上定期公布.TLE使用特定方法平滑掉了周期扰动项的平均轨道根数,为了保证轨道精度,必须采用与其相配套的Simplified General Perturbations 4(SGP4)/Simplified Deep-space Perturbations 4(SDP4)预报模型.

尽管利用编目轨道计算空间目标之间的碰撞概率并没有完全被航天工作者所接受,TLE数据仍然在当前的碰撞预警监视任务中发挥着重要作用.由于TLE数据中并未包含轨道误差信息,国内外众多学者对SGP4模型的精度进行了分析[4−10].Chan等[11]对比了地球静止轨道卫星通讯群的TLE预报结果和双站测距轨道确定系统的轨道预报结果,分析了TLE轨道精度随时间和空间的变化.文章指出TLE误差在不同区域表现出明显的系统偏差,并且偏差的大小和方向(正负)与地理经度加速度相关.Kelso[12]采用高精度的GPS精密轨道校验SGP4模型误差,分析了TLE数据的一致性.Flohrer等[13]将空间目标按照轨道特性分类,并统计分析各类目标精度随轨道特征的变化规律,其中统计的8000多个近地目标在沿迹方向的平均误差约为0.5 km.Bai等[14]指出目前一般采用的多项式拟合TLE轨道预报误差方法的不足,分析了预报误差随预报时间及轨道位置的周期性变化特征,并利用泊松系数进行拟合.韦栋等人设计了一套定轨方案,针对1000多个目标定量给出了SGP4/SDP4模型处理不同类型空间目标的定轨和预报精度,结果表明近地目标定轨精度为百米量级[15−16].

在碰撞概率计算中,空间目标的轨道误差采用轨道位置协方差矩阵来描述.协方差矩阵是在统计定轨过程中产生的一个概念,在定轨模型无误差的情况下,该矩阵取决于随机正态分布的观测资料,呈现3维正态分布.事实上定轨模型无误差是一种理想状态,很难得到保证,尤其针对精度并不高的编目轨道.如果轨道确定力学模型中有较大的长期项和周期项被忽略,即使跟踪观测资料呈全弧段分布,定轨过程还是不能完全准确地捕捉轨道运动的周期性和长期性演化规律.在定轨过程中,力学模型误差可以部分被解算参数所吸收,剩余的部分将导致编目轨道与真实轨道产生偏差.这种偏差除了观测资料引起的随机误差以外,可能还保留周期性和长期性的偏差,若存在,这种偏差显然是系统性的,统计定轨方法是无法估计的.这些系统误差的存在导致了编目轨道的精度不能再用状态协方差矩阵来完全描述,统计定轨过程中伴随产生的状态协方差矩阵失去了原来的意义,严重影响它的应用效果.

我们根据SGP4轨道预报模型的特点,首先在理论上分析了地球非球形引力田谐摄动项(主要是J22)对低轨卫星轨道精度的影响,结合仿真模拟的方法,研究了TLE编目轨道误差的系统特性,并讨论观测地点分布及观测弧段分布对轨道误差的影响.

2 理论分析

TLE是用特定方法平滑掉了周期扰动项的平均轨道根数,对于近地目标使用SGP4模型进行预报.SGP4是Cranford于1970年开发的,用于近地目标,模型中采用了Lane和Cranford 1969年的解析理论并进行了简化.SGP4模型为了确保较快的运算速度,采用了简化的受力模型,这导致TLE编目轨道的精度受到限制,其中地球引力场模型中只考虑了J2、J3、J4带谐项的影响,并未包含J22田谐项的影响.

地球非球形引力田谐摄动项对于低轨卫星的影响是2阶短周期效应[17],因而在人卫精密轨道确定和预报中(特别是对定轨精度要求不太高的情况下),往往容易被忽视.事实上,通过对地球非球形引力位田谐摄动函数展开,我们会发现其中包含与地球自转有关的项:

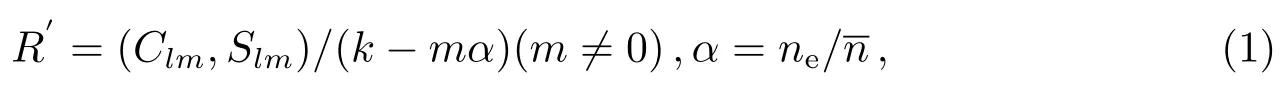
其中,k=0,±1,···,Clm和Slm为引力位展开的谐系数,和ne分别为卫星平运动角速度和地球自转角速度.展开式中包含k=0的项(地球自转项):

计算很容易发现:对于典型的102量级(归一化量纲)的定轨弧段和预报,由忽略田谐项产生的误差可以达到百米级甚至千米级.

3 仿真模拟

大部分空间目标的精确轨道是未知的,所以编目轨道的精度往往得不到正确评估,但我们可以采用仿真模拟的方法,利用精密定轨软件生成一条已知轨道,并模拟地面观测值,然后利用SGP4模型中采用的力学因素仿真TLE定轨,得到与TLE编目一致的轨道,这样就可以初步判断TLE编目轨道的误差.仿真中我们选取了轨道高度为500 km的近圆轨道作为目标,生成一条标称轨道.模拟观测数据进行轨道确定,最后与标称轨道比对获得残差数据.为了分析定轨误差的特性,我们利用10个随机种子数生成了10组随机误差并加入到模拟的观测数据中,这样通过定轨过程可生成10组轨道并与标称轨道比较可得出10组误差数据.具体仿真模拟过程如下:

(1)标称轨道生成 首先利用精密定轨软件生成一条标称轨道,采用的动力学模型包括70×70阶地球引力场、大气阻力(采用DTM模型)、第三体引力和太阳辐射压.初始历元根数如表1所示,表中a为轨道半长轴、e为偏心率、i为轨道倾角、Ω为升交点经度、ω为近地点幅角、M为平近点角.

表1 标称轨道的初始历元和轨道根数Table 1 Epoch and elements of the initial orbit

(2)观测数据模拟 利用互联网上的GPS测站坐标数据(北京、武汉、上海、昆明、乌鲁木齐、拉萨及西安)模拟生成4 d的观测数据,参照中国科学院空间碎片观测网现有的观测精度水平,模拟过程中给每个测站都加上5′′的随机测量差;

(3)观测数据定轨 采用与SGP4模型一致的动力学因素,利用模拟的观测数据进行轨道确定;

(4)轨道误差生成 利用观测数据定轨生成的轨道与标称轨道进行比较,它们之间的差异便可认为是定轨误差.

4 结果分析

4.1 力学模型对轨道误差的影响

首先根据SGP4模型的特点,在轨道确定过程中非球形引力场摄动也只考虑J2、J3、J4带谐项,而不考虑J22项等田谐摄动项,同时解算大气阻力因子来模拟SGP4模型中的B∗项,这样定轨生成的轨道和利用这批观测资料确定的TLE编目轨道基本一致,它与标称轨道比较就可以得出TLE编目轨道误差的特性,结果如图1所示.下面3个子图给出了U、N、W(沿迹方向、轨道内法向及轨道外法向)3个方向的轨道误差随时间的变化规律,可以看出U方向的误差最大,为了突出施加10组随机误差对定轨结果的影响,上方第1个子图对U方向的误差进行了局部放大.可以看出,10组轨道的误差数据基本重合(由于误差尺度较大,10组数据之间微小的差异并未体现出来),事实上通过计算发现10组数据之间在相同时刻的差异大部分处于分米级,增加随机误差模拟组数也不能改变这种差异,说明这些偏差是系统性的,不同时间有不同的系统差.从图1还可以看出:这次模拟中,编目轨道的最大系统误差在N方向最小,约为0.5 km,其次W方向的系统差可以达到0.8 km,而U方向的系统误差最大,在某些时刻可以达到1.8 km.另外在U方向误差放大图中我们还用纵轴为0的点标出了观测数据的时间分布,从图中可以看出在有观测数据的弧段,定轨系统误差较小,反之在没有观测数据的弧段,确定的轨道将会明显偏离真实的轨道.

图1 U、N、W方向轨道误差随时间的变化规律(定轨地球引力场模型考虑J2、J3、J4带谐项)Fig.1 Differences between the determined and true orbits in the U,N,and W directions when the J2,J3,and J4terms of zonal harmonics perturbation are used in orbit determination

为了解释图1中系统误差产生的原因,在定轨时非球形引力场摄动增加J22田谐项的影响,其他同前.结果如图2所示,U、N、W3个方向的轨道误差最大不超过2 m,并且10组数据基本上服从零均值的随机分布.对比图1和图2,它们之间的差异是由定轨模型中地球引力场中J22田谐项产生的,这也说明了TLE编目轨道中可能包含由于未考虑地球田谐项J22而产生较大的系统误差,量级甚至可能达到千米级.事实上,这里我们仅通过模拟考虑了地球引力场模型对编目定轨结果的影响.实际中,大气阻力是低轨卫星主要的摄动力,与高层大气密度的变化密切相关,但是高层大气密度的变化规律是非常复杂的,到目前为止人们也并未完全掌握其规律,只能采用高精度的大气模型来近似.如果考虑大气模型与实际大气的差异,编目定轨结果的误差分布将更加复杂.

图2U、N、W方向轨道误差随时间的变化规律(定轨地球引力场模型考虑J 2、J 3、J 4带谐项及J 22田谐项)Fig.2 Differences between the determined and true orbits in theU,N,andWdirections when the perturbation of the tesseral harmonicJ 2 2term is added

4.2 测站分布对轨道误差的影响

图1中的结果是我们通过模拟观测数据定轨得到的,而在实际的观测定轨中,测站地理分布情况、天气因素及可见条件等因素都将对定轨结果产生影响,而观测约束的不同也将改变系统误差的出现规律.

为了分析观测资料对轨道误差的约束作用,我们研究了不同的测站分布对编目轨道系统差的影响.相比之前,增加了19个国外观测站,它们的地理经纬度如表2所示.在地球平面展开图中粗略地标记出这些测站的位置,如图3所示.从图中可以看出,这些测站分布广泛,遍布了南北半球以及东西部地区,再加上国内的7个观测站组成了一个较为简单的全球观测网.

利用全球观测网生成的模拟测角数据进行定轨,定轨模型中的引力场模型仍只考虑J2、J3、J4带谐项的影响,定轨系统误差随时间变化曲线如图4所示.图中下方两条水平点线显示了模拟观测数据的分布情况,“∗”表示全球26个测站的观测时段,“+”表示国内7个测站的观测时段,可见由于“∗”对应全球布站,观测资料几乎均匀分布在整个定轨弧段,而对应的轨道系统误差相比仅用国内观测资料定轨结果的整体误差要小,最大误差由1.8 km降低为1.2 km.另一方面,虽然增加了测站,由于定轨力模型的限制,定轨结果仍旧存在较大的系统偏差,这也说明观测资料对轨道的约束不够强,不足以把确定的轨道拉回到真实的轨道,在某些时刻仍会较大地偏离真实值.实际上,若采用地理分布更广、几何构型更好的多个测站进行编目,定轨的精度将会有提高,但由于力学模型的限制,其提高的程度有限.美国拥有一个强大的地基观测网,其生成和发布的TLE编目轨道一定还有残余的系统差存在,国外一些学者的研究也表明了这一点[11,18].

表2 19个观测站的坐标位置Table 2 Locations of 19 new ground stations

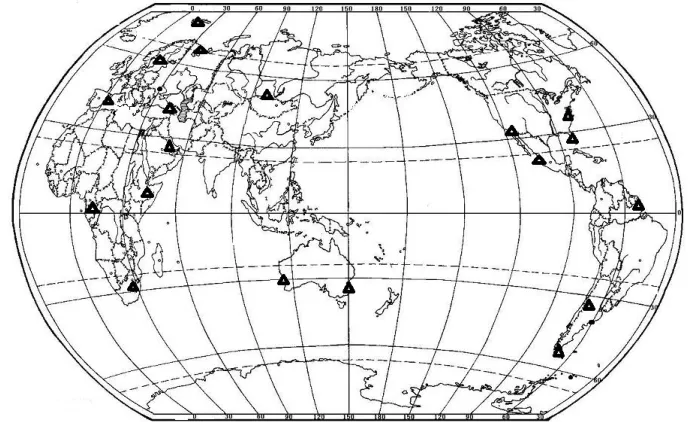
图3 19个观测站的分布情况Fig.3 Distribution of 19 ground stations

另外,在上面的定轨分析中都是利用计算机模拟的观测数据,资料产生的时间间隔及分布都是均匀的(每天有7个弧段,每个弧段大约10 min),而在日常实际的观测中,由于各种复杂因素的影响(天气、地理条件及观测仪器操作等),最终能够应用到定轨过程中的观测资料有限且分布不均匀,这也将影响最终的定轨精度.

图4 不同测站分布对定轨误差的影响.“∗”表示全球26个测站的观测数据,“+”表示国内7个测站的观测数据,实线表示全球26个测站的定轨误差,虚线表示国内7个测站的定轨误差Fig.4 Orbit errors with different ground stations.The symbol“∗” shows the observation data from 26 global stations,the symbol“+” shows the observation data from 7domestic stations,the solid line shows the orbit errors from 26 global stations,and the dotted line shows the orbit errors from 7domestic stations

5 结论

TLE编目轨道的SGP4力学模型中地球引力场只考虑J2、J3、J4带谐项的影响,并未包含J22田谐项的影响.本文在理论上分析了地球非球形引力位田谐项对低轨卫星定轨精度的影响,其中包含的地球自转项会使得摄动量级增大10倍.仿真模拟分析了编目定轨力学模型对定轨误差的影响,讨论了TLE编目轨道中系统误差的存在.对于轨道高度为500 km的近圆轨道空间目标,如果定轨力模型中未包含地球引力场J22田谐项的影响,将出现随时间周期变化的系统差,该系统误差甚至可以达到千米级,而且随测站和观测资料的分布而变化.一般来说,几何构型较好的测站分布在一定程度上可以削弱定轨中产生的系统误差,但由于力学模型的限制,无法彻底消除.本文对于工程实际中正确认识和使用TLE数据具有一定的帮助,对TLE编目轨道系统误差大小的判断还需要更加深入细致的工作.若设法将编目轨道中的系统误差和随机误差分离,并应用到空间目标碰撞预警中,将会提高碰撞风险评估的准确度.