采用高抛弹道的反临拦截器制导律设计
2018-08-24,,
,,
(西北工业大学 航天学院飞行控制研究所,西安 710072)
0 引言
随着临近空间高超声速巡航导弹、助推滑翔导弹和空间轨道机动平台等高超声速临近空间飞行器技术的大力发展,现有的防空反导体系将会面临着巨大的挑战[1]。对于临近空间高超声速飞行器,飞行速度快、突防能力强,具备一定的机动能力,给拦截带来了巨大的难题,目前尚缺乏有效的拦截策略和制导方法,必须针对高超声速临近空间飞行器开展特有的拦截策略和反临制导方法方面的探索[2]。
临近空间高超声速飞行器末段机动能力强,且轨迹无法预测,对其进行拦截难度较大,在巡航段受超燃冲压发动机的限制,高超声速飞行器机动能力较弱,因此最佳拦截段在临近空间高超声速飞行器的巡航段。为了对临近空间高超声速飞行器进行有效的拦截,国外实际上大量使用的拦截制导仍然以比例导引及其各种以比例导引为基础的改进型制导律为主。文献[1]通过对比比例导引律和微分对策制导律,可以看出在高超声速飞行器的拦截问题上比例导引制导律很难达到较高的制导精度要求。文献[2]研究了TBM拦截器的制导与控制问题,设计微分几何制导律,但是需要已知目标的运动信息;弧长域内的研究,需要转入时域方可实用化;制导曲率和挠率形式复杂等不足。文献[3]研究了动能拦截系统的拦截模式、导引头对目标的捕获概率、拦截机动目标的末制导律以及目标机动信息估计方法等问题。文献[4]研究了微分对策制导律,但是若对抗双方一方采取,一方不采取时,会因采取微分对策的一方过于保守,而使得微分对策导引的性能下降。同时,求解微分对策制导律要用极大值原理,需要解两点边值问题,难以在实际的拦截场景中应用。
本文以临近空间高超声速巡航飞行器为拦截对象,提出了采用高抛弹道拦截的设计思路,针对临近空间飞行器的弹道特征和机动性能,设计高抛弹道的复合制导律:初制导形成了一个初始抛射角,将拦截器抛射到较高的空域;中制导采用比例导引法,根据目标信息修正弹道倾角;末制导采用修正比例导引法,完成末端拦截的任务。为了保证各个制导律的平滑过渡进行了制导交接班的研究,本文提供了一个新思路利用高抛弹道进行拦截,并对目标不同机动模式的拦截效果进行分析验证。
1 问题的提出
由于拦截弹与高速飞行的目标相比,不再具有速度上的优势,因此,采用传统的攻击方式难以保证拦截的精度。拦截弹的速度一般小于目标的速度,势必会引起攻击区变得狭小,只能采用前向攻击的方式,而这种攻击方式对目标的机动较为敏感。另外,在前向攻击的拦截方式下,导弹和目标的相对速度更大,导致末制导时间很短;如果中制导结束时,误差较大,由于末制导时间较短,可能来不及消除初始误差的影响,或者消除误差所需的过载太大,这些都会导致脱靶量增大。
目前较为常用的导引律都是在比例导引律的基础上进行修正和完善。这些导引律都是基于导弹速度高于目标速度,导弹的机动能力远大于目标的机动能力这一前提下实现对目标的零脱靶量。在拦截过程中目标的速度变化和轨迹机动对导弹来说是一个小量,在导引律中基本没有考虑目标的加速度等运动信息。而对高超声速目标来说,拦截导弹已不再具有速度优势,且在临近空间拦截导弹的过载能力也大幅下降,经典的导引律已难以适应对高超声速目标精确拦截的需要。
通过创新地提出高抛弹道拦截的设计思路,预置抛射角能够有效的减小速度损伤,产生了更大的机动过载,有利于增加导引头的目标捕获,使得末制导阶段依然具有较高的速度,以便提供足够的气动力矩,减少攻击时间,能够在保持较远射程的情况下具有较小的弹体质量,从而实现精确拦截。
1.1 拦截问题的数学模型
临近空间飞行器由于所处的特定空域,且作为非合作目标,包括气动数据在内的很多飞行参数都是无法获得的,因此无法采用类似大气层外拦截的方法建立准确的目标运动模型,只能通过拦截器的导引头或数据链获取目标信息,包括目标当前时刻的位置、速度信息和跟踪滤波获得的加速度信息。本文选定的拦截对象为巡航式临近空间高超声速飞行器,采用乘波体气动外形,可利用临近空间的稀薄大气进行横向机动[3]。根据此类型飞行器的轨迹特性,并结合可探测的目标飞行器状态量,由于临近空间飞行器的飞行高度处于稀薄大气段,拦截器通常采用直接力控制方式,由载机发射到预定高度后,主发动机关机,拦截器仅受稀薄大气和推力矢量控制器的影响,整个拦截过程的动力学方程可描述为:
(1)

地面系弹目视线角速度:
(2)
2 导引律设计
由于反临作战中,拦截器飞行时间长,作战距离远,不同阶段拦截器获得的导引信息也不同,其导引律一般分为初、中、末三阶段制导的复合制导律。初制导依靠载机和数据链对目标探测,进行命中点预测,中制导使用自身惯导+数据链修正完成指令飞行,末制导依靠导引头捕获目标进行自寻的制导飞行[4]。
其中在本文中使用的是发射坐标系O-xyz,该坐标系的原点与发射点O固连。Ox轴在发射点水平面内并指向发射瞄准,方向,Oy轴垂直于发射水平面指向上方,Oz轴与其余两轴成右手坐标系,也叫做地面坐标系。
2.1 拦截器初制导律设计
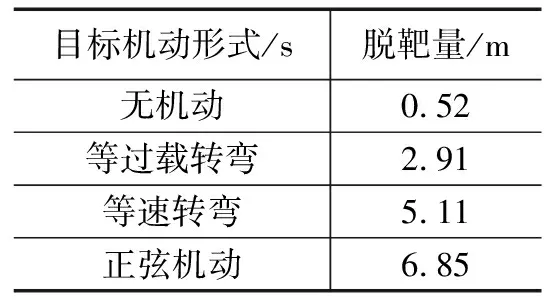
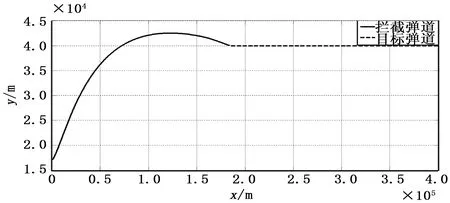
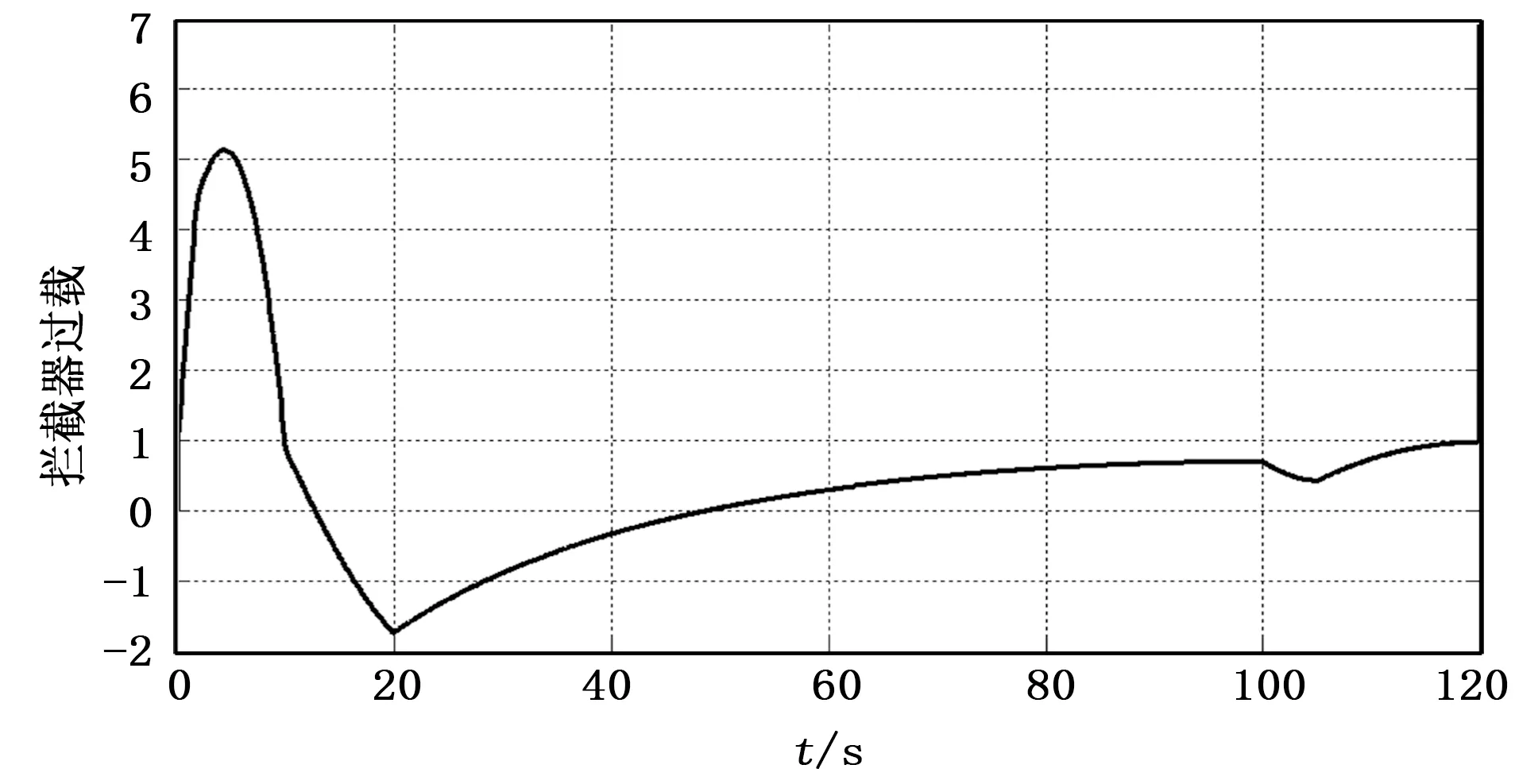
拦截器初制导采用程序控制,通过载机和数据链探测目标信息,并结合拦截器自身的飞行信息预测命中点,到初制导结束时刻t0控制拦截器达到指定的弹道倾角。t (3) 式中,t0为初制导时长,t为当前时刻,tlock为舵面锁定时间,θm和ψm分别为拦截器的弹道倾角和弹道偏角,θopt和ψopt分别为初制导中拦截器期望的弹道倾角和弹道偏角。 由于临近空间高超声速飞行器的飞行速度比拦截器快,所以拦截器一般采用前半球攻击的拦截策略,拦截过程的时长通常取决于拦截器与目标的x轴的水平距离,命中点在发射坐标系下的位置xg、yg、zg可采用下式进行估算[5]: (4) 式中,xT、yT、zT为目标在发射坐标系下的位置,texp为拦截器的预测飞行时间,θT、ψT分别为目标的弹道倾角和弹道偏角。 铅垂平面内高抛弹道的弹目相对运动关系如图1所示,为将拦截器抛射到较高的空域,期望的弹道倾角θopt可表示为在当前的视线角上预置一个抛射角θΔ的修正预置弹道倾角。 (5) 图1 拦截弹-目标铅垂平面弹道示意图 考虑到导弹需要飞行距离越远,抛射角度应该越大。因此,可以用下述公式估算抛射角: (6) 当texp<20 s时,导弹和目标距离很近,载机可能来不及将拦截器抛送到制定高度,因此不采用高抛弹道。对于参数k的选取,考虑到载机飞行高度越低,需要越大的预置角将拦截器送往预定高度,因此可将k用下式表示: (7) 式中,ymax表示拦截弹最大飞行高度。 初制导中拦截器期望的弹道偏角可取为拦截器与目标的侧向视线角: (8) 中制导在纵向和侧向采用比例导引法,制导律[6-7]可以表示为: (9) 式中,qz和qy分别表示纵向和侧向视线角,导航比选取为:k1=3,k2=3。 拦截器末制导采用修正比例导引法,为减小拦截器的需用过载,降低脱靶量,在其基础上引入拦截器速度变化和重力影响修正。 设修正项为p,则拦截器末制导律可表示为: (10) 式中,kf为末制导的导航比,对拦截器与目标纵向平面内的相对运动方程求导,得: (11) 将式(10)代入式(11),并定义N=kfgcos(qz-θ)整理后可得: (12) 将式(12)进行积分求解,并进行泰勒展开,可得: (13) 要求命中时刻拦截器法向过载不超过6 g,即t=tf时,ny=6,带入式(13)可求出修正项的表达式为: p= (14) 为保证不同阶段制导律之间的平滑过渡,避免制导律切换过程产生过载突变,在复合制导中需要考虑制导律的交班问题。由于初-中制导交班时,拦截器过载不会很大,因此初-中制导交班律采用满足一阶平滑的一次函数平滑算子进行过渡[8],一阶平滑过渡是指在衔接处保证两弹道速度方向一致,其核心思想是使加速度矢量连续。此时,交接班问题就转换为以两个常值矢量为始末点的两边值问题。在交接段导引头已经开始工作,而中制导段导引律仍然起作用,可以用这两种已知制导律为参量构造一个连续函数来作为交接班的制导规律,实现弹道的平滑过渡,基于以上思想,定义交接段导引规律即: (15) 零基交接强行要求在交接点弹道加速度为零,虽然它可以保证弹道平滑过渡。但这在交接段存在大的航向误差时会使拦截器在导引过渡段瞄准误差进一步增大,不利于拦截器命中目标。实际上在弹道交接点,使弹道加速度为零并无必要,其核心思想是使加速度矢量连续。这可以理解为使得交接班的加速度在交接开始时刻等于中制导结束时刻的加速度指令,则完成拦截器的中末制导交接班。此时,交接班问题就转换为以两个常值矢量为始末点的两边值问题。在交接段导引头已经开始工作,而中制导段导引律仍然起作用,可以用这两种已知制导律为参量构造一个连续函数来作为交接班的制导规律,实现弹道的平滑过渡。 对于中-末制导交接,由于拦截器已具有较大的速度和过载,为提高导弹命中精度,通常采用满足二阶平滑的三角函数平滑算子进行交接,二阶平滑过渡是指在过渡点保证两弹道的速度矢量与法向加速度方向都一致,其表达式为: a(t)=λ1amid(t)+λ2atrm(t) (16) 式中,atrm(t)为末制导指令加速度,λ1和λ2分别表示中制导和末制导的三角函数算子,其表达式为: (17) 本文根据X-51A飞行器的一些已知参数,并参考目前巡航式导弹的突防策略,设计了临近空间目标的3种典型运动模式,在发射坐标系下可表示为: 1)水平面匀速飞行: (18) 2)水平面等过载侧滑: (19) 3)水平面等过载爬升: (20) 式中,aT为目标加速度,φ为目标速度方向与瞄准线的夹角,即攻击进入角。 本节对本文提出的方法进行仿真验证,对于目标,分别考虑等过载转弯、等速转弯、正弦机动3种突防方式,并给出目标不同的机动时刻对脱靶量的影响。其中拦截器与目标相关参数如表1所示。 表1 拦截器与目标相关 表2给出了不同机动形式对拦截器脱靶量的影响。仿真结果表明,对于目标的等过载机动,拦截脱靶量较小,而对于目标进行等速转弯和正弦机动时,由于突防过程中目标过载持续变化,会产生较大的脱靶量。 表2 目标机动形式对脱靶量影响 表3给出了目标在命中前的不同时刻进行等速转弯机动,对拦截器脱靶量的影响。仿真结果表明,目标机动时距离拦截器越近,产生的脱靶量就会越大。 表3 目标机动时刻对脱靶量影响 图2给出目标进行等速转弯时,拦截器与目标的全段纵向弹道,图3拦截器与目标的全段侧向位置随时间变化曲线,图4为拦截器过载随时间变化曲线。 图2 拦截器-目标纵向平面弹道 图3 拦截器-目标侧向平面弹道 图4 拦截器过载 从图2可以看出,拦截器纵向平面的弹道近似抛物线,这种制导律可以使拦截器快速接近到目标的飞行空域,使导弹在末制导时有更大的过载用于应对目标的突防机动,图3可以看出,目标进行侧向机动,导弹同样能够进行有效拦截,图4可以看出拦截器在初制导和末制导的过载较大,其中最大过载出现在初制导段,中制导的过载很小,由于高抛弹道可以明显增大命中速度,减小飞行时间和脱靶量,因此在基于高抛弹道的制导律设计中,即使采用形式简单的比例导引法和修正比例导引法,依然能够对高超声速飞行器进行有效的拦截。 为获得临近空间飞行器的有效拦截方法,本文基于高抛弹道设计拦截器的初、中、末复合制导律,并分析目标不同机动形式和机动时刻对脱靶量的影响。仿真结果表明,这种制导方法能够对临近空间高超声速飞行器进行有效拦截,且制导律算法简单,有利于工程实现,为反临拦截制导方法提供了新的思路。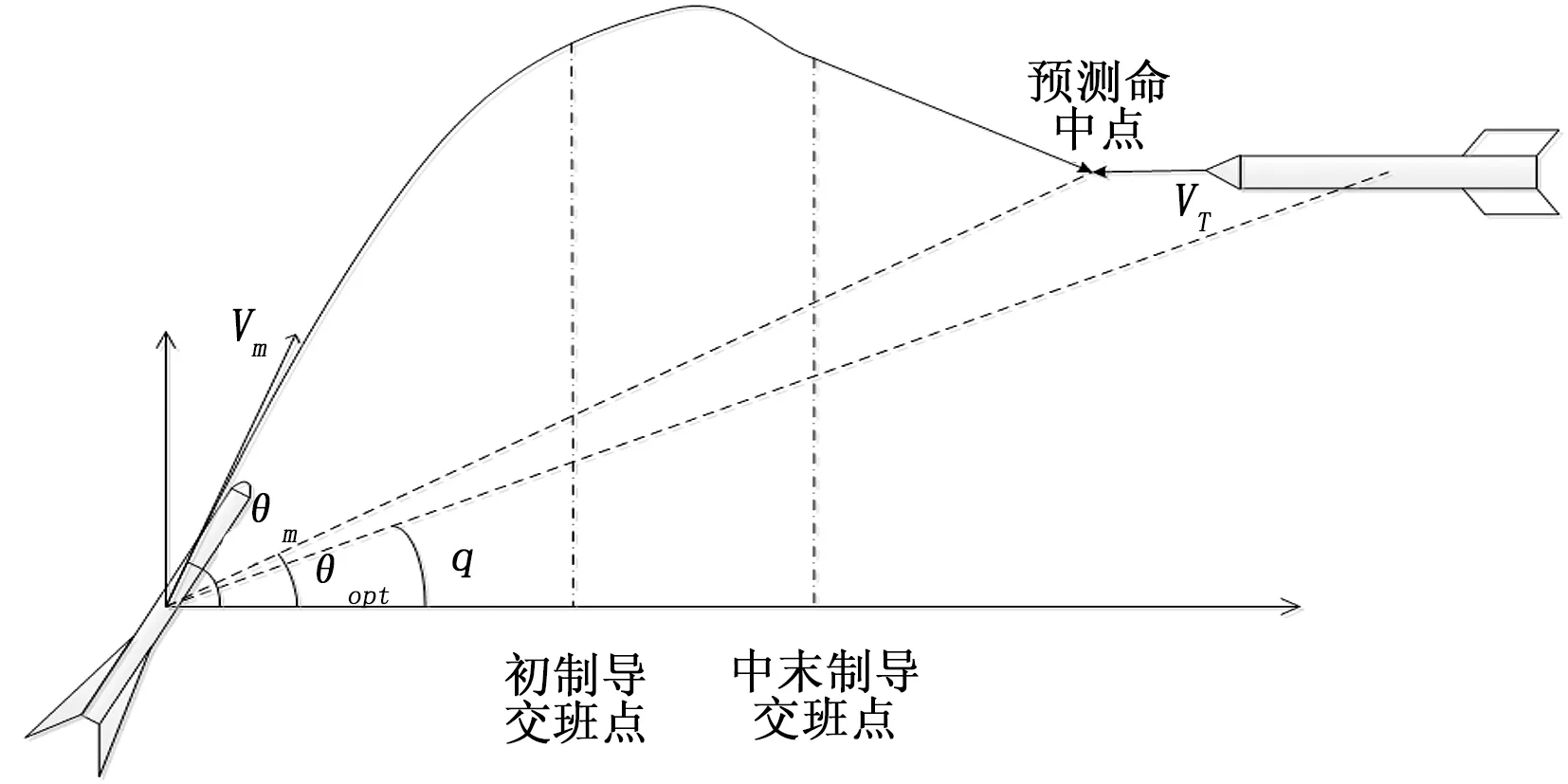
2.2 拦截器中制导律设计
2.3 拦截器末制导律设计
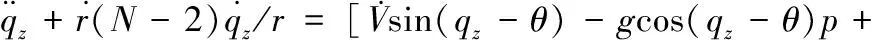
3 制导交班
4 仿真分析



5 结论
