选择合适的坐标系巧解一道静摩擦力问题

宋辉武

(鄂尔多斯市第一中学,内蒙古 鄂尔多斯 017010)

1 原题呈现

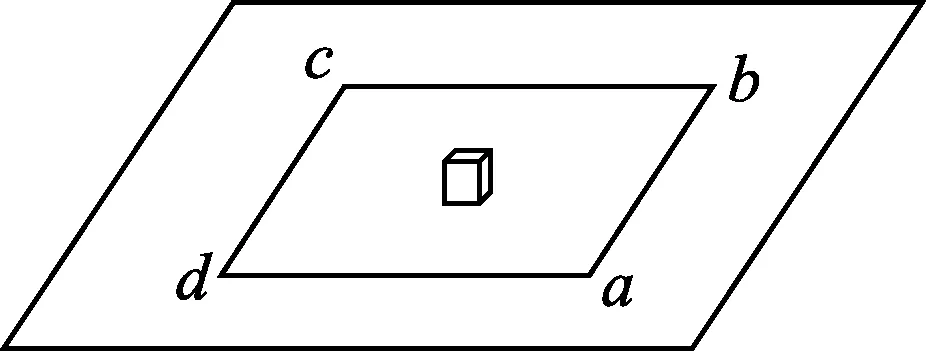
图1

例题.在水平桌面上放置一块正方形薄木板abcd,在木板的正中点放一个质量为m的木块,如图1所示,先以木板的dc边为轴,将木板缓慢向上转动,使木板的ad边与桌面的夹角为θ,再接着以木板的bc边为轴,将木板缓慢向上转动,使木板的dc边与桌面的夹角也为θ(bc边与桌面的夹角θ不变),在转动过程中木块在木板上没有滑动,则转动之后,木块受到的摩擦力大小为

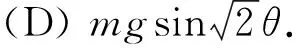
2 典型错解

3 选择合适的坐标系后简捷求解

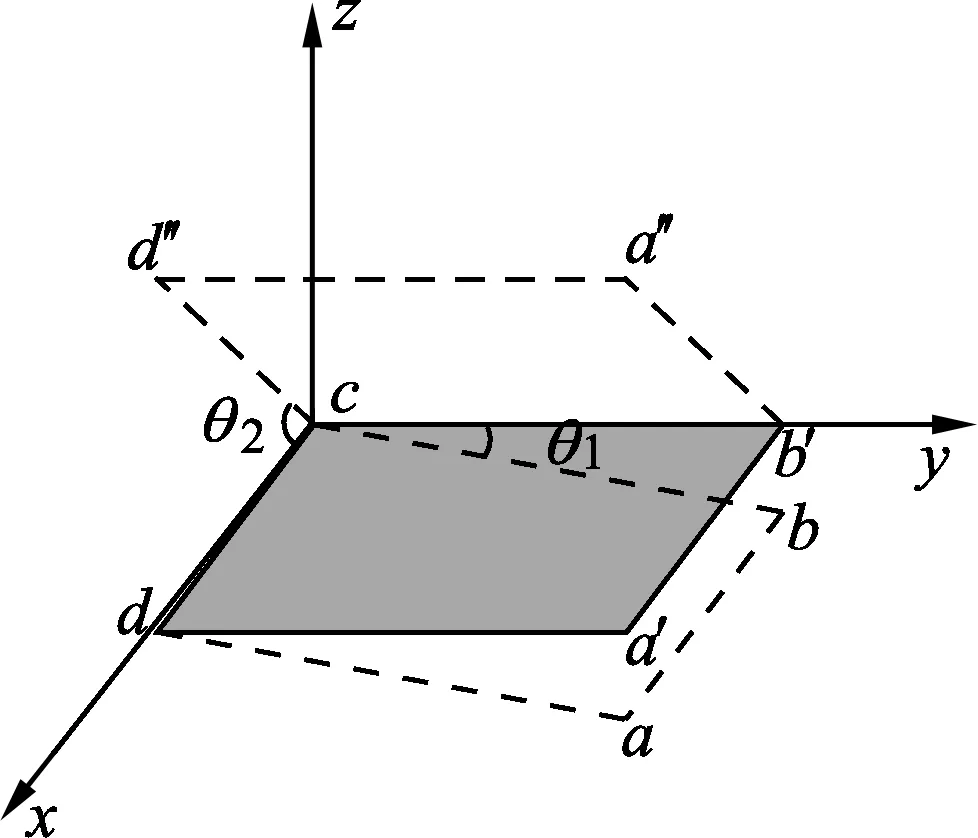
图2

该题的确是一道颇具难度的练习题,实际上我们只要求出两次转动之后的木板平面与转动前的平面之间的二面角即可,根据几何知识可以发现这个二面角又等于两个面的法向量的夹角.不妨设转动前的平面为平面1,转动1次后的平面为平面2,转动2次后的平面为平面3,也就是说,只需要利用数学方法求出平面1和平面3的法向量的夹角即可.不难发现,文献[1-3]是选择平面1来建立坐标系的,与已有文献不同,笔者选择平面2来建立坐标系,如图2所示.平面abcd为初始时的平面,即平面1,平面a′b′cd为第1次转动θ1后的平面(阴影部分),即平面2,平面a″b′cd″为第2次继续转动θ2后的平面,即平面3.以点c为原点建立空间直角坐标系,并且令平面2在xcy平面上.这样做的好处是,cb边刚好位于ycz平面上,且cb与y轴正方向的夹角为θ1,cd″边刚好位于xcz平面上,且cd″与x轴正方向的夹角为θ2．

这样一来,我们就很容易求得平面1和平面3内不在同一直线上的3点的位置坐标.设正方形薄板的边长为l,则平面1内的3个点的坐标为

c(0,0,0),d(l,0,0),b(0,lcosθ1,-lsinθ1).

平面2内的3个点的坐标为

c(0,0,0),d(l,0,0),b′(0,l,0).

平面3内的3个点的坐标为

c(0,0,0),b′(0,l,0),d″(lcosθ2,0,lsinθ2).

对于平面1来说,

cd=(l,0,0),cb=(0,lcosθ1,-lsinθ1),

因此其法向量

0i+l2sinθ1j+l2cosθ1k=(0,l2sinθ1,l2cosθ1),

其中i、j、k为x、y、z3个方向上的单位矢量,其中矢量用了加粗字体的方式加以区分.

对于平面3来说,

cd″=(lcosθ2,0,lsinθ2),cb′=(0,l,0)，

因此其法向量

-l2sinθ2i+0j+l2cosθ2k=(-l2sinθ2,0,l2cosθ2).

可得两个法向量的夹角α满足

cosθ1cosθ2．

因此木块受到的摩擦力为

当θ1=θ2=θ时,木块受到的摩擦力为

与文献[1-4]的结果是一致的．

4 结语

灵活地利用第一次转动后形成的平面2去建立空间直角坐标系,使得确定每一个平面所需要的3个点的坐标更加容易求解,不需要寻找复杂的空间几何关系.这是本文区别于已有文献解法的关键所在．