一种新型柔性电子回形包裹线结构应力应变分析*
2018-08-23李周平王龙飞
李周平,王龙飞
(陕西国防工业职业技术学院 数控工程系,陕西 西安 710300)
0 引 言
柔性电子技术近些年来发展迅速,可应用于环境监测、显示器以及人机交互性等方面[1],也可应用于碳纳米管[2-4]、无机半导体材料[5]、光电工程等[6]。CHIOLERIO A[7]和YIN Z P[8]研究了柔性电子产品的喷墨打印技术,包括将柔性设备应用于实际材料的问题;KHALEEL H R[9]和VYAS R[10]研究分析了柔性电子技术在天线方面的应用;文献[11-13]分析了在柔性聚合物基板上制造高性能低电压石墨场效应晶体管;LINZ T, KALLMAYER C等[14]在短袖上安装了一个灵活的电子测试模块来测量心电图(EKG)信号。
MACDONALD W A, LOONEY M K等[15]讨论了在电子应用中如何选择塑料材料,以及如何通过过程控制的例子增加最佳操作性能的关键问题;JAIN K, KLOSNER M等[16]介绍了一种新型的滚转式光刻系统,该系统的设计目的是解决分辨率、面板尺寸、工艺吞吐量、衬底变形、材料处理和产量等问题;CHEN Ying[17],MCALPINE M C[18]研究了纳米材料在柔性电子技术发展中的应用;JONG Y H, CHANG T H等[19]报告了一种高性能的柔性微波和数字电子产品,它消耗了在生物降解、可降解和可弯曲的纤维素纳米纤维纸上潜在的有毒物质;TOK J B H, BAO Zhe-nan等[20]总结了对柔性可伸缩电子、传感器和电源领域产生重要影响的几个重要结论;ZARDETTO V, BROWN T M等[21]在设备制造过程中通过一系列的测试来确定它们的光学、机械弹性、温度稳定性(电导率和变形);CHAN B D, HSIEH K H等[22]提出了一种用于制备微型有机柔性电极的转印冲压工艺,该工艺还可用于在介电/离子薄膜上制备电极,从而获得有机的柔性电容;CHEN X, HUTCHINSON J W[23]研究发现:在一系列柔性电子模型中,柔性基板上的人字形模型消耗了最小能量;文献[24-26]通过构建理论模型,来分析柔性电子结构的应力应变、剪应力和开裂应力等。
KIM S H, CHA H Y等[27]利用薄柔性印刷电路板作为一种电流收集器,以减少吸气式单极堆的体积,而被动空气呼吸作用下的定向效应几乎可以忽略不计;LI Shuang, LIU Xiao-li等[28]研究表明:剪切变形在柔性电子层和结构粘接层中占据了重要位置,而通过提出准确的分析模型,可以忽略正常的应变诱导变形;LEE Y, BAE S等[29]生产圆片形、高质量的石墨烯薄膜,通过金属层的瞬间蚀刻,将其传送到任意的基片上;HUANG Yong-an, YIN Zhou-ping等[30]通过热机械分析研究了3种不同柔性电子模型基底上的温度效应;SONG J, HUANG Y等[31]研究了一种非共面网格设计,可使电子系统在理论上和实验中达到可逆、大水平的弹力能力,并建立了一个力学模型来分析未知的物理量;SONG J[32], KHANG D Y[33]研究了柔性电子中一维、棋盘格状、有序人字形3种屈曲模型.
针对传统的柔性电子结构多是层和结构问题,本文将提出一种新型回形包裹线柔性电子结构。
1 模型与分析
柔性单晶硅材料在构建柔性硅基光电器件方面有着重要的基础作用,目前柔性单晶硅的制备方法主要有两种:薄化单晶硅材料和低维化硅材料方法[34]。
回形包裹线结构三维实体示意图如图1所示。

图1 柔性电子回形结构三维示意图
聚合物层将单晶硅区域包围在中间位置,以保证在受到外力冲击时,聚合物层保护单晶硅区域,使其不受干扰。包裹线一般承受横向剪切和弯曲负载。
柔性电子回形包裹线结构截面二维图如图2所示。

图2 柔性电子回形结构二维平面图
结构的几何中心设计在原点,因为回形结构是一个对称结构,因此本文只分析模型的上半部分。模型的几何尺寸为:h1=20 μm,h=40 μm,L1=25 μm,L2=50 μm,L=75 μm。PDMS系统的材料特性为:EPDMS=2 MPa,νPDMS=0.48。
根据经典力学建立各区域线性方程:
0
(1)
L1
(2)
L2
(3)
式中:x—横向坐标;z—横向坐标;u—x方向位移;w—z方向位移;θ—旋转角度;L—x方向长度;h—z方向高度;u,w,θ的第一个下标1、2、3—x方向的区域,0 在本文的后面部分,下标1、2、3具有相同的含义。 通过求导得到结构的轴向应变和剪切应变: 0 h1 (4) L1 h1 (5) L2 h1 (6) 式中:εx—轴向应变;γxz—剪切应变。 正应力和剪应力可以从梁变形理论的基本平衡方程推导,即: L1 h1 (8) L2 h1 (9) 式中:σx—正应力;τxz—剪应力;E1—单晶硅弹性模量;G1—单晶硅剪切模量;E2—聚合物弹性模量;G2—聚合物剪切模量。 根据虚功原理,可以得到: (10) 式中:δεx—结构的虚轴向应变;δγxz—结构的虚剪切应变;δw—结构z方向虚位移;q(x)—结构的外部载荷;b—结构的宽度。 将式(4,7)代入式(10),并进行分部积分,可以得到: (11) 式(11)中的力和力矩定义如下: (12) (13) (14) 式中:Mij(x)—结构不同区域受到的力;Qij(x)—结构不同区域受到的力矩;δθij(x)—虚旋转角度。(i,j=1,2,3) 令系数δθ11,δθ12,δw1,δθ21,δθ22,δw2,δθ31,δθ32,δw3为零,可以得到如下微分方程: (15) (16) (17) 将式(4~9)和式(12~14)代入式(15~17),可以得到: (18) (19) (20) 式(18~20)相关系数的表达式如下: (21) (22) (23) 为了便于求解计算,应对式(18~20)中的平衡方程进行积分计算。将边界条件代入式(21~23),求解其方程根,将得到的方程根代入式(4~6),就可以得到回形结构的应力/应变分布。 设定系统的边界条件如下: x=0:θ11(x)=0,θ12(x)=0,ω1(x)=0 x=L1:θ11=θ21,θ12=θ22,w1=w2,M11=M21, M12=M22,Q11=Q21 x=L2:θ21=θ31,θ22=θ32,w2=w3,M21=M31, M22=M32,Q21=Q31 (24) 因为qi(x)(i=1,2,3)等于零,因此式(18~20)中的平衡方程通过简化可以得到最终的精确解: α4x2+α5x+α6 θ12(x)=α1exp(λ1x)+α2exp(λ2x)+α3 (25) β4x2+β5x+β6 θ22(x)=β1exp(κ1x)+β2exp(κ2x)+β3 (26) φ4x2+φ5x+φ6 θ32(x)=φ1exp(η1x)+φ2exp(η2x)+φ3 (27) Aij,Bij,Cij可以从式(21~23)中得到,同时,αi,βi,φi(i=1~8)可以从式(24)的边界条件中得到。将式(25~27)代入式(4~9),便可得到结构的应力应变。 通过计算本文得到了回形包裹线结构应变分布的数值解,将其与有限元仿真得到的结果进行对比。 回形包裹线结构理论模型与有限元模型对比得到的应变曲线如图3所示(十字点图代表有限元模型得到的应变曲线,菱形线图代表理论模型得到的应变曲线)。 图3 PDMS系统不同位置处应变分布图 图3(a)显示:在x=16 μm处理论模型得到的应变曲线是一条依次增大的折线图,而有限元模型得到的结果是一条曲线图,接近于理论结果。在x=16 μm处材料均为PDMS聚合物,故有限元模型结果与理论计算结果契合度较高。 图3(b)显示:在x=36 μm处有限元模型和理论模型得到的结果图,在-20 图3(c)的结果与图3(b)的结果很接近,因为两者的位置信息采集点较近,一个信息采集点是x=36 μm,另一个信息采集点点是x=40 μm。 图3(d)显示:在x=63 μm处有限元模型和理论模型得到的结果图,在-40 通过图3的分析得知:中间区域的单晶硅区域,在外力作用下受到的应变最小,越靠近结构边缘,受到的应变越大。理论模型结果与有限元模型结果契合良好,且有相同的走向,因此证明了理论模型的正确性。 本研究建立了新型柔性电子回形包裹线结构的各个区域的线性方程,通过虚功原理得到了回形结构最终的应变解析解,再通过有限元软件建模分析,得到了结构应变的有限元解,通过二者的比较,验证了理论模型结构的正确性和合理性。结论如下: (1)基于材料力学知识建立了柔性电子回形包裹线结构的理论模型和基本方程; (2)柔性电子回形包裹线结构有限元模型结果与理论模型结果相比较,契合性好,有相同一致性和趋势; (3)提出了一种新的柔性电子回形包裹线结构理论模型,为柔性电子产品的生产、加工和设计提供了新的思路,这种新的回形包裹线结构可用于柔性电子结构的机械性能和稳定性的分析。 新的柔性电子回形包裹线结构为人们分析柔性电子结构的机械性能和材料性能提供了一个新的方向和视角,使得柔性电子技术的应用,由平面产品应用转向直线产品应用,并且使得微米级柔性电子线缆应用于电子产业成为可能。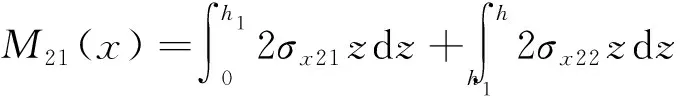



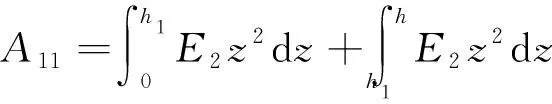
2 边界条件与解析
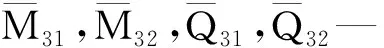
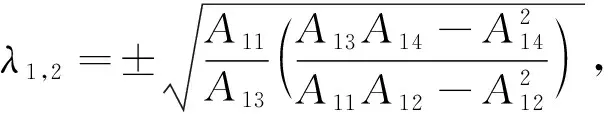
3 结果分析




4 结束语
