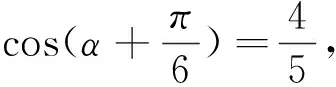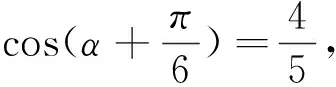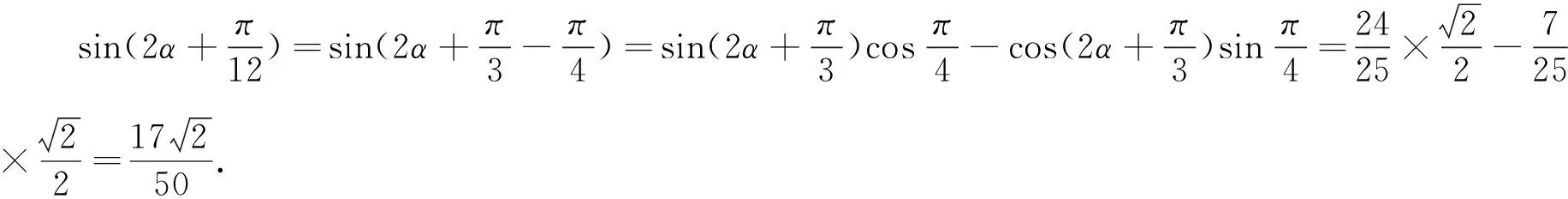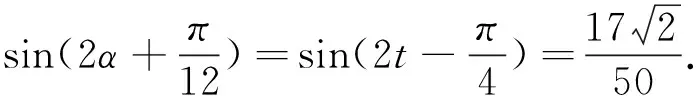换元法
——解题的利器
2018-08-23福建省古田县第一中学兰诗全林纪礼邮编352200
福建省古田县第一中学 兰诗全 林纪礼 (邮编:352200)
对于许多数学问题,若能多维视角适时进行转化,紧紧抓住题目中的数量关系及其结构特征,恰当运用换元法,不仅能使问题中各量之间的关系变得清晰明了,整体特征显现,沟通已知与所求,而且可使问题化难为易、化繁为简、化生为熟、化异为同,然后使问题顺利获解,现结合典型例子加以说明.
1 转化与换元相结合 将数学问题模型化
换元法是中学数学中最常用的方法与技巧之一,通过等价转化适时换元往往可以使繁难问题容易化、模型化,为数学问题解决找到根本方法.


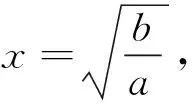
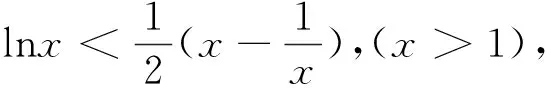
分析 分离参数a,可得a>g(θ),或a 解 令 sin2θ=2sinθcosθ=(sinθ+cosθ)2-1=x2-1. 反思 以上两例从表面上看,问题繁难、思路不清,通过仔细观察、等价转化、整体换元,将问题化生为熟、化难为易,找到根本的数学模型,从而揭开问题的本质特征,让题目轻松获解,其中换元起关键作用,真是“一桥飞架南北,天堑变通途”. 许多数学问题抽象不具体,解题切入点不明确,通过灵活适时换元,可以将抽象问题具体化、明确化,使思路从无序到有序,给解题带来生机与活力. 例3 设定义域为(0,+∞)的单调函数f(x),对∀x∈(0,+∞),都有f[f(x)-lnx]=e+1,若x0为方程f(x)-f′(x)=e的一个解,则x0可能存在的区间是( ) A.(0,1)B.(e-1,1)C.(0,e-1)D.(1,e) 解 设k=f(x)-lnx,则f(x)=lnx+k,所以由已知f(k)=e+1,又由f(x)=lnx+k,当x=k时,f(k)=lnk+k=e+1.因为f(x)是定义域为(0,+∞)的单调函数,所以k=e,则由上得 例4 若f(x)与g(x)都是定义在实数集R上的函数,且方程x-f[g(x)]=0有实数解,则g[f(x)]不可能是( ) 反思 以上问题抽象费解,应用换元法,步步为营,扎实推进,将问题具体化、明确化、实质化,顺水推舟,让数学问题层层揭开,不断深入,顺利获解.以上适时换元,构思巧妙、新颖独特、简捷有效,体悟以上解题过程,真有“精骛八极,神游四方”的数学思想方法在流淌. 许多数学问题陌生难解,可通过恰当换元,变换研究对象,将问题转换到新对象的知识背景中去研究,从而使非标准问题标准化,生疏问题熟悉化,给解题思维带上飞翔的“翅膀”. 例5 在约束条件x≥0,y≥0及3≤x+y≤5下,求函数u=x2-xy+y2的最大值和最小值. 解 令x=asin2θ,y=acos2θ,θ∈[0,2π],则3≤a≤5. 所以u=a2sin4θ-a2sin2θcos2θ+a2cos4θ =a2[(sin2θ+cos2θ)2-3sin2θcos2θ] 分析 椭圆内接三角形没有直接的面积公式,计算产生困难,怎么办?转换视角将椭圆内接三角形向圆的内接三角形转化是求解本题的好方法. 反思 例5通过换元将不等式转化为等式,为顺利解决问题铺平道路;例6通过换元将“椭圆内接三角形”转化为“圆的内接三角形”问题求解,实现化生为熟,化难为易,值得借鉴与学习,给人一种“春雨断桥人不渡,小舟撑出柳荫来”之感. 凑配法要有较强的观察力,要有较高水平的变形能力,对一些同学显得太“灵活”,有点捉摸不透.但通过换元法可使解题过程程序化、条理化、模式化,优化解题过程,让解题思路“有章可循、有法可依”. 则 解法1 (凑配法,略). 反思 明显,以上凑配法要有全局观,要有较强的内在观察力,要有几分“数学功底”才能应对自如,对能力不强的学生显得太技巧了,但换元法程序化,按步就班,无高难“动作”,既简约又简单,实为好法,值得深思悟透,定会感到“心有灵犀一点通”的和谐共鸣,应为全体同学所掌握. 以上数例说明许多数学问题通过换元,可使问题模式化、简单化、具体化、熟悉化、程序化,轻松快速地找到解决问题的突破口.最后本文旨在强调:“让换元成为一种习惯,让换元成为一种思想方法,让换元唤发无限的生机,让换元成为解题的利器”.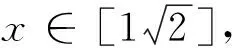
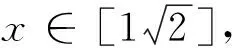
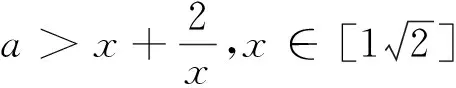
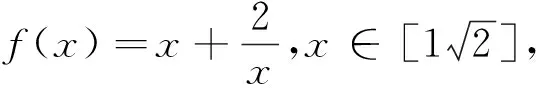
2 整体与换元相结合 将数学问题具体化


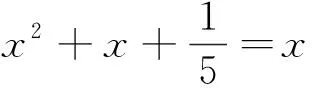
3 变换与换元相结合 将问题熟悉化


4 凑配法的本质是换元 换元凸显解题程序化