改进的遗传算法在机器人运动学中的应用

沈婷婷

（山东科技大学，山东 青岛 266590）

1 机械手简介

机械手主要由执行机构、驱动机构和控制系统三大部分组成。

2 建立模型

2.1 采取改进的遗传算法来优化机械手求逆解的问题

利用现有数据建立机械手运动模型：

式（1）为模型的目标函数。

2.2 根据模型的特点设计相应的遗传算法进行求解

（1）初始化群体。每个机械手运动的逆解采用如下方式计算和生成：

式中[ ]为取整函数；R为[0，1]内的随机数。

设置初始化进化代数为Gen=10。根据式（9）及式（10）生成一个初始种群作为第一代解。

（2）评价群体。

在本文中，适应度按如下公式计算：

（3）进行遗传操作。①选择。每次随机选取两个个体，分别计算其适应度，比较两个个体适应度大小，从中选出适应度大的那个作为新个体，重复操作，直到选出的个体等于种群大小为止；②交叉。在文中采用单点交叉来计算新个体的基因。如不满足，则重新选择个体进行交叉操作；

③变异。根据模型约束条件，把突变点的位置限制在第1位到第n-1位之间。

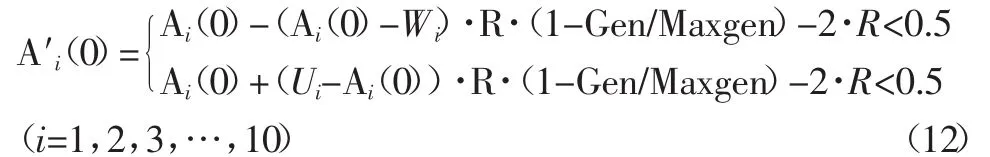
对完成交叉操作的个体，还需根据式（13）再进行变异操作，从而得到最新一代种群。

（4）终止。当Gen=Maxgen时，遗传算法终止；否则，Gen=Gen+1，转到第3步，继续循环。

2.3 MATLAB仿真结果

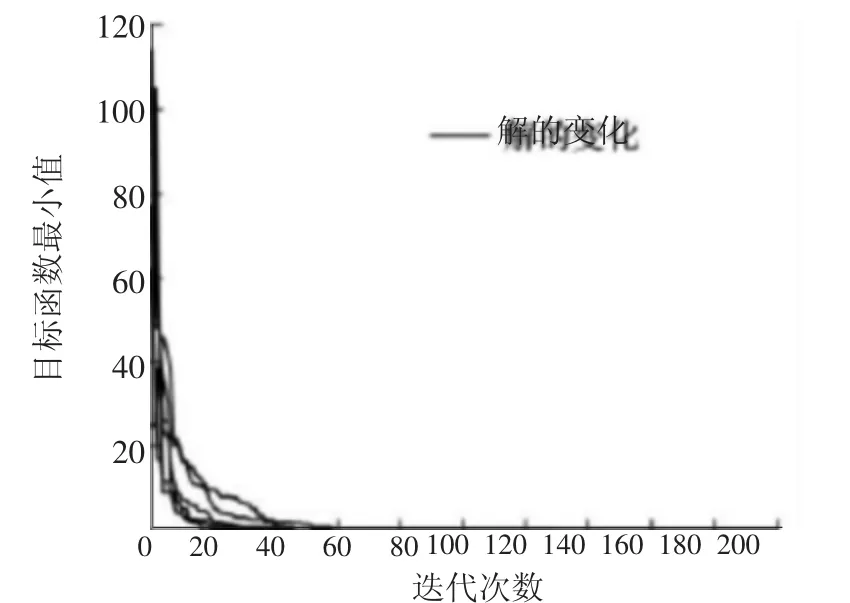
图1 MATLAB仿真结果

由仿真结果可以看到，改进后的遗传算法在进化到20代之前就已经基本上达到了最优解。

3 结语

针对平面关节型机器人的运动学进行建模分析，为了避免传统机器人求逆解方法的多解性、解的不存在性以及需多解的选取的缺点，本文采用了改进的遗传算法，算法的收敛速度更快，求解精度更高，稳定性更好。