旋转调制惯导用转位机构及高精度控制技术

彭惠，陈令刚，李燕生，薛庆全，李旬

(北京航天发射技术研究所，北京 100076)

0 引言

随着惯性导航技术的发展，旋转调制式捷联惯导技术得到了诸多应用与发展。该技术利用转位的方式可以将惯性器件的零偏对消进而可以有效提高导航系统精度[1-2]，已经在航海及地空导弹武器系统等领域得到了广泛的应用。

转位机构的控制到位精度会导致调制位置不对称，无法完全实现对惯性仪表常值漂移的调制平均作用[3]，从而难以完成旋转调制惯导系统的高精度对准要求和导航要求，对旋转调制式捷联惯导系统的对准和导航精度有着直接影响。高精度旋转调制惯导系统对转位机构的控制精度要求很高[4]。目前关于转位系统的控制方法包括PID(proportion integration differentiation)控制、神经网络及模糊控制等。文献[5]利用单一的速度环PID控制转位机构，这种方式实现简单，但是转位控制系统的抗扰动性较差，控制精度可能难以满足高精度旋转调制惯导系统对转位机构的控制精度需求。文献[6-8]中分别提出了利用神经网络原理、遗传算法和模糊控制算法调整PID控制参数，文献[9-10]中提出了单一参数的模糊PID复合控制思想，这些算法从理论上讲在某种程度上能够提高控制性能，但在实际工程应用中这些算法运算量相对较大增加了系统的复杂性，工程上难以实现。

针对上述问题，某型旋转调制惯导系统对转位机构的控制精度需求为10″，基于此需求，本文利用旋转变压器作为角度测量器件，直流力矩电机作为转位机构的执行元件，设计了一套转位机构，研发了电机位置、速率和电流三闭环PID控制器，同时增加前馈复合控制，实现对转位机构角度位置的控制，提高转位机构的控制精度。

1 转位机构组成

直流力矩电机响应快，力矩大且转速波动小，可以在堵转情况下长时间工作，机械特性和调节特性线性度好等优点。本文所设计的转位机构的机械台体设计成一个单轴转台，轴系由主轴、两对角接触轴承组成，轴上安装有直流力矩电机、旋转变压器等部件。旋转变压器作为测角度器件，采集旋转变压器输出并进行数字转换，将转换后的数字角度信号反馈到控制回路中实现对电机电枢电流及电机速度位置的实时高精度控制，转位机构的总体构成如图1所示。

如图1所示，控制系统分为位置控制环、速度控制环、电流控制环三环控制，采用前馈+PID的复合控制策略，同时在PID积分环节添加饱和校正，可实现对电机运行的角位置、角速率和电枢电流的精确控制。

1.1 角度信号采集

精确的角度采集系统是实现转位机构高精度控制的基础，旋转变压器的定子和转子各有2组空间上互成90°的绕组[11]。当在定子绕组上加上正弦激磁电压u=Usinωt后，转子上的正弦绕组和余弦绕组感应出电动势如下：

VA=Vmcosθsinωt,

(1)

VB=Vmsinθsinωt,

(2)

式中：Vm为零位处最大电压幅值；θ为转子转过的角度；ω为激磁电压频率。

采用精机的极对数为16的双通道旋转变压器，旋转变压器转动一圈，粗机转动一圈，精机转动16圈。即粗机旋转一圈转过360°，精机旋转一圈相当于转过22.5°。利用2片AD2S82A分别对旋变粗机和精机通道信号进行采集，由于粗机和精机的权位无法完全对齐[12],首先利用粗机及精机数据进行误差计算并判断，误差计算公式为

Δθ=C16-22.5i-J16,
i=C4-1,C4,C4+1,

(3)

式中：C16为粗机通道AD2S82采集到的16位数据；C4为C16的高4位数据；J16为精机通道AD2S82采集到的16位数据；Δθ为利用粗机和精机数据计算的角度误差。

旋变转过角度的选取方式为：依次计算i取C4-1,C4,C4+1计算角度误差Δθ，当Δθ<15°时，旋变角度θ为

θ=22.5i+J16, Δθ<15°.

(4)

利用所采集到的角度信号进行闭环反馈才能实现对转位机构的高精度控制。本文所采用的旋转变压器角度分辨率2″，能够满足使用要求。

1.2 转位机构控制系统设计

转位机构的控制系统主要是对直流力矩电机的控制，当给定位置输出精度时，控制系统能够快速响应并且在连续堵转时具有好的抗干扰性。本文采用角位置环、角速率环及电流环三闭环且增加速度前馈和加速度前馈的复合控制策略，控制系统总体结构如图2所示。

如图2所示，整个转位机构控制由串行422接口作为指令输入。当输入位置控制信号，信号首先输入位置环，位置环输出速度信号；速度环对输入速度信号进行PID调节，输出电机驱动参考电流，然后对电流作PID调节，通过PWM模块产生一路PWM占空比信号，经电机驱动芯片驱动转位机构转动。

采用PID复合速度前馈和加速度前馈的控制方法，即利用旋转变压器的角度微分及二次微分得到角速度信号和角加速度信号后，在位置环节的输出增加角速度和角加速度前馈后输入速度环进行速度环PID控制，加速度和速度的复合前馈能预测系统动态反应，能在一定程度上提高系统的响应速度。

2 转位机构控制算法

2.1 饱和校正PID控制器设计

传统的PID控制系统在饱和输出时积分环节往往还停留在一个比较大的值。本设计利用PID控制器经饱和环节后输出的值对积分环节进行校正，能使积分环节非常快地退饱和，其算法原理框图如图3所示。

具体算法如下：

e(k)=v(k)-v(k-1),

(5)

up(k)=kpe(k),

(6)

kc(U(k)-ub(k)),

(7)

ub(k)=ud(k)+up(k)+ui(k)，

(9)

其中：up(k)为比例项的输出值；kp为比例系数；e(k)为当前误差；Ti为积分系数，kc为积分项的饱和校正系数；ui(k)为积分项的输出值；ud(k)为微分项的值；ub为输出限幅前的值，Umax和Umin为输出限幅的最大值和最小值。

2.2 前馈复合控制器设计

位置环节输出增加速度和加速度前馈，其PID控制器输出需增加前馈量，即位置环的PID输出为

式中：θ为测角系统采集到的旋变角度；kvff为速度前馈系数；kaff为加速度前馈系数；Ub为纯饱和校正PID控制器的输出；Up为增加前馈复合的位置环输出控制量。

2.3 控制参数的整定

控制参数的整定遵循由内到外的原则，即先整定电流环参数，在电流环整定好的基础上整定速度环参数，最后整定位置环参数。

电流环采样及PID控制频率为10 kHz/s，即每4个PWM周期控制一次。电流控制器的参数整定的操作方法：给定一个频率为1 kHz的正反电流信号，对应速度环所给电流信号的速率；分别采集给定电流信号和反馈电流信号进行对比，反复尝试调整PID参数，直到效果最好为止，从而整定PID参数。

速度环和位置环的PID控制器控制频率为1 kHz/s，在电流环参数整定的基础上，首先给定一个速度信号，反复尝试调整速度环PID参数，直到效果最好为止。再在速度环参数整定好的基础上给定一个位置信号，调整位置环PID参数，最终使电机能快速、无超调地逼近目标角度位置。

3 数值仿真校验

Matlab 环境下的Simulink 仿真工具箱具有程序设计简单、直观，模型层次性强、封装性好、可移植性强等优点[13]，基于上述控制系统方案和算法，利用Simulink和M语言结合的方式实现对转位机构控制系统的仿真，使用该种仿真方案能与实际系统有较高的符合度。仿真中直流力矩电机伺服系统采用如下二阶数学模型[14-15]:

式中：Tm为电机时间常数；Te为电气时间常数；k为常数。

如图4所示，仿真系统分为位置环、速度环以及电流环。仿真模型的控制对象是直流力矩电机，本文所用直流力矩电机参数为：k=0.028 4，Tm=0.003 4,Te=0.001 1。

设定直流力矩电机初始角度为0°，目标角度为90°，限制电机最大转速为40 (°)/s，角度采样施加均值为0、幅值为0.000 1°的白噪声信号。电流采样环节施加均值为0、幅值为0.000 3 A的白噪声信号，系统采样计算周期为1 ms，仿真时间10 s。

位置跟踪曲线如图5所示, 图5b)是图5a)中曲线收敛时的放大图。角速率跟踪曲线如图6所示，图6b)是图6a)中曲线收敛时的放大图。

由图5可以看出，外环位置环实现了总体角位置无超调控制，稳态误差为0.000 2°(0.72″)。由图6可以看出，速度环可以有效地控制电机运行角速率，使之能快速、稳定地跟踪位置环给定的控制量，稳态误差为0.006 (°)/s，可以满足设计要求。

4 实物校验

某型号单轴旋转调制惯组设备的转位机构经过调试，控制参数如表1所示。

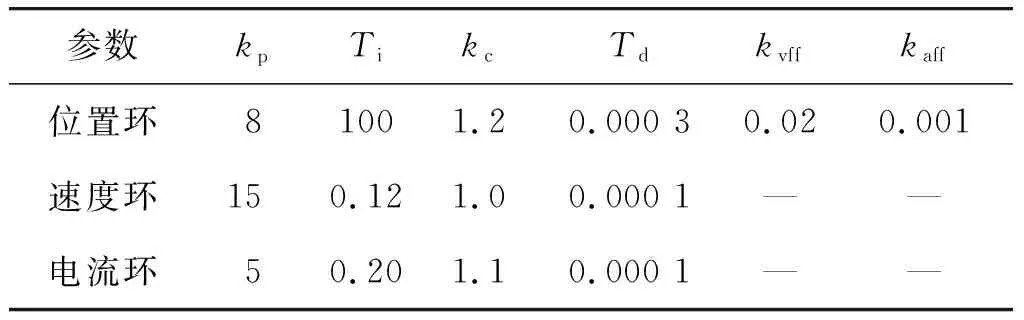
表1 控制参数表Table 1 Control parameters

实验室环境下将旋转调制惯组设备安装在固定基座上，上电控制转位机构初始锁定在0°位置，利用上位机给转位机构发送位置控制指令90°，180°和270°，采集转位机构角度数据和角速率数据，结果如图7所示。

图7中，第1行是角位置跟踪曲线，第2行是对应的角速率跟踪曲线，第3行是角位置跟踪收敛后的曲线。从图7中可以看出，控制系统对电机的位置控制精度可达到0.000 5°(1.8″)以内，与仿真结果相当。该实物校验结果是实验室静态环境下测得的，在外场环境试验时，受外界干扰影响，比如惯组设备装车后载车上的动态干扰，或者惯组设备架设在塔架上时，塔架受到风扰晃动对转位机构会造成一定的影响。本文所设计的转位机构已经经过多个型号的应用校验，其外场控制精度约在8″，满足设计指标要求。

此外，该种实物校验方法是假设转位机构的旋变采集角度系统无误差的基础上，而事实上任何一个测量系统都会存在误差。因此，后续工作中考虑改进测试和校验的方法，首先利用高精度的多齿分度台(精度可达0.1″或者0.01″)对角度测量系统进行标定，利用标定后的结果对输出的角度信号进行补偿，从而获取转位机构的绝对角位置控制精度。

5 结束语

本文提出了一种基于直流有刷力矩电机的简单有效的转位机构控制方法，阐述了基于旋转变压器的角度采集方法，设计了角度位置-角速率-电流三闭环积分改良型PID控制器和前馈复合数字伺服控制器实现对电机运行位置的无超调控制，搭建了基于Simulink的仿真平台，仿真结果表明位置环实现了角位置无超调控制且速度环可有效地控制电机速率使之快速稳定地跟踪控制量。虽然所阐述的实物校验方法是假定在角度采集无误差条件下进行，存在一定的不足之处。本文采用的旋变角度采集系统测角系统分辨率在1″，尚能满足现有指标要求，因此所述的转位机构控制精度校验方法仍然可认为是有效的。

目前，基于本文所介绍的控制方法的转位机构已经被成功应用于多个型号的单轴及双轴旋转调制惯组设备中去，使用效果良好，具有一定的工程应用和推广价值。